統計学2022
本ページについて
zoomオンライン会場への入室はpeatixからになります.視聴をクリックして入室してくださいまた待合室で登録者の確認をして入出許可しますので名前は「お名前@所属」にしてください
会場内ではカメラONでお願いします.また録音,録画,画面キャプチャ,撮影は禁止します.
上記を理解の上お申し込みください
なお,一般の方を含め(受講生の方も当然)チケット無料です
申し込みは以下のページから行ってください
https://medbbstat2022-02.peatix.com/
なお,申し込みにおいてPeatix Japan(株)のシステムにアカウントを持っていない方は作成することになりますが,アカウント作成の際に入力する情報については同社のポリシーに従うものとします.
この講義は,私の統計に関連する科目を受講している方を中心にに統計の入り口の部分について講義を行うものですが,
私の講義を受講されていない方でも,興味のある方はご参加ください.
開催内容および日時はpeatixでご確認ください
授業メニュー
統計学(1)尺度と度数と代表値
統計学(2)平均値の推定
統計学(1)尺度と度数と代表値と散布度
概要集団の状況を示す統計量や表,図について
統計に用いるデータ
基本どのようなデータでも統計処理は出来る出来ないのは,どのようなデータであっても一つしか存在しない時
データについて
レコード
症例,個体,被験者単位でまとめられたデータの塊.表の場合一行にその症例のすべてのデータを記していたらそれがレコード変数(変量)
データの項目名のことデータ
観測値や測定値のこと(数値)だけでなく性別など文字の場合もある.コンピュータ処理するとき,文字だと扱いにくい時があるのでその時は数字に置き換える(→コード変換)
例えば都道府県名であれば 北海道→01 青森県→02 奈良県→29
全国地方公共団体コードの上二桁=都道府県番号
|
<参考>全国地方公共団体コード(総務省) https://www.soumu.go.jp/denshijiti/code.html |
変量(データ)の分類
変量は様々なものがあるがそれらの性質をとりまとめ分類することが出来る。それぞれを尺度と呼び、4つに分類するのが一般的である
1分類尺度(名義尺度)
2順序尺度
3間隔尺度
4比尺度(比例)(比率)
1,2を質的変量(定性的)
3,4を量的変量(定量的)
性質としては上位互換性があり
4>3>2>1
統計量
取りまとめたものを「量で」示したもの.質的変数であっても度数(個数,人数など数えるもの)については「量」として示すことが出来る度数
どのようなデータでも度数を示すことは可能度数分布表
それぞれのデータ(変量)の数(出現頻度)をまとめたもの変量が名義尺度の時は多い順(お作法として。但しその他を出すなら一番最後)
順序尺度以降であれば順(名義尺度でも比較のためにお作法を破ることはある)
度数 ・・・出現頻度
相対度数・・・総出現頻度を1(100%)としたときのそのぞれの度数のしめる割合
累積度数・・・上位の変量の度数もあわせた度数
累積相対度数・・・累積度数の相対版
例題
1)以下の店名別のみかんの売り上げデータより度数分布表を作成せよ| 日付 | 店名 | 数量(箱) |
|---|---|---|
| 9月上期 | 奈良本店 | 1400 |
| 9月上期 | 大和郡山店 | 850 |
| 9月上期 | 生駒店 | 1200 |
| 9月上期 | 大和高田店 | 750 |
| 9月上期 | 五條店 | 800 |
| 9月下期 | 奈良本店 | 500 |
| 9月下期 | 大和郡山店 | 1250 |
| 9月下期 | 生駒店 | 1000 |
| 9月下期 | 大和高田店 | 1250 |
| 9月下期 | 五條店 | 1000 |
| 店名 | 度数 | 相対度数 | 累積度数 | 累積相対度数 |
|---|---|---|---|---|
| 1.00 | ||||
| 計 | 1.00 | ----- | ----- |
量的変数の度数分布表
量的変数の場合はその数値だけで度数を積み上げようにもなかなか上手くいかない場合がある.血圧 163.5mmHg 164.2mmHg 162.5mmHg・・・どれも度数を積み上げられない → 区間を設定する
|
「A~B」は「A以上B未満」と読む格好と思っていたが,分野などによって違うようです 「A以上B以下」のようにどちらの階級にも属してしまう可能性のある設定はしないように. |
| 階級 | 階級値 | 度数 | 相対度数 | 累積度数 | 累積相対度数 |
|---|---|---|---|---|---|
| 130~140 | 135 | ||||
| 140~150 | 145 | ||||
| 150~160 | 155 | ||||
| 160~170 | 165 | ||||
| 170~180 | 175 | ||||
| 計 | ----- | ----- |
度数分布図
質的変数・・・縦棒グラフ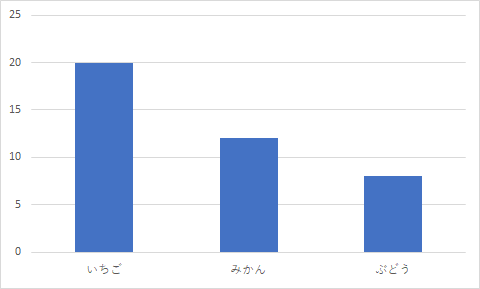
量的変数・・・ヒストグラム
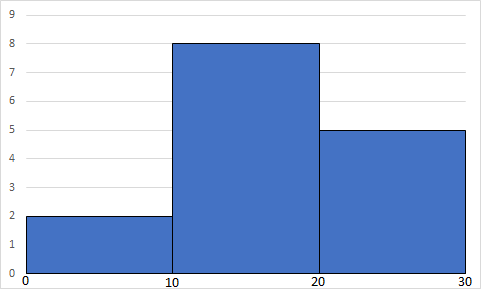
棒の間隔が無いのは値が連続している状態であるが故
普通の棒グラフは棒の長さが度数を示すが,ヒストグラムは棒の面積が度数を示す
| 「階級の幅を等しくすること」と説明している場合があるが,それは幅が変わると高さが変わる故で,実際にはそのような区間設定はよくある |
|
ヒストグラムーなるほど統計学園(総務省統計局) https://www.stat.go.jp/naruhodo/4_graph/shokyu/histogram.html |
受講者の皆様からの質問など
例題では名義尺度(店名)を用いて度数分布表を作成したが,名義尺度は計算できないのに計算して良かったのか?
度数そのものは,絶対的な原点(ゼロ点)を有しているので計算に用して大丈夫です店名は名義尺度ですが,ミカンの売り上げ数量(箱数)=(度数)は比尺度に相当しますので.
店名そのものは計算できない(例えば 奈良本店-五條店 という計算は出来ない)
記述統計量(代表値)
代表値と散布度からなる.←駅伝やマラソンの実況中継はこれらを利用しているから状況がわかる平均(Mean)
算術平均いわゆる割り勘.xbar=1/n(x1+x2+・・・+xn)
欠点:外れ値があると平均値は分布の中心位置を示さない(←それって代表的な値??)
→ 対処法:外れ値を取り除くか中央値を使うか
幾何平均(相乗平均)
全て掛け合わせて累乗根をとる
加重平均
重みづけ平均
例えば ミニテストと期末試験の平均をとる → そのままの平均で良いの?
度数分布表を用いた平均もこの方法・・・Σ(階級値×階級の度数)/n
中央値
昇順に並べたときに,真ん中の順番のデータ(変数)の値データの数が偶数だと真ん中のデータは二つになるのでそれらの平均値
最頻値
最も個数が多いデータの値最頻値は複数存在する場合がある→二峰性
平均値と中央値の考え方の違い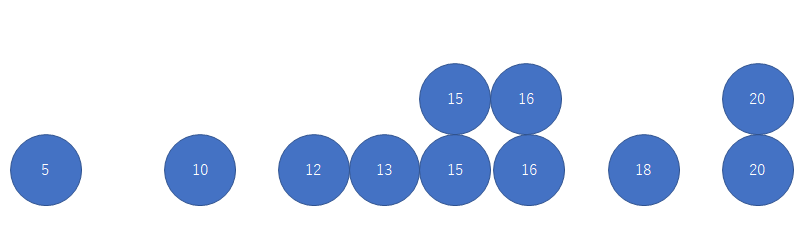 平均値(14.55) 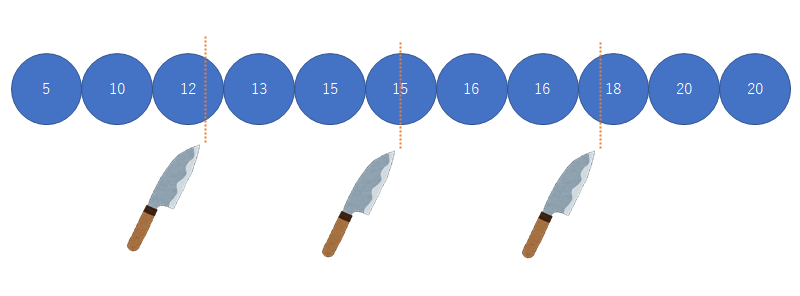 こちらは分布なんて関係なく中央値(15) データの分布に依存する(パラメトリック)=平均値 と データの分布に依存しない(ノンパラメトリック)=中央値,最頻値の関係がわかるかなと思います 例えば5が0に変わってしまうと平均値は大きく変わりますが,中央値は変わりません パラメトリック・・・数値に依存する(数値の分布によって値が影響を受ける)というとイメージしやすいのかな? |
記述統計量(散布度)
範囲
最大値と最小値の差四分位範囲
IQR=第3四分位数(75%点)-第1四分位数(25%点)(参考:中央値=第2四分位数(50%点))第3四分位数(75%点)の算出方法は数多くありまして・・・
|
一番わかりやすい四分位数の出し方は以下参照ください 実際には何種類か出し方があります. ダンゴ包丁理論(tukeyのヒンジ) https://medbb.hatenablog.com/entry/2020/12/12/091240 |
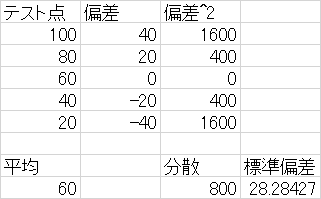
分散 標準偏差
範囲を用いた散布度と違い,平均値からのバラツキ(差=偏差)の平均を求めようというものただし偏差の平均をとれば集団内の各々のズレっぷりがわかると思って計算しても → 合計は常に0 故に平均も常に0
そこで偏差を二乗したものの平均を取っている → 分散
標準偏差は分散の正の平方根をとったもの
例題
以下の身長のデータより,度数分布表を10cmきざみの階級で作成したうえで,平均値(個票データ),平均値(度数分布表より加重平均),中央値,最頻値,範囲,分散,標準偏差を求めよ)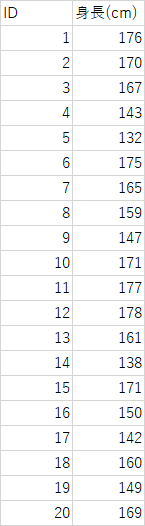
csvファイルはコチラをクリック
統計学(2)平均値の推定
概要集団全体(母集団)のデータを取得できない状況で,その一部(標本) がある場合,どのように推し量るのか?という話
説明のために用いたデータ
excelのRANDBETWEEN(110,140)をベースに一部調整したデータになります. 母集団は20000人からなり収縮期血圧を整数だけで記録される血圧計を用いた という想定です母数(母集団の統計量)ですが母平均は125.0 母分散は80.97です
|
そのため用いたデータはサイコロの目が均等にでるのと同様になります 以下のように今回の収縮期血圧データも110から140まで均等に出現しています. 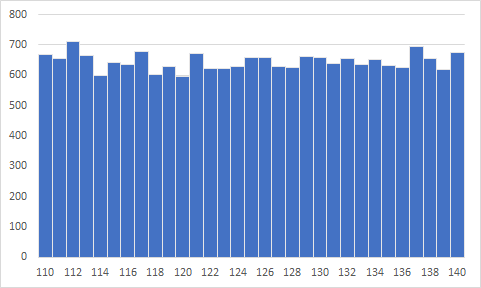 ただし,実際にある集団に対して収縮期血圧を測定するとその血圧データの分布はそのような形に(おそらく)なりません 諸々の事情を含めて設定したのですが実際とは異なる振る舞いをしているであろうことだけ承知しておいてください. 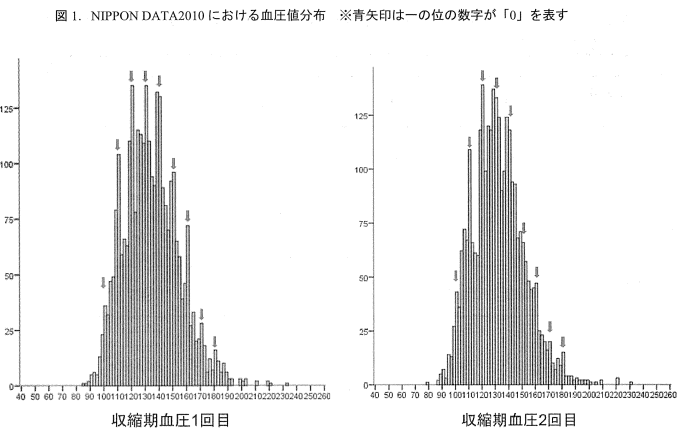 日本人の健康・栄養状態のモニタリングを目的とした国民健康・栄養調査のあり方に関する研究(厚生労働科学研究成果データベース)(https://mhlw-grants.niph.go.jp/project/23935)を加工して作成 <参考>日本人の健康・栄養状態のモニタリングを目的とした国民健康・栄養調査のあり方に関する研究(厚生労働科学研究成果データベース) https://mhlw-grants.niph.go.jp/project/23935 の平成24年度~26年度 総合研究報告書のP108図1の部分を取り出して加工したものが上記になります https://mhlw-grants.niph.go.jp/system/files/2014/143031/201412017B/201412017B0006.pdf |
標本より統計量を求めたもの(一部)は以下
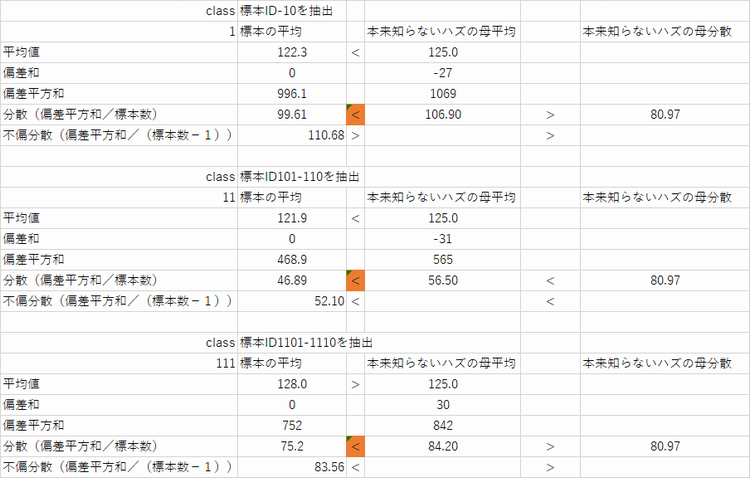
点推定
一つの数値(点)で推定値を示すこと欠点:推定値と真の値がどの程度ズレているのかよくわからない
利点:区間推定よりも簡単に算出できる
推定をしても必ず一致するわけでもない→せめて偏りなくバラついてほしい→不偏推定量
平均値
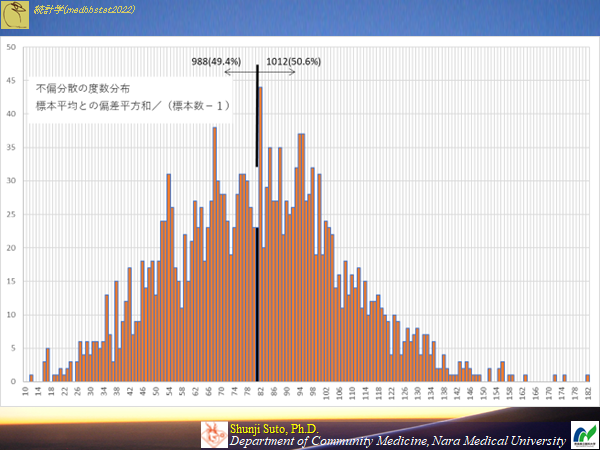
標本から求めた平均値は母集団の平均値の不偏推定量か?以下は20000のデータから標本数10の平均値を求めたもの(標本数2000)をヒストグラムにしたもの
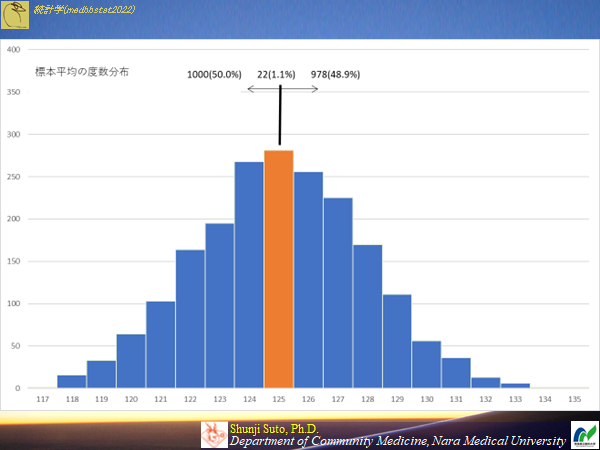
125.0未満の標本平均になった標本の数 1000(50.0%)
標本平均が125.0になった標本数 22(1.1%)
125.0を超えた標本平均になった標本の数978(48.9%)
分散
標本から求めた分散は母集団の分散の不偏推定量か?標本の分散
以下は20000のデータから標本毎に求めた平均(標本平均)を用いて分散を求めたもの(標本数2000)をヒストグラムにしたもの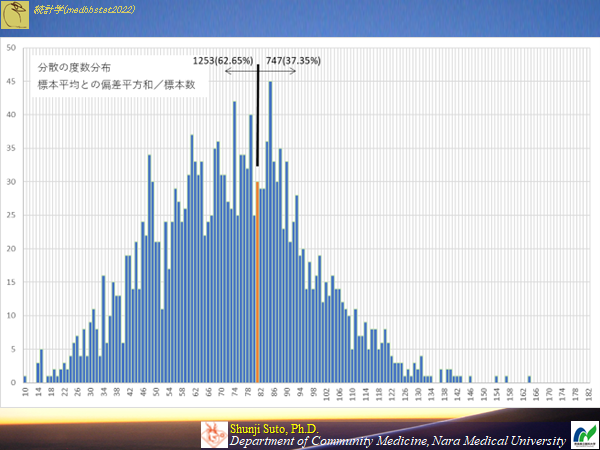
母分散の値よりも低く出る標本が多い→偏っている
母平均を用いた標本の分散
それでは母平均を用いて標本ごとの分散を求めると以下のようになる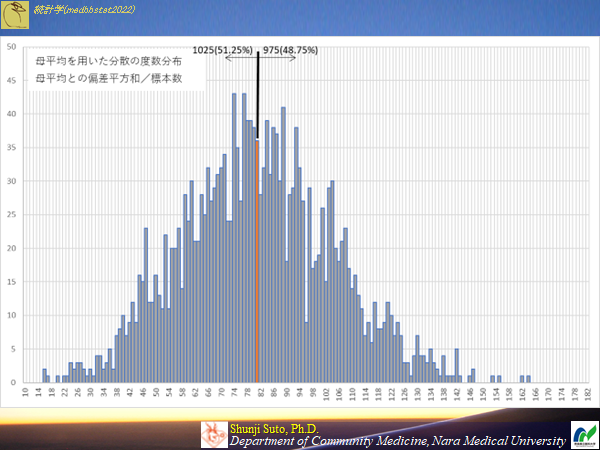
偏っていない推定が出来るが,そもそも母平均を用いることが出来るわけもなく・・・
不偏分散(標本の平均を用いて母分散の推定を行う)
|
<参考>不偏分散は何故nではなく(n-1)で除するのか(生物統計学2018奈良医大) https://medbb.net/education/nmubiostat2018/index.html#VAR |
今回のデータで検証すると
標本の平均を用いた分散<母平均を用いた分散 1978
標本の平均を用いた分散=母平均を用いた分散 22
標本の平均を用いた分散>母平均を用いた分散 0
ということで,標本平均を用いて母分散の推定を行うには,少し値を大きくしないといけない
上記の<参考は>母平均を用いた式を標本平均に置き換えて式を変化させた話 → 結論は偏差平方和を標本数nではなくn-1で除すると良い
標本平均の標準偏差=標準誤差
・標準偏差は標本の中でのそれぞれの値の分布のバラツキ具合を示したもの・標準誤差は標本の平均は標本ごとに異なるのでそのバラツキ具合を示したもの
2000の標本(n=10)より求めた平均値から分散を求めると8.01396
((((ID1~10の平均値)-125)^2)/10+(((ID11~20の平均値)-125)^2)/10+・・・+(((ID19991~20000の平均値)-125)^2)/10)/2000=8.01396
標本数は10,母分散は80.97なので母分散/標本数≒標本平均の分散
∴母標準偏差/√標本数≒標本平均の標準偏差
という関係があるように見える → 数式を展開するとそのような関係が導ける.以下参照
|
<参考>標準誤差SEはなぜ標準偏差σを√nで除するのか(生物統計学2018奈良医大) https://medbb.net/education/nmubiostat2018/index.html#SE |
例題
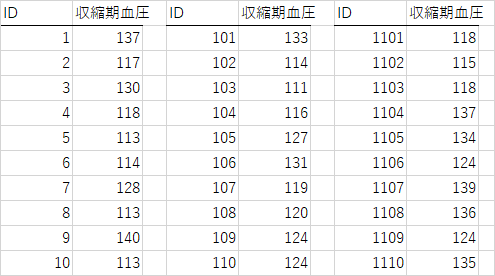
以下の3つの標本の個票データよりそれぞれの標本から母平均と母分散,標準偏差を点推定せよまた,それぞれの標本から求めた母平均と標準誤差(標準偏差より求めてください)の推定値を±した区間を求め,母平均(125.0)が含まれているか確認せよ
区間推定
点推定に幅をもたせたもの.幅の定義は確率(どの程度あたるものか)
∴100%あたる推定に意味は無い→確実に当たる幅を設定したら達成できるので
一般的に95%の確率で当たる区間(95%の信頼区間)で幅を決めている
平均値の区間推定については標準誤差を基準に計算する
正規分布
人など生物の成長に関わるものなどは、正規分布に近いとされている平均値に近い事象ほど多く起こり,平均値から離れていくほど少なくなっていく(どこまで離れていってもその事象は起こる)
標準正規分布表
正規分布は平均値を0とし,正規分布の広がりは分散に依存するので分散=1 つまり 標準偏差=1としたときに,平均値離れて行く程(Zがプラス方向に大きく マイナス方向に小さく)ズレることで出現確率が低下することを表わしたもの曲線下の面積=1(100%)
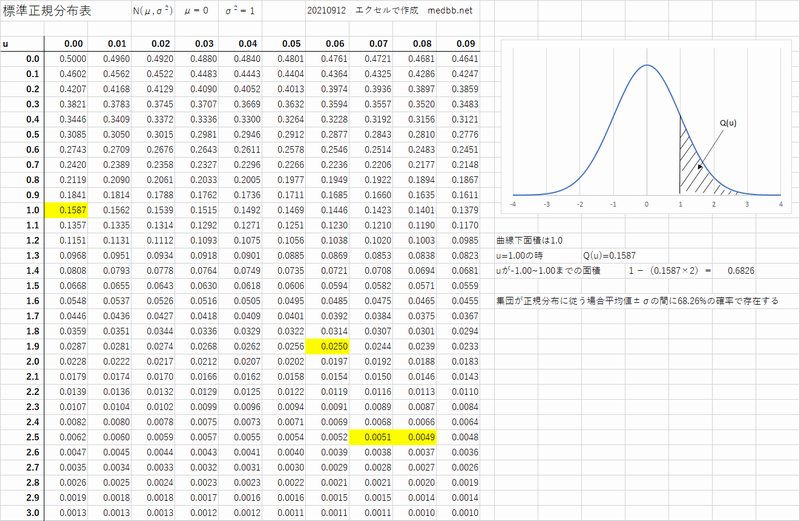
標準正規分布表のPDF版はコチラから
検証
母集団20000人からなる収縮期血圧を整数だけで記録される血圧計を用いて測定したデータの件20000のデータから標本数10の平均値を求めたもの(標本数2000)が,正規分布と同じような状況になっているか検証せよ
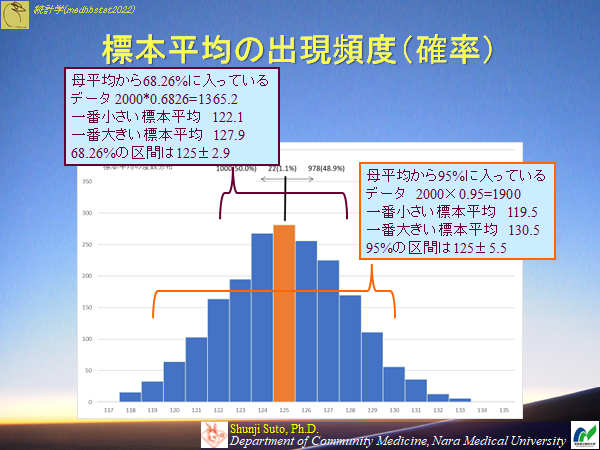


中心極限定理
血圧のデータは先に示した通り単純に乱数で発生させただけなので,サイコロと同様にどの血圧値も均等に出現しております.なので母集団のデータの分布は正規分布ではないのですが,母集団の分布によらず、抽出した標本の平均値は表本数が大きくなるほど近似的に正規分布に従うという性質があります.
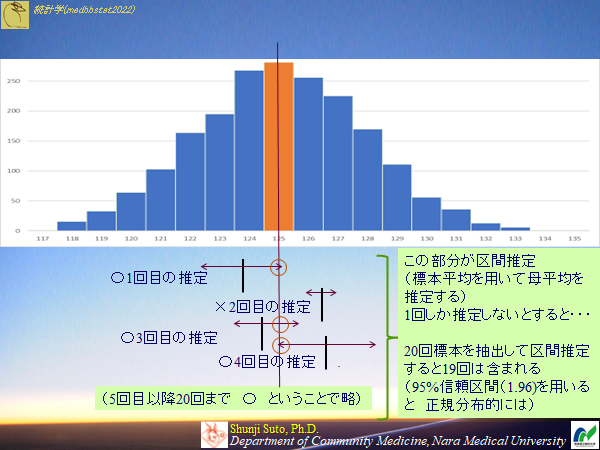
標本平均を用いた母平均の区間推定
いわゆる一般に行われる区間推定の話になります.検証したのはどなたも知るはずがない母数(母集団の平均値や母分散)を用いましたが,実際に標本からデータを取り平均値を推定する際に求めることが出来るのは,一つの標本から標本平均を求めることと不偏分散を求めるところまでです
そのため推定は標本のデータおよび正規分布を用いて95%の信頼区間を求めることで20回標本を抽出すれば19回は含まれるであろう区間推定を行うことになります.
例題
以下の個票データを用いて母平均を推定せよ.なお信頼区間は95%とし,正規分布を用いること
ちなみに95%の確率で(本来知る由もない)母平均を含むハズです.そのような結果になりましたでしょうか?(3つの標本ですので3つとも,もしくは少なくとも2つは125を区間に含んでいると思います)
(ところが2000の標本を全て計算して確認したところ残念ながら91.6%しか125を含みませんでした.ちなみに標本数を1000にすると95%(19/20標本)になりました.ここら辺のお話はまたの機会に)