Medbb.net

統計学２０２３

本ページについて

zoomオンライン会場への入室はpeatixからになります．視聴をクリックして入室してください

また待合室で登録者の確認をして入出許可しますので名前は「お名前@所属」にしてください
ニックネームがご希望の方は，peatixでその旨登録していただいたら，大丈夫です
会場内ではカメラONでお願いします．また録音，録画，画面キャプチャ，撮影は禁止します．
上記を理解の上お申し込みください
なお，一般の方を含め（受講生の方も当然）チケット無料です
なお，申し込みにおいてPeatix Japan(株)のシステムにアカウントを持っていない方は作成することになりますが，アカウント作成の際に入力する情報については同社のポリシーに従うものとします．

申し込みは以下のpeatixのページからよろしくお願いします
https://medbbstat2023.peatix.com
日程　タイトル
2023年12月10日(日)10時～12時 統計学(１)尺度と度数

2023年12月17日(日)10時～12時 統計学(２)代表値と散布度

2024年 1月 7日(日)10時～12時 統計学(３)母平均と母分散の点推定

2024年 1月14日(日)10時～12時 統計学(４)母平均の区間推定

12月の初旬の日曜日午前中を使って記述統計
1月の初旬の日曜日の午前中を使って平均値の推定を行います
本シリーズは検定の話の手前までですが，推定の話をしっかり理解すれば検定の話は理解しやすくなるかと思います

この講義は，私の講義（後期配当科目）で統計に関連する科目を受講している方を中心にに統計の入り口の部分についてフォローする目的で行うものですが，
私の講義を受講されていない方でも，興味のある方にご参加いただけたら幸いです．

授業メニュー
統計学（１）尺度と度数

統計学（２）代表値と散布度

統計学（３）母平均と母分散の点推定

統計学（４）母平均の区間推定

統計学（１）尺度と度数

概要
集団の状況を示す統計量や表，図について

統計に用いるデータ

記号によってあらわすことが出来る状態であることが前提．
基本どのようなデータでも統計処理は出来る
出来ないのは，どのようなデータであっても一つしか存在しない時

データについて

レコード

症例，個体，被験者単位でまとめられたデータの塊．表の場合一行にその症例のすべてのデータを記していたらそれがレコード

変数（変量）

データの項目名のこと

データ

観測値や測定値のこと（数値）だけでなく性別など文字の場合もある．
コンピュータ処理するとき，文字だと扱いにくい時があるのでその時は数字に置き換える（→コード変換）
例えば都道府県名であれば　北海道→０１　青森県→０２　奈良県→２９
全国地方公共団体コードの上二桁＝都道府県番号

＜参考＞全国地方公共団体コード（総務省） https://www.soumu.go.jp/denshijiti/code.html

都道府県番号に順列は存在しない．一方，文字で順列の存在するもの（松　竹　梅）はその法則にしたがった番号を振ることがあるので注意

変量(データ)の分類

変量は様々なものがあるがそれらの性質をとりまとめ分類することが出来る。
それぞれを尺度と呼び、4つに分類するのが一般的である
１分類尺度（名義尺度）
２順序尺度
３間隔尺度
４比尺度（比例）（比率）

１，２を質的変量（定性的）
文字，数字，符号，文字記号，数値記号・・・
３，４を量的変量（定量的）
　数値（数字），数値記号，単位記号
性質としては上位互換性がある
４＞３＞２＞１

例題１－１）

以下の文章中の下線部の尺度を示せ
折角の日曜日，天気も晴なので車に乗ってイオン橿原店までドライブ．
昼食はマクドナルドでチーズバーガーとポテト，LサイズにするかMにするかで悩む
昼食後車を走らせるがガソリンが少ないので35リットルほど給油．
無事目的地に到着し駐車場から外に出るとなにやら少し寒い，確かに気温を見ると１２℃と先程よりも低い
なので上着を買って帰ることにした．丁度バーゲンセールをやっている．値段は３９８０円，凄く良いものを買うことが出来ました．

統計量

取りまとめたものを「量で」示したもの．質的変数であっても度数（個数，人数など数えるもの）については「量」として示すことが出来る

度数

どのようなデータでも度数を示すことは可能

度数分布表

それぞれのデータ（変量）の数（出現頻度）をまとめたもの
変量が名義尺度の時は多い順（お作法として。但しその他を出すなら一番最後）
順序尺度以降であれば順（名義尺度でも比較のためにお作法を破ることはある）
度数　　・・・出現頻度
相対度数・・・総出現頻度を1（100%）としたときのそのぞれの度数のしめる割合
累積度数・・・上位の変量の度数もあわせた度数
累積相対度数・・・累積度数の相対版

例題１－２）

以下の店名別のみかんの売り上げデータより度数分布表を作成せよ

日付	店名	数量（箱）
9月1日	奈良本店	１４００
9月1日	大和郡山店	７００
9月1日	大和高田店	４５０
9月2日	奈良本店	１０００
9月2日	大和郡山店	９００
9月2日	大和高田店	１１００
9月3日	奈良本店	１６００
9月3日	大和郡山店	４００
9月3日	大和高田店	８５０

店名	度数	相対度数	累積度数	累積相対度数
計		１．００	-----	-----

量的変数の度数分布表

量的変数の場合はその数値だけで度数を積み上げようにもなかなか上手くいかない場合がある．
血圧　163.5mmHg　164.2mmHg　162.5mmHg・・・どれも度数を積み上げられない　→　区間を設定する

「A～B」は「A以上B未満」と読む格好と思っていたが，分野などによって違うようです 「A以上B以下」のようにどちらの階級にも属してしまう可能性のある設定はしないように．

階級	階級値	度数	相対度数	累積度数	累積相対度数
130～140	135
140～150	145
150～160	155
160～170	165
170～180	175
計			-----	-----

度数分布図

質的変数・・・縦棒グラフ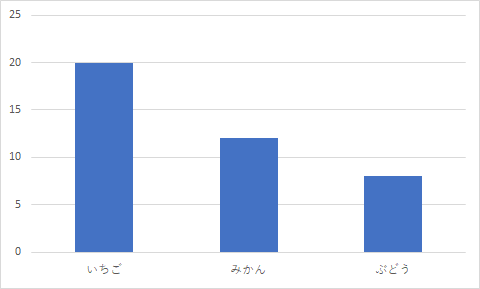

量的変数・・・ヒストグラム

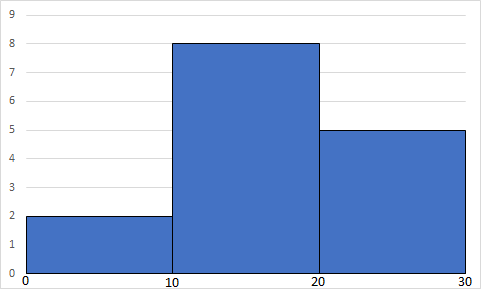
棒の間隔が無いのは値が連続している状態であるが故
普通の棒グラフは棒の長さが度数を示すが，ヒストグラムは棒の面積が度数を示す

「階級の幅を等しくすること」と説明している場合があるが，それは幅が変わると高さが変わる故で，実際にはそのような区間設定はよくある

以下の参考資料に区間幅の異なるヒストグラムについても説明なされているのでよろしければごらんください

ヒストグラムーなるほど統計学園（総務省統計局） https://www.stat.go.jp/naruhodo/4_graph/shokyu/histogram.html

例題１－３）

あるクラスの生徒の身長を計測したところ以下のような結果が得られた．度数分布表および度数分布図を作成せよ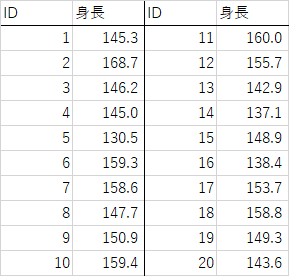

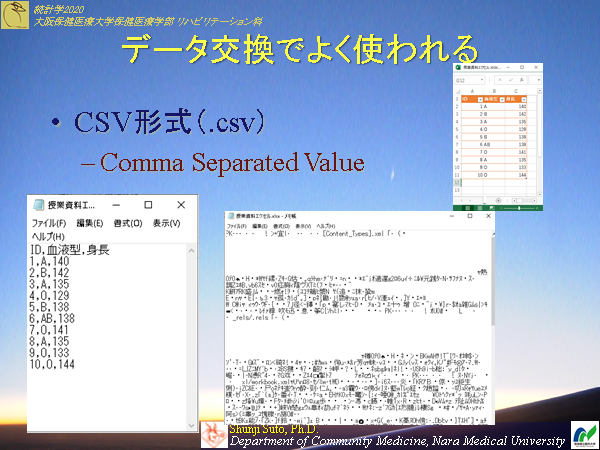
csv形式のファイルは以下
medbbstat2023-0101.csv

統計学（２）代表値と散布度

概要
集団の状況を示す統計量の代表値や散布度について

量的変量の統計量

度数は質的変量でも算出可能だが，今回の話は量的変量のみの話
ただし，量的変量は質的変量の性質も持っているので，その性質を利用している統計量もあります．

代表値

average（その集団でとりまとめたデータを数値一つで表す。excelはaverage関数で算術平均を出すが、代表値の代表ということだからと解釈しています）

平均

算術平均

mean（算術平均以外にも相乗平均などもあります）
1/n・Σx_i
パレートの法則（80-20の法則）
代表値なのに実在しない場合がある　→　集団の指標（重心）であって、事象を代表する値そのものを示しているとは限らない

幾何平均（相乗平均）

全て掛け合わせて累乗根をとる

加重平均

重みづけ平均
例えば　ミニテストと期末試験の平均をとる　→　そのままの平均で良いの？
度数分布表を用いた平均もこの方法・・・Σ（階級値×階級の度数）／ｎ

例題２－１）

あるクラスの生徒の身長を計測したところ以下のような結果が得られた

a)この集団の算術平均を求めよ
b)先週作成した同データの度数分布表から集団の平均値を求めよ
c)もしできるならこの集団の幾何平均を求めよ

中央値

median（別名第２四分位数）
量的変量を順序尺度で処理した代表値
順番に並べたとき真ん中の順位にきた個体の値
個体数が偶数の時は真ん中2つの数値の平均値

最頻値

mode（流行，はやり）
違う意味で数の理論（多数決）の世界
量的変量を名義尺度で処理した代表値
名義尺度でわかることは一緒か違うか
階級毎に度数をカウント
一番多いところの階級値
一位が同点の時は併記

平均値と中央値の考え方の違い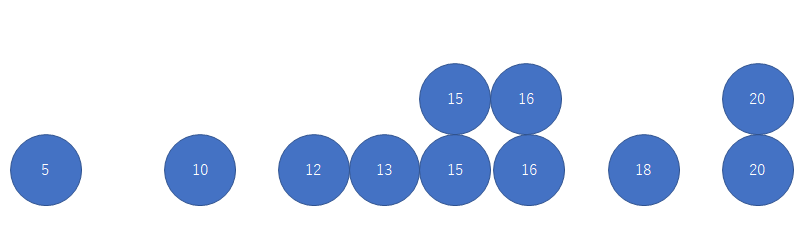 平均値（14.55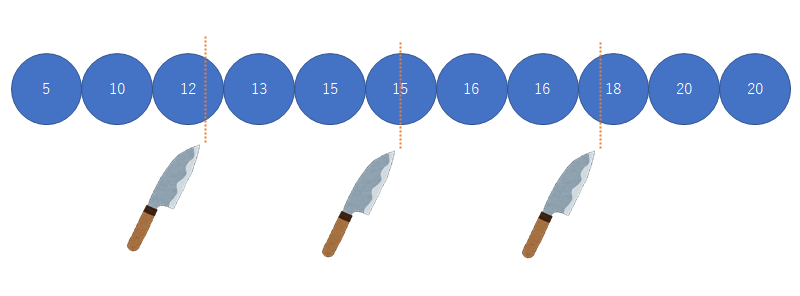） こちらは分布なんて関係なく中央値（15） データの分布に依存する（パラメトリック）＝平均値　と　データの分布に依存しない（ノンパラメトリック）＝中央値，最頻値の関係がわかるかなと思います 例えば５が０に変わってしまうと平均値は大きく変わりますが，中央値は変わりません パラメトリック・・・数値に依存する（数値の分布によって値が影響を受ける）というとイメージしやすいのかな？

例題２－２）

あるクラスの生徒の身長について
a)この集団の中央値を求めよ
b)この集団の最頻値を先週作成した度数分布表から求めよ

散布度

dispersion

範囲

ある値～ある値までの広さ

範囲

Range
R=最大値－最小値

特徴
　外れ値もひらう
　算出が用意

最大値と最小値がわかればその集団のバラツキがわかる
最大値maximum excel max関数
最小値minimum excel min関数

四分位範囲

小さい順（昇順）に並べて集団を4分割
分割する所の値を小さい方から第１四分位数（Q1），第２四分位数（Q2）＝中央値，第３四分位数（Q3） 四分位範囲IQR(interquartile range)=Q3-Q1

四分位数の話

四分位数は出し方が何種類かあります．近年は高校で教育されていますがその方法も従来のものと異なるので細かい計算をするのはやめておきます

パーセンタイルの話

第１四分位数は２５％タイル値，第２四分位数は50%タイル値，第３四分位数は75%タイル値のことです．
混乱しがちなのは第一四分位数が小さい方から数えてなのに，大きい方から数える人がいます
その時はパーセンタイルで整理したほうが良いかもしれません（100%＝最大値）というのは納得できると思うので上から75%＝第3四分位数

箱ひげ図

四分位範囲をグラフ化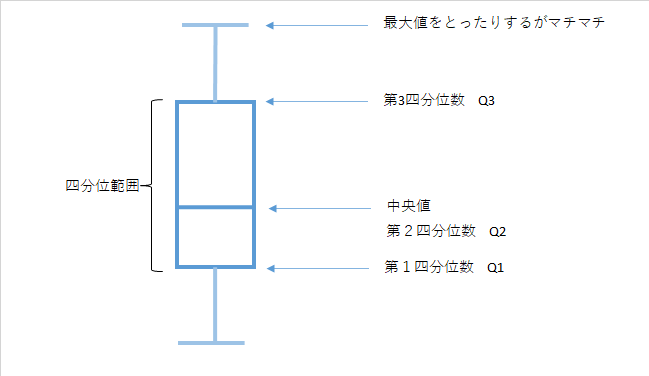

偏差

Deviation
ある基準とする値からのズレ
それぞれのズレの平均を求めたら良いのだろう・・・

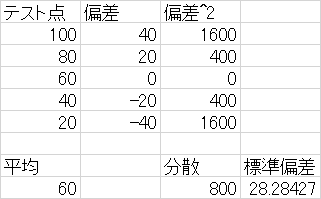
分散

variance
excel関数はVAR
偏差を平方（二乗）したものの平均
ここでは記号をσ^2とする． Σ(Xi-Xbar)^2／n
何故平方するの？
どうしても偏差の平均を求めることが出来ないので

標準偏差

Standard Deviation
記号はσ
σ=√(σ^2)

例題２－３）

あるクラスの生徒の身長について
a)この集団の分散を求めよ
b)この集団の標準偏差を求めよ

平均値から±標準偏差と書くとその集団がどのような分布なのか（何となく示せますよね）

はてなブログに投稿しました
EXCELで発生する誤差および回避する方法について（有効桁数大切という話だけど私もexcelも一緒と判定したのに） - Medbb's blog https://t.co/z5vcKQNTRv#はてなブログ

— めどぶぶ (@medbb) January 3, 2024

統計学（３）母平均と母分散の点推定

概要
その集団の状況を示すのではなく，その集団を含む集団全体を推定することについて

記号について

推定の話になると記号の取り扱いで混乱するのでここで整理しておきます．
分かりやすさを優先して整理したので，皆さんの使っている教科書などの表記は＜参考＞の論文を確認し読み替えください
μ・・・集団全体（母集団）の算術平均＝母平均
σ^2・・・集団全体（母集団）の分散＝母分散
σ・・・集団全体（母集団）の標準偏差＝母標準偏差

xbar・・・集団の一部（標本）の算術平均＝標本平均＝母平均の不偏推定量
s^2・・・集団の一部（標本）より求めた母集団の分散の推定量=不偏分散（母分散の不偏推定量）
s・・・集団の一部（標本）より求めた不偏分散よりもとめた標準偏差＝母標準偏差の推定量

参考

統計学テキストの「分散」の表記に関する調査（札幌学院大学総合研究所紀要　巻 1, p. 1-10, 発行日 2014-03-31）
https://sgul.repo.nii.ac.jp/records/1807

母集団と標本

母集団

対象としている集団の全体のこと
無限母集団と有限母集団がある

標本

対象としている集団の一部
偏ってしまうことに注意
例）森で取れた昆虫の標本を作成する際、どうしても森全体の昆虫の分布から偏ってしまう

取り扱う標本について

母集団は20000人の収縮期血圧データ（整数）
その集団の一部を抽出

母平均の推定

得られた標本より求めた平均をそのまま母集団の推定値とする

例題３－１

以下の標本より平均値を求めよ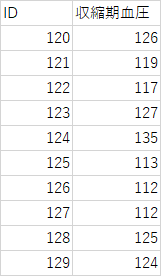

点推定

先程の例題で算出した値で母集団の特性値（母数）を推定すること
推定で求められるのは偏った推定にならないこと．
・標本が偏っていたら推定値は偏る
○標本が偏っていなくても計算方法によっては推定値が偏る

利点

計算が容易
平均値の場合，計算式が母集団全体の値を求める時と標本から推定する時と同じで良い

欠点

必ずしも推定値が実際と一致するわけではない・・・むしろ外れて当然
サンプルサイズ１０の時（母集団から２０００の標本が作成できる）のヒストグラム

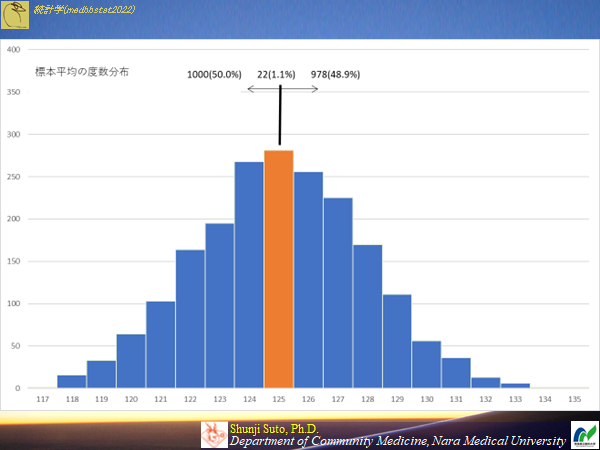
ピッタシ一致するのはサンプルサイズ10の時で1.1%（98.9%はハズレ）

推定の精度を上げるためには

標本数を大きくすればよい・・・測定を繰り返して行いその平均をとると精度は上がる
サンプルサイズを１００にした時の（母集団から２００の標本が作成できる）のヒストグラム

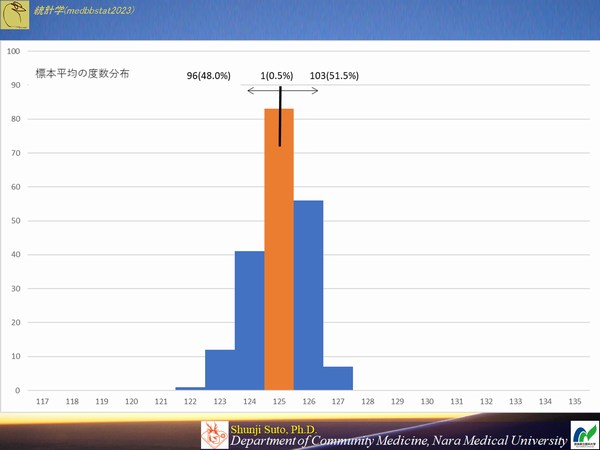
精度は上がるものの，ピッタシ一致する確率も上がるとは限らない

母分散の推定

例題３－２

以下の標本より標本の分散を求めよ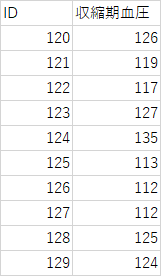

点推定

先程の例題で算出した値では母集団の特性値（母数）の推定はできない
推定で求められるのは偏った推定にならないこと．
・標本が偏っていたら推定値は偏る
×標本が偏っていなくても計算方法によっては推定値が偏る
標本の平均を用いサンプルサイズ１０の時（母集団から２０００の標本が作成できる）のヒストグラム

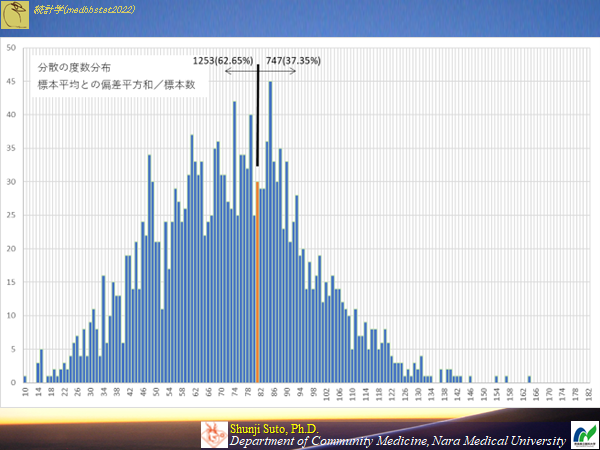
低めの値が多くなる傾向で偏っている．
母集団の平均（本来知る由もない）を用いサンプルサイズ１０の時（母集団から２０００の標本が作成できる）のヒストグラム

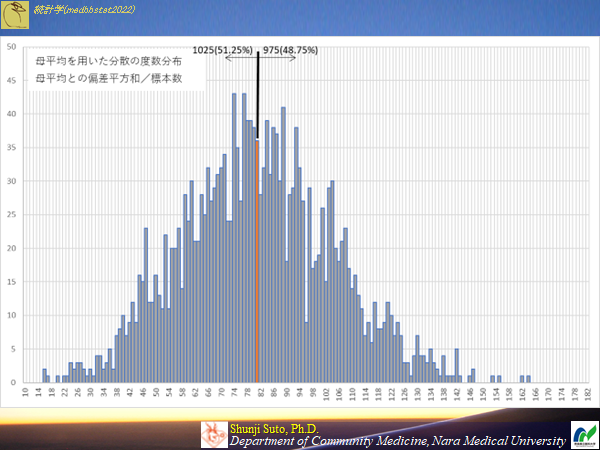
偏った推定にならないものの，本来知る由もない母平均を使えるわけがない（そもそも母数知っているなら推定は不要でしょう）

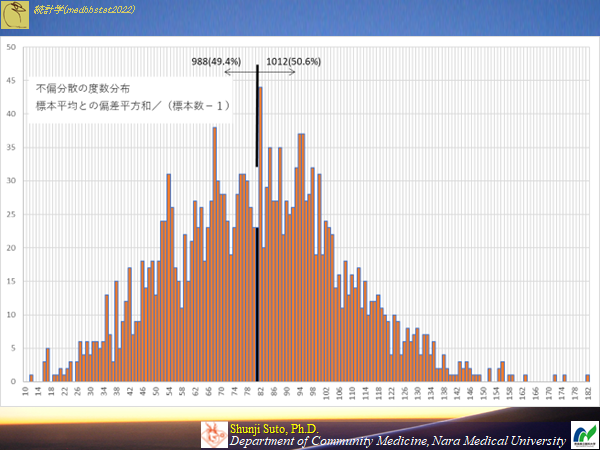
不偏分散

標本の平均を用いて母分散の推定を行う．
母平均と標本平均は（ほぼ）異なるので，母平均と標本平均の差も考慮して分散を求めたもの
（無論母平均は分からないが母平均と標本平均の差を考慮している）
s^2=Σ(Xi-Xbar)^2／(n-1)
nで除するよりn-1で除したほうが，値が大きくなるのは当然なので，低めの値が出るのなら少し分母を小さくした方が大きくなるのは理解できるが（ケーキを3人で分けるのか4人で分けるのか）なぜ１引くだけ？？となると思います

参考

不偏分散は何故nではなく（n-1）で除するのか（生物統計学2018奈良医大）
https://medbb.net/education/nmubiostat2018/index.html#VAR

例題３－３

以下の標本より母集団全体の分散および標準偏差を求めよ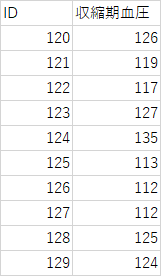

以降，追加分

中心極限定理

母集団の分布によらず（例えば母集団のデータがサイコロのように一様分布だったとしても），抽出した標本の平均値は標本数が大きくなるほど近似的に正規分布に従うという性質があります．

正規分布に従う事象は世の中で多くみられます．
ポイントとしては標本数が増えるほどヒストグラムが中心に集まっていっているというのも確認しておいてください
実験の際に何回も測定すると精度が上がる話を思い浮かべていただけたら納得いくかと思います

受講者の皆さんの疑問に対する回答

不偏分散の話はよく分かったけどn数が多い場合は普通に分散求めるケースがありますが良いの？

まず，対象とする集団が母集団そのものであれば記述統計の話なのでn数を用います．
対象とする集団が母集団そのものでなければ，標本ということになりますので母集団を推定したいというのであれば，記述統計の時と少し事情が異なります．n-1で計算する話（不偏分散）が基本になります．
ただし，サンプルサイズが大きければn-1≒n となりますので　実際に影響を与えない場合はありえます．
例えば扱っている数が多く，また取り扱っているデータの有効桁数など考慮した場合，違いが無いのであれば，実務の面では問題にならないからだと思います．
私なら結果が一緒でも不偏分散で求めたほうが説明の際に辻褄が合うのでそちらをお勧めします．事情があり通常の分散式を用いたほうが良いのであれば，上記のように実際に取り扱うデータの条件では分散も不偏分散もどちらも変わらないレベルであること，もしくは差異が出るのであればその点について示すと思います

そもそも分散ってなに？何を示しているの

偏差の平均を求めたいのですが，そのまま求めようとすると0しか出てきません・
負の値が邪魔をしているので，自乗することで回避した値（偏差平方）の平均は算出できるので，その平均をとったものになります．
無論単位を元に戻す（正の平方根をとる）と標準偏差となりますが，バラツキ具合（散布度）を示します
偏差を用いた散布度について分散の話を中心にしているのは，不偏分散は母分散の不偏推定量ですが，不偏分散より求めた標準偏差は不偏推定量とは言えないからです
なお，解釈としては分散も標準偏差も値が大きいほど個々の値のバラツキ具合は激しく，値が小さいほど平均値近辺に分布している集団であることを示します．
平均点が全て同じ60点としても
100,80,60,40,20　ならば　分散は800　標準偏差は28.3
80,70,60,50,40　ならば　分散は200　標準偏差は14.1
70,65,60,55,50　ならば　分散は100　標準偏差は7.1
とそれぞれの集団のバラツキ具合が小さいほど分散や標準偏差の値が小さくなることがわかるかと思います

なお，不偏分散から求めた標準偏差が不偏推定量にならない話はブログに掲載しました．
ご興味のある方はどうぞご覧ください

はてなブログに投稿しました
不偏分散の正の平方根は不偏標準偏差でよろしいのか（よろしくない） - Medbb's blog https://t.co/fHg4q2ji6e#はてなブログ

— めどぶぶ (@medbb) January 9, 2024

次回の予告

標本から求めた母集団の平均値の推定値と，標本から求めた母集団の標準偏差の推定値がわかると区間推定を行うことが出来ます．
点推定だと母平均をピッタリ当てることはほぼほぼ無理でしたが区間推定だと，その気になれば１００％当てることが出来ます．

統計学（４）母平均の区間推定

概要
点推定（算術平均）に散布度（標準誤差）を用いて区間推定を行うことについて

区間推定

点推定に幅をもたせたもの．
幅の定義は確率（どの程度あたるものか）
∴100%あたる推定に意味は無い→確実に当たる幅を設定したら達成できるので
一般的に95%の確率で当たる区間（95%の信頼区間）で幅を決めている

平均値の区間推定

母平均の点推定値を中心に散布度（標準偏差）をベースにして±の幅を持たせる．

問題点１

標準偏差をベースとは言うものの，サンプルサイズが大きくなると標本平均のバラツキは小さくなるという話があった・・・
標本平均のバラツキ具合はサンプルサイズが大きくなると小さくなるという話．
サンプルサイズ１０の時（母集団から２０００の標本が作成できる）の標本平均のヒストグラム

サンプルサイズ１００の時の（母集団から２００の標本が作成できる）の標本平均のヒストグラム

標準誤差

・標準偏差は標本の分布のバラツキ具合を示したもの
・標準誤差は母集団から抽出した標本の平均値のバラツキ具合
SE=σ／√n

例題４－１

サンプルサイズ10の時の平均値（標本数2000）の不偏分散を求めたところ8.02でした．
それより求めた標準偏差は2.83になります
それをサンプルサイズを100とした時，不偏分散，それより求めた標準偏差，はどの程度の値になるでしょうか？
（ちなみにサンプルサイズ100の時の平均値（標本数200）を実際に求めたところ，不偏分散は0.84標準偏差は0.92になりました）

問題点２

点推定±標準誤差で区間を定めると，区間を推定していることになるが100%の確率で当たらない　ということしかわからない．
何％の確率で当たるのだろう？

中心極限定理（再掲）

標本の大きさが十分であれば標本平均の分布は正規分布
　→実験の時に複数回測定してその平均をとりましょう・・・・測定の精度が上がると言われた記憶 　→測定回数を増やせば増やすほど
　→正しく何回も測定されたのであれば偶然誤差の発生は正規分布に従う

誤差の話は二つの要因

正規分布

左右対称の釣鐘状分布
平均値に近いほど出現率が高く遠ざかるに従って低くなる（ことが多い）
今更ながらだが，標本平均のヒストグラムって正規分布の形ですよね

標準正規分布

平均値が０標準偏差＝１（分散も１）になるように値を変換したもの
偏差値は平均値を50、標準偏差＝１０になるように値を変換したもの

標準正規分布表

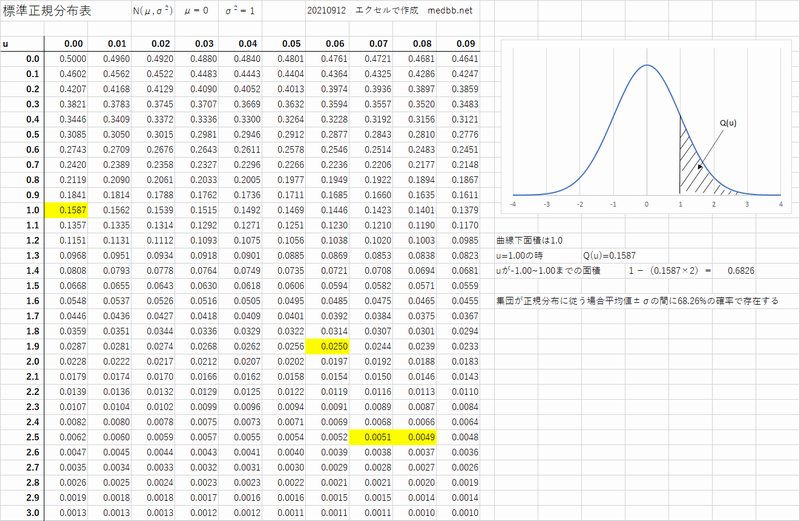
標準正規分布表のPDF版はコチラから

標準正規分布の世界は平均値が0標準偏差が1の世界→95%の確率で含まれる区間（信頼区間）は　0±(1×1.96)　になります．
分布表から調べなくても1.96は見つけることが出来ます　←　EXCEL[=NORM.S.INV(0.975)]
この関数は分布表と同じく上側の面積（=確率）を返してくれる変数ですので[=NORM.S.INV(1-0.025)]としたほうが解釈しやすいかなと思います．

例題４－２

ある試験の受験者１００人から点を教えてもらったところ平均値（点推定）＝６５点　標準偏差（点推定）＝１８点であった．
受験全員（＝母集団）の平均値の区間推定を信頼区間95%で示せ

回答例

というところで今回のお話はおしまい

記述統計を２回．推測統計の平均値の推定を2回．進め方としてはじっくり取り組めるよう進めたつもりです
これで推定は完璧なのか？と言われると・・・
平均値の話はなぜ母集団の分布に関係なく正規分布を用いるかですが，中心極限定理のお陰です
ところが正規分布にも欠点がありまして，サンプルサイズが小さいと95%信頼区間と言いながら実際95%（すなわち20回推定したら19回当たる）もあたりません
中心極限定理の動画を見直すと，n数が少ないときなんとなく形が整っていない感じでしたよね
とあるビール会社の技師さんがstudentというペンネームでこの問題を解決する確率分布を発表しました
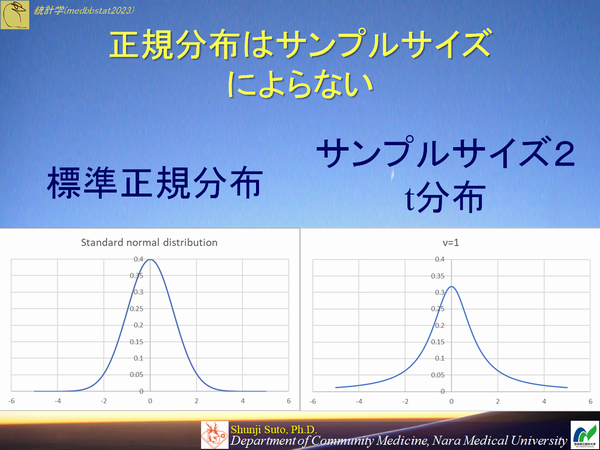
それがt分布です．
最後にt分布と標準正規分布の違いだけご覧いただき今回の講義は終わりとします

リアルで私の授業を受講している方は試験に向けて頭の中を整理しておいてください．実力を発揮されることを祈っております．
お付き合いいただいた一般の皆様，質問を頂きありがとうございました．お陰様で私自身考える機会を頂きました．
またなにかしらの機会でお会いできることを楽しみにしております．

参考

酒井 弘憲，ギネスビールと統計家ペンネーム　スチューデント，ファルマシア51巻12号,2015
https://www.jstage.jst.go.jp/article/faruawpsj/51/12/51_1168/_article/-char/ja