大阪保健医療大学 統計学2024(保健医療学部 リハビリテーション科)
2024年度開講にあたって
https://medbb.net/education/2024init/
困った時,オンラインでのサポートやなにかありましたら以下からご連絡ください
私へ連絡・オンラインオフィスアワー予約
演習についてはサーバー上に残しておいてください
授業メニュー
第01回 データの取得(1)
第02回 データの取得(2)
第03回 記述統計(Ⅰ)度数分布表
第04回 記述統計(Ⅱ)度数分布図
第05回 記述統計(Ⅲ)代表値
第06回 記述統計(Ⅳ)散布度
第07回 推定(Ⅰ)正規分布
第08回 推定(Ⅱ)中心極限定理
第09回 推定(Ⅲ)母数の推定(点推定)
第10回 推定(Ⅳ)母平均の区間推定
第11回 検定(Ⅰ)2群の差の検定(パラメトリック)
第12回 検定(Ⅱ)2群の差の検定(ノンパラメトリック)
第13回 検定(Ⅲ)カイ二乗検定
第14回 判断分析(Ⅰ)感度・特異度
第15回 判断分析(Ⅱ)ROC曲線
第01回 データの取得(1)
EXCELの利用
本授業ではMS-EXCELで 起動してみましょう.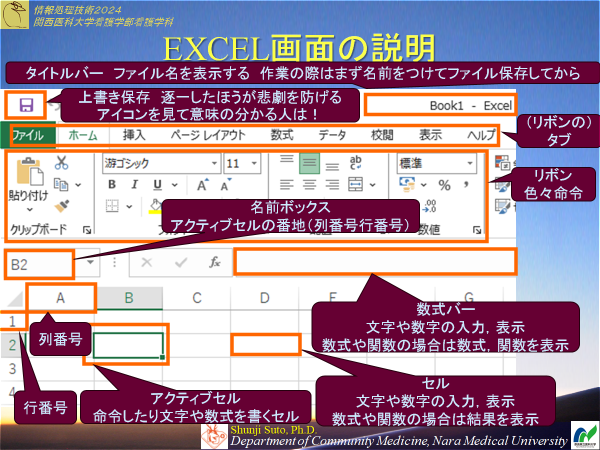
キーワード
セルセル番地
数式バーとセルの表示
計算式
関数
セルの参照(絶対,相対)
グラフの作成
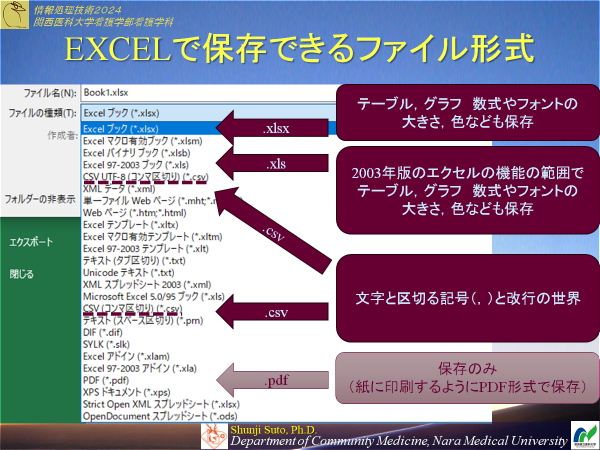
保存は大切
保存形式はありのままなら,標準形式(xlsx),データだけならcsvが便利
CSV形式
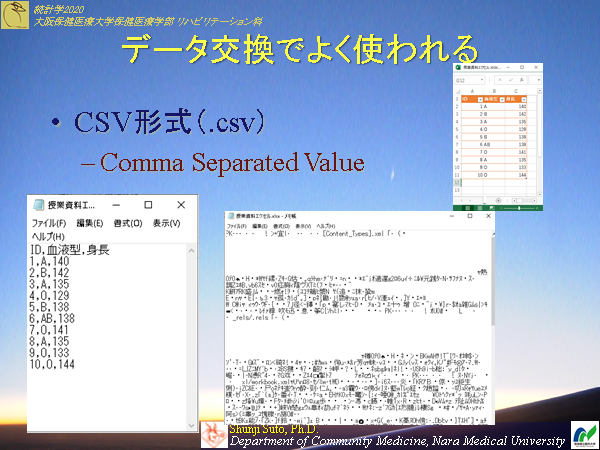
演習1-1
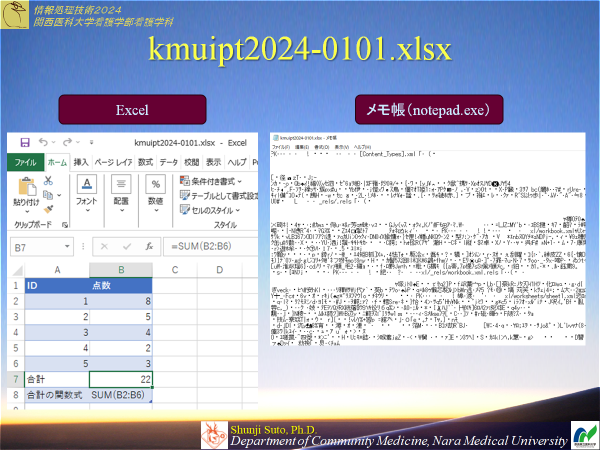
示すファイルを用いてアプリケーションや文字コードによってデータがどのように表示されるか確認せよxlsx形式(Excel標準)のファイル
csv形式(文字コードはwindows標準のShift-JIS形式)
csv形式(文字コードは世界中で使われるUTF-8形式)

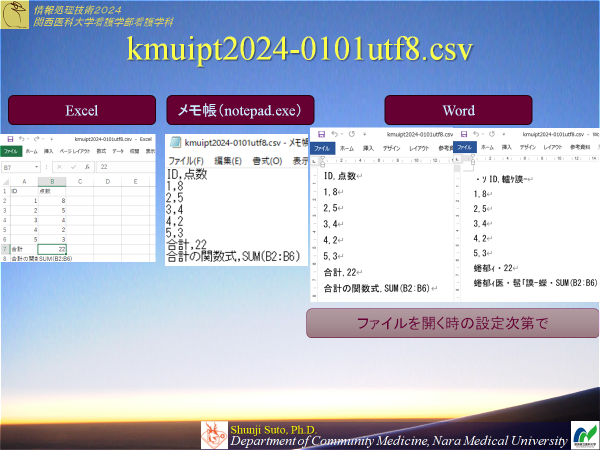
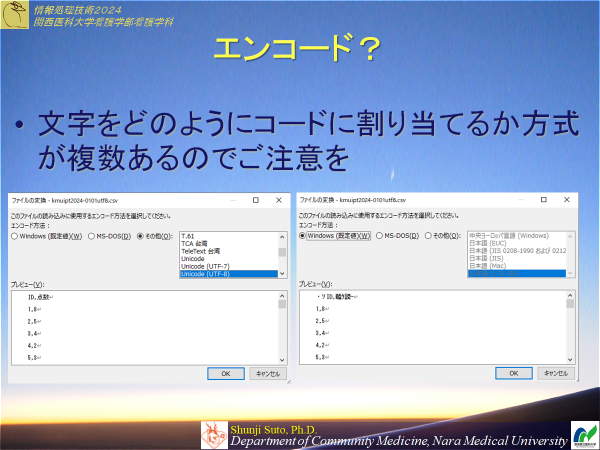
<参考>UTF-8:Tech Basics/Keyword(@IT ITmedia Inc.)
https://atmarkit.itmedia.co.jp/ait/articles/1603/28/news035.html
データ形式(Excel)
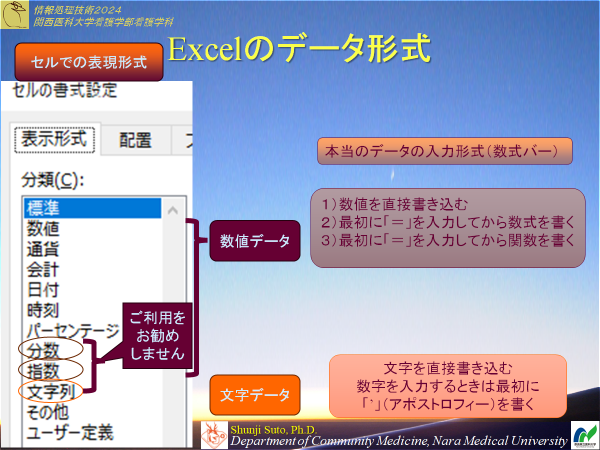
演習1-2
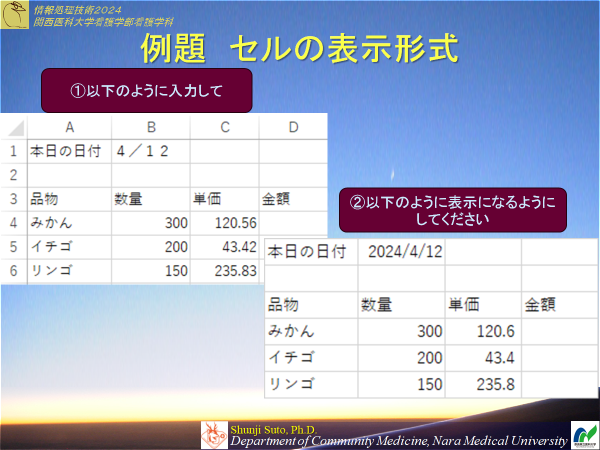
演算と関数
四則演算 +-×÷ → + - * /セルの参照
極力手打ちでデータを入力しないように.(人は間違える)エクセルに,どのセルの値なのか場所を教えてあげる
演習1-3
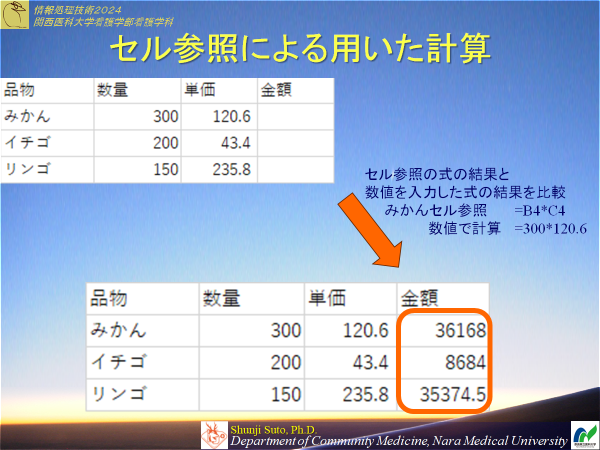
演習1-3の結果より合計金額と平均金額を算出する
よく使う計算は関数が用意されている.
合計はsum関数 平均はaverage関数
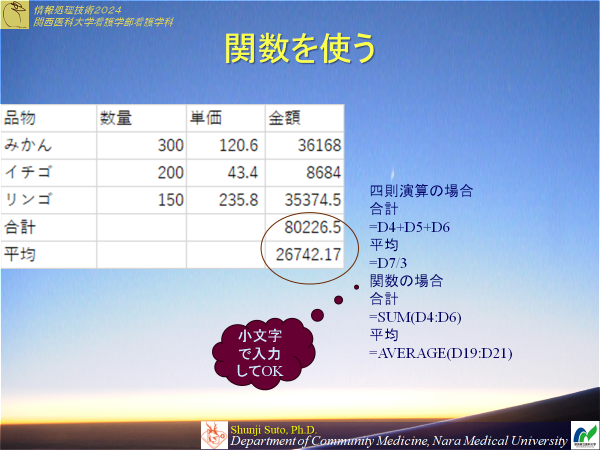
演習1-4
以下のファイルをダウンロードし空欄部分を計算してくださいkmuipt2024-0201.csv
以下リクエスト方式で内容がシラバスよりある程度逸脱します
不偏分散の話
stdev.pとsの話1回目2回目ここまで
母平均の推定
得られた標本より求めた平均をそのまま母集団の推定値とする点推定
・標本が偏っていたら推定値は偏る○標本が偏っていなくても計算方法によっては推定値が偏る
利点
計算が容易平均値の場合,計算式が母集団全体の値を求める時と標本から推定する時と同じで良い
欠点
必ずしも推定値が実際と一致するわけではない・・・むしろ外れて当然サンプルサイズ10の時(母集団から2000の標本が作成できる)のヒストグラム
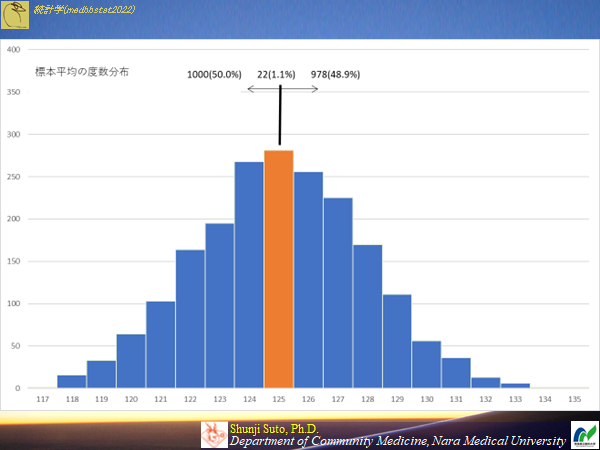
ピッタシ一致するのはサンプルサイズ10の時で1.1%(98.9%はハズレ)
推定の精度を上げるためには

標本数を大きくすればよい・・・測定を繰り返して行いその平均をとると精度は上がる
サンプルサイズを100にした時の(母集団から200の標本が作成できる)のヒストグラム

精度は上がるものの,ピッタシ一致する確率も上がるとは限らない
母分散の推定
点推定
先程の例題で算出した値では母集団の特性値(母数)の推定はできない推定で求められるのは偏った推定にならないこと.
・標本が偏っていたら推定値は偏る
×標本が偏っていなくても計算方法によっては推定値が偏る
標本の平均を用いサンプルサイズ10の時(母集団から2000の標本が作成できる)のヒストグラム
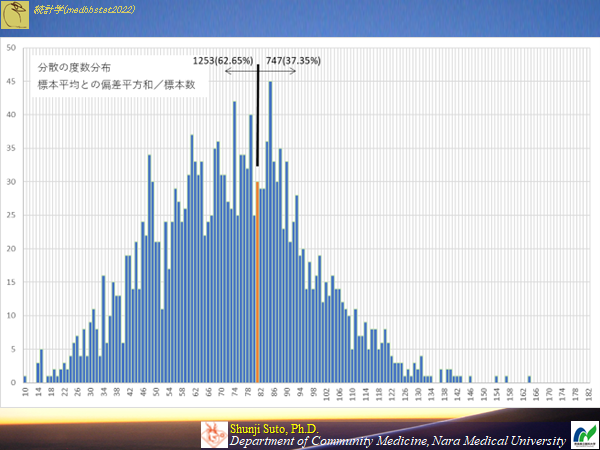
低めの値が多くなる傾向で偏っている.
母集団の平均(本来知る由もない)を用いサンプルサイズ10の時(母集団から2000の標本が作成できる)のヒストグラム
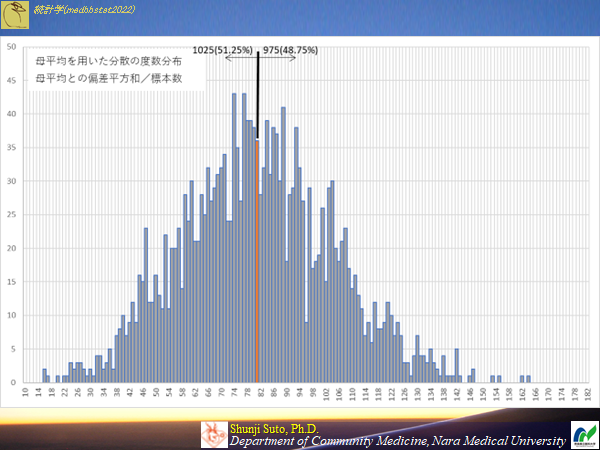
偏った推定にならないものの,本来知る由もない母平均を使えるわけがない(そもそも母数知っているなら推定は不要でしょう)
不偏分散
標本の平均を用いて母分散の推定を行う.母平均と標本平均は(ほぼ)異なるので,母平均と標本平均の差も考慮して分散を求めたもの
(無論母平均は分からないが母平均と標本平均の差を考慮している)
s^2=Σ(Xi-Xbar)^2/(n-1)
nで除するよりn-1で除したほうが,値が大きくなるのは当然なので,低めの値が出るのなら少し分母を小さくした方が大きくなるのは理解できるが(ケーキを3人で分けるのか4人で分けるのか)なぜ1引くだけ??となると思います
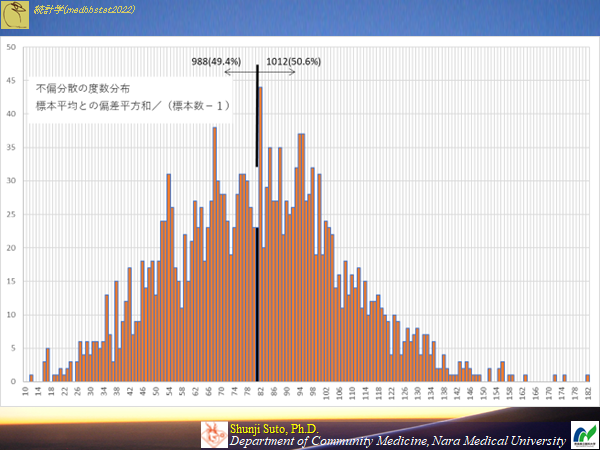
参考
不偏分散は何故nではなく(n-1)で除するのか(生物統計学2018奈良医大)
https://medbb.net/education/nmubiostat2018/index.html#VAR
標本の平均を用いると偏差平方和(分散)は最少となる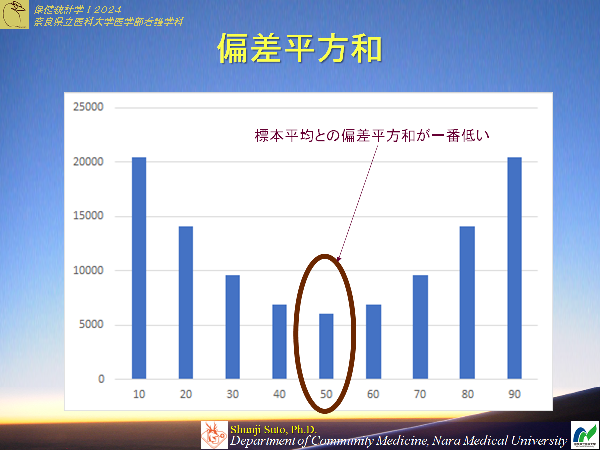
第02回 データの取得(2)
統計でみる市区町村のすがた
https://www.stat.go.jp/data/s-sugata/index.htmlを用いてデータを用いる際の注意点など理解しながら進めましょう
演習2-1 人口・世帯のデータより47都道府県のデータのみ抽出したテーブルを作成せよ
演習2-2 人口・世帯のデータより奈良県の市町村のみ抽出したテーブルを作成せよ
3回目4回目ここまで
演習2-3 人口・世帯のデータより奈良県の保健医療圏別でテーブルを作成せよ
<参考>
二次医療圏(e-govポータル)
https://data.e-gov.go.jp/data/dataset/mhlw_20150115_0041
5コマ目ここまで
第03回 記述統計(Ⅰ)度数分布表
データ
観測値や測定値のこと(数値)だけでなく性別など文字の場合もある.コンピュータ処理するとき,文字だと扱いにくい時があるのでその時は数字に置き換える(→コード変換)
例えば都道府県名であれば 北海道→01 青森県→02 奈良県→29
全国地方公共団体コードの上二桁=都道府県番号
|
<参考>全国地方公共団体コード(総務省) https://www.soumu.go.jp/denshijiti/code.html |
変量(データ)の分類
変量は様々なものがあるがそれらの性質をとりまとめ分類することが出来る。それぞれを尺度と呼び、4つに分類するのが一般的である
1分類尺度(名義尺度)
2順序尺度
3間隔尺度
4比尺度(比例)(比率)
1,2を質的変量(定性的)
3,4を量的変量(定量的)
性質としては上位互換性があり
4>3>2>1
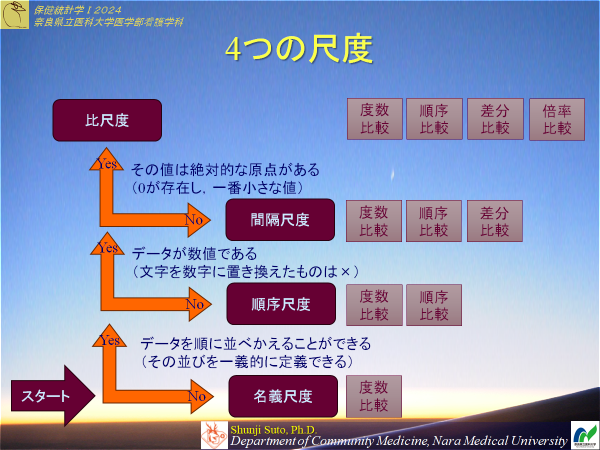
統計量
取りまとめたものを「量で」示したもの.質的変数であっても度数(個数,人数など数えるもの)については「量」として示すことが出来る度数
どのようなデータでも度数を示すことは可能度数分布表
この授業では量的変量の度数分布表を作成する場合 A~B は A以上B未満として取り扱うそれぞれのデータ(変量)の数(出現頻度)をまとめたもの
変量が名義尺度の時は多い順(お作法として。但しその他を出すなら一番最後)
順序尺度以降であれば順(名義尺度でも比較のためにお作法を破ることはある)
度数 ・・・出現頻度
相対度数・・・総出現頻度を1(100%)としたときのそのぞれの度数のしめる割合
累積度数・・・上位の変量の度数もあわせた度数
累積相対度数・・・累積度数の相対版
演習3-1
以下の店名別のみかんの売り上げデータより度数分布表を作成せよ| 日付 | 店名 | 数量(箱) |
|---|---|---|
| 9月1日 | 奈良本店 | 1400 |
| 9月1日 | 大和郡山店 | 700 |
| 9月1日 | 大和高田店 | 450 |
| 9月2日 | 奈良本店 | 1000 |
| 9月2日 | 大和郡山店 | 900 |
| 9月2日 | 大和高田店 | 1100 |
| 9月3日 | 奈良本店 | 1600 |
| 9月3日 | 大和郡山店 | 400 |
| 9月3日 | 大和高田店 | 850 |
| 店名 | 度数 | 相対度数 | 累積度数 | 累積相対度数 |
|---|---|---|---|---|
| 1.00 | ||||
| 計 | 1.00 | ----- | ----- |
演習3-2
kmuipt2024-0501sjis.csv セリーグパリーグ関係なく優勝チームの度数分布表および,優勝監督の度数分布表を作成せよ演習3-3
優勝監督の度数分布表を作成せよ.さらにセリーグとパリーグの内訳も表記の事量的変数の度数分布表
量的変数の場合はその数値だけで度数を積み上げようにもなかなか上手くいかない場合がある.血圧 163.5mmHg 164.2mmHg 162.5mmHg・・・どれも度数を積み上げられない → 区間を設定する
|
「A~B」は「A以上B未満」と読む格好と思っていたが,分野などによって違うようです 「A以上B以下」のようにどちらの階級にも属してしまう可能性のある設定はしないように. |
| 階級 | 階級値 | 度数 | 相対度数 | 累積度数 | 累積相対度数 |
|---|---|---|---|---|---|
| 130~140 | 135 | ||||
| 140~150 | 145 | ||||
| 150~160 | 155 | ||||
| 160~170 | 165 | ||||
| 170~180 | 175 | ||||
| 計 | ----- | ----- |
演習3-3
以下のデータ(身長)をダウンロードし10歳階級別,5歳階級別の度数分布表を完成させよ また身長の区間推定を正規分布およびt分布で行い比較せよ medbbstat2023-0101.csv8-9回 母平均の区間推定
概要点推定(算術平均)に散布度(標準誤差)を用いて区間推定を行うことについて
区間推定
点推定に幅をもたせたもの.幅の定義は確率(どの程度あたるものか)
∴100%あたる推定に意味は無い→確実に当たる幅を設定したら達成できるので
一般的に95%の確率で当たる区間(95%の信頼区間)で幅を決めている
平均値の区間推定
母平均の点推定値を中心に散布度(標準偏差)をベースにして±の幅を持たせる.問題点1
標準偏差をベースとは言うものの,サンプルサイズが大きくなると標本平均のバラツキは小さくなるという話があった・・・標本平均のバラツキ具合はサンプルサイズが大きくなると小さくなるという話.
サンプルサイズ10の時(母集団から2000の標本が作成できる)の標本平均のヒストグラム

サンプルサイズ100の時の(母集団から200の標本が作成できる)の標本平均のヒストグラム
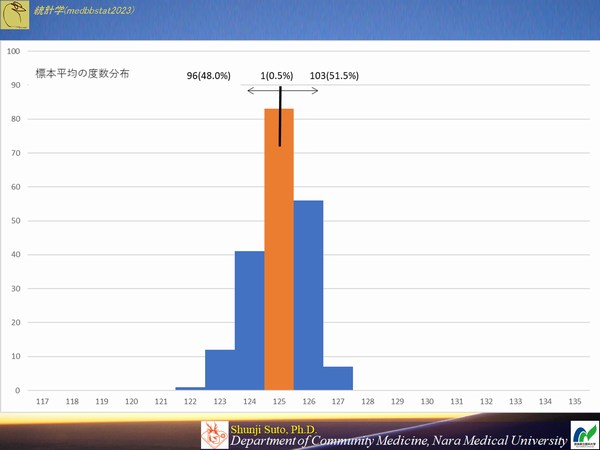
標準誤差
・標準偏差は標本の分布のバラツキ具合を示したもの・標準誤差は母集団から抽出した標本の平均値のバラツキ具合
SE=σ/√n
例題1
サンプルサイズ10の時の平均値(標本数2000)の不偏分散を求めたところ8.02でした.それより求めた標準偏差は2.83になります
それをサンプルサイズを100とした時,不偏分散,それより求めた標準偏差,はどの程度の値になるでしょうか?
(ちなみにサンプルサイズ100の時の平均値(標本数200)を実際に求めたところ,不偏分散は0.84標準偏差は0.92になりました)
問題点2
点推定±標準誤差で区間を定めると,区間を推定していることになるが100%の確率で当たらない ということしかわからない.何%の確率で当たるのだろう?
中心極限定理(再掲)
標本の大きさが十分であれば標本平均の分布は正規分布→実験の時に複数回測定してその平均をとりましょう・・・・測定の精度が上がると言われた記憶 →測定回数を増やせば増やすほど
→正しく何回も測定されたのであれば偶然誤差の発生は正規分布に従う
誤差の話は二つの要因

正規分布
左右対称の釣鐘状分布平均値に近いほど出現率が高く遠ざかるに従って低くなる(ことが多い)
今更ながらだが,標本平均のヒストグラムって正規分布の形ですよね
標準正規分布
平均値が0標準偏差=1(分散も1)になるように値を変換したもの偏差値は平均値を50、標準偏差=10になるように値を変換したもの
標準正規分布表
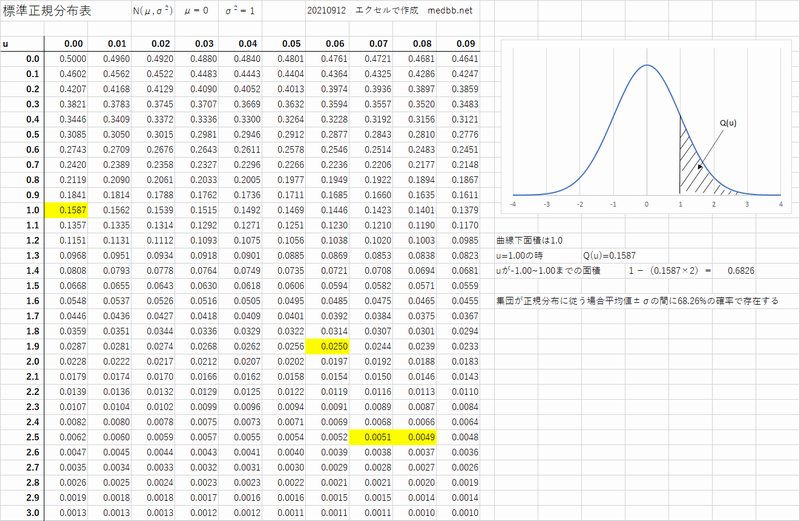
標準正規分布表のPDF版はコチラから
標準正規分布の世界は平均値が0標準偏差が1の世界→95%の確率で含まれる区間(信頼区間)は 0±(1×1.96) になります.
分布表から調べなくても1.96は見つけることが出来ます ← EXCEL[=NORM.S.INV(0.975)]
この関数は分布表と同じく上側の面積(=確率)を返してくれる変数ですので[=NORM.S.INV(1-0.025)]としたほうが解釈しやすいかなと思います.
例題2
ある試験の受験者100人から点を教えてもらったところ平均値(点推定)=65点 標準偏差(点推定)=18点であった.受験全員(=母集団)の平均値の区間推定を信頼区間95%で示せ
回答例

正規分布とt分布
検証データ ocrstat2021-0401.csv7,8回 ここまで(正規分布での判定まで)
t分布
母集団の平均値を推定するにおいて,標準正規分布を使うと上手くいかないケースがある・・・特に標本数が少ないと困っていたゴセットさんが標本数によって平均値の出現する確率が変化する分布を示しました.
諸々の理由でt分布と呼ばれています.
|
酒井 弘憲,ギネスビールと統計家ペンネーム スチューデント,ファルマシア51巻12号,2015 https://www.jstage.jst.go.jp/article/faruawpsj/51/12/51_1168/_article/-char/ja |
母集団の分散(標準偏差)が既知の場合(実際にはなかなかお見掛けすることは無いが),もしくはサンプルサイズが非常に大きく標本から求めたものの母集団の分散として取り扱って差し支えないものであれば正規分布で推定しても良い
t分布は標本より求めた母標準偏差の推定値(不偏分散に基づく標準偏差)を用いるが,標本の自由度(標本数より求める)によって変化する.
故に標本数が多くなるとt分布は正規分布に近似されていく.
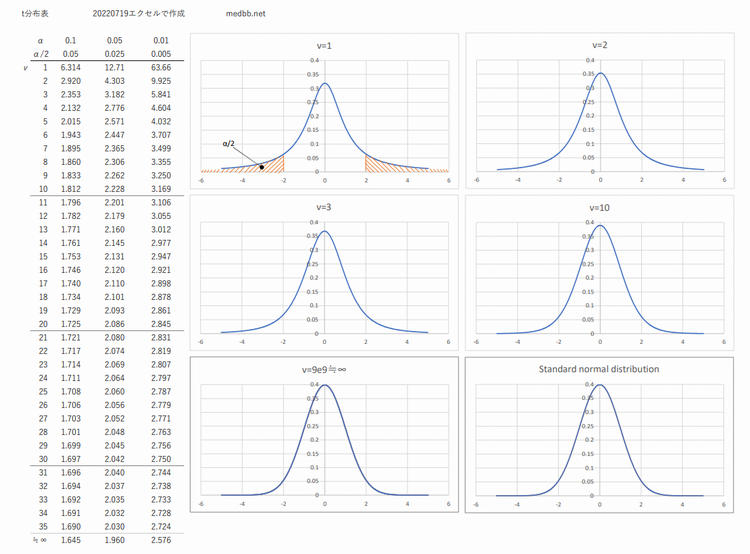
t分布のPDF版はコチラから
「自由度」νが出てきますが,以下考え方
標本の中で自由に振る舞うことが許されている値の数例えば標本から平均を求めたとき,その平均が母数の推定値としたら、自由に振る舞えない値が出てくる(つじつま合わせ)
t分布は抽出した標本数を基にしたものなので,正規分布のように一義的なものでは無く,標本数(自由度)によって確率分布が変わる
問 T.INV.2T()を用いて検証データの空欄部を埋めよ
第9,10回 検定(Ⅰ)2群の差の検定(パラメトリック)
科学的な話
科学が,それ以外の文化と区別される基本的な条件としては,実証性,再現性,客観性などが考えられる
実証性とは,考えられた仮説が観察,実験などによって検討することができるという条件再現性とは,仮説を観察,実験などを通して実証するとき,人や時間や場所を変えて複数回行っても同一の実験条件下では,同一の結果が得られるという条件
客観性とは,実証性や再現性という条件を満足することにより,多くの人々によって承認され,公認されるという条件
実証性
「考えられた仮説」が無いことには始まらない→仮説検証型それでは「考えられていない仮説」とは?
→まだ十分に確固たる仮説として成立していない仮説
仮説検証型と仮説探索型
仮説探索型とは「考えられた仮説」が存在せず(関心ある事象など),得られた結果は「考えられた仮説」になる可能性を有するので「まだ考えられたと言い切れない仮説」再現性
仮説を実証するために得られたデータから複数回,同一の検証結果になること「常に」同一の検証結果になることを求めていないが,それは求められないから
再現性の限界
再現性の条件は「仮説の実証を複数回行っても同一の結果が得られる」ことですが,その回数が無限であるならばその条件は永遠に満たされません.故に有限となりますが,それはある回数(x回)まで同一の結果としても,x+1回目以降同一の結果にならない可能性を含んだものになります.
これは未来において,その仮説が覆される可能性があることを示すもので,反証可能性といわれるものです.
再現性の限界を超える方法
「仮説の実証を∞回行っても同一の結果が得られる」実証で得られたデータについてどのようなものであっても同一な結果が出るように判定基準を定める
例題1 再現性の限界を超える(つまり同一の結果が100%出るような判定基準を定める)ことがよろしくない理由を考えよ
判定基準
「同一の結果」が100%の確率で出現しないことを示しておく必要が出てきます 例えば仮説の実証を行うにあたって検証データに対する判定基準を目標値(目標とする効果量)として設定した場合,達成してもその判定基準が「『同一の結果』が100%の確率で出現しない」ものか分かりません.例えばその目標値が医学的に妥当なものであったとしても,ここでは関係ない話になります
そうなると,確率に基づく基準で判定しないことには,再現性を満たすことが出来ません
故に仮説検定では効果量などで判定せずに確率に基づいて行います
同一の結果が帰無仮説になりますが,従来と異なることが起こったことによって同一の結果が得られなかったという形で証明をしています(背理法)
統計的有意差と臨床的有意差
得られたデータに基づき計算した確率が判定基準を下回った時に統計的有意差があると言います.知見は社会実装することで人類に貢献できますが,医療現場においては臨床的に意味があるとされる量を基準とする臨床的有意差が結果として求められます
無論社会で役立てていく知見としては,統計的有意差よりも臨床的有意差が重要になりますが,「科学的」な観点からは前者が支配的になります.
確率の違いを量で示すとき,その量はサンプルサイズにより変化します.故に臨床的有意差に基づきサンプルサイズを決定することで二つの違いを解消できます
例えば臨床的有意差が統計的有意差よりも大きい場合は再現性については確認できたものの臨床的な観点から確認はできません.統計科学的に良いが,医科学的には?という結果になります
一般にはサンプルサイズが大きいほど,精度の高い結果が得られるので良いという感覚に思いますが,それは区間推定の話で仮説検定において効果量の差を検証する場合は少し状況が異なります
統計的有意性とp値に関するASA声明
<参考>統計的有意性とP値に関するASA声明(日本計量生物学会)http://biometrics.gr.jp/news/all/ASA.pdf
以下の内容が指摘されています
1. p値はデータと特定の統計モデルが矛盾する程度をしめす指標のひとつ
2. p値は、調べている仮説が正しい確率を測るものではない
3. 科学的な結論は、p値がある値を超えたかどうかにのみ基づくべきではない
4. 適正な推測のためには、すべてを報告する透明性が必要
5. p値は、効果の大きさや結果の重要性を意味しない
6. p値は、それだけでは仮説に関するエビデンスのよい指標とはならない
仮説
仮説検定では確率に基づく判断基準を有意水準として確率で示します.以降は「新たな知見」に対する話で仮説検定を用いるケースが重要なので有意差検定を前提として話を勧めます
事象としては「同一の結果が得られる」「同一の結果が得られない」の二つにいずれかになります.
同一の結果が得られる仮説を帰無仮説(これまでと違いが無い仮説)H0,同一の結果が得られない仮説を対立仮説(これまでと違いがある仮説)H1と示します.有意水準は対立仮説H1の確率を示します
有意水準は通例5%とされることが多く,両側検定(効果量に違いがあるのか無いか)と片側検定(違いがが正の方向のものなのか,負の方向のものなのか)の二種類があります
差がある仮説の判定(有意差検定)
研究活動は「新たな知見」を見出すことを目的にしてますので,通常この検定になります.区間推定を思い描いていただいたら,概ね同様な話ですが表現の仕方が帰無仮説/対立仮説の二値化されることと,区間推定と違い帰無仮説に基づく話(例えば差が0としているならばその値が中心,区間推定の場合は標本から求めた平均が中心)になる違いがある程度です.
帰無仮説そのものは「考えられた仮説」ではないので採択された場合の判定は保留になります
帰無仮説が棄却された場合残された仮説は対立仮説のみとなります.こちらは「考えられた仮説」になります
背理法の考え方に基づく論理になりますが,もともと証明したい仮説(差がある)を偽であるとして,矛盾を導く出すことで判定する方法になります
現在はコンピュータにより確率を直接求めることは可能ですし,まどろっこしい流れに映りますが,違い(差)を直接判断しているのではなく「同一の結果が得られる」確率に基づき判定基準を定めているところが科学として重要であるから故と捉えています.
ですので確率そのものは,判定のためのものであって求めた値(統計量や確率)そのものに重きを置く必要はありません.効果量そのものに重きをおく方が知見の社会実装の観点から重要になります
仮説検定(有意差検定 両側検定)のフォーマット例
手順1 帰無仮説,対立仮説をたてる
帰無仮説H0:μ=150 対立仮説H1:μ≠150手順2 母集団が従うと見做す確率分布を定め,有意水準を決める
(例えば)正規分布に従うと見做し,有意水準両側5%とする手順3 今回取得したデータをもとに,母集団が従うと見做す確率分布における統計量を求める
(以下はケースX)ここではよろしくないの承知で,正規分布としました
取得したデータの平均値(標本の平均)と帰無仮説に基づく母集団の平均値(母平均)の差を,確率分布(標準正規分布)における差に変換する
帰無仮説H0がある集団の収縮期血圧μ=150mmhgとしたときに,得られたデータ(サンプルサイズn=36 標本平均xbar=147.3 不偏分散s^2=81)で検定を行う
考え方は区間推定と同じように現実の世界と確率分布の世界を行き来できるようにすること

基本的な考え方を正規分布で整理しましょう.
検定統計量は現実の世界における標本平均と帰無仮説で定めた値の差分xbar-μ,これが標準正規分布の世界でどのような統計量(z)になるのか
1)標準正規分布の世界はμ=0 現実社会でのμ=150 標本平均のμからのズレは147.3-150=-2.7となる
2)-2.7は現実社会(サンプルサイズn=36 標本平均xbar=147.3 不偏分散s^2=81)によるものなのでσ(ここでサンプルは標本平均を求めているので標本平均の標準偏差,すなわち標準誤差SE=√81/√36=1.5の世界 これを 標準正規分布の世界(σ=1)に合わせると -2.7/1.5=-1.8
手順4
検定統計量を用いて有意水準との比較,今回の標本が棄却域にあるのか否か(受容域なのか)判定する.1)(ケースX) |z|=1.8 p=0.0359×2(両側検定なので2倍)>0.05
帰無仮説を棄却できないので判定を保留する
2)(ケース1)有意水準よりも小さい場合 |z|=2.96 p=0.015×2(両側検定なので2倍)<0.05
帰無仮説を棄却し対立仮説を採択する 有意差がある
3)(ケース2)有意水準よりも大きい場合 |z|=1.45 p=0.0735×2(両側検定なので2倍)>0.05
帰無仮説を棄却できないので判定を保留する
注)標準正規分布表の場合確率まで求めることが可能だが,t分布表は統計量から確率を求めることはできないので統計量で比較する
例題2 有意差検定において背理法を使わなければならない理由を考えよ(何故,違いがあるという仮説を直接証明しないのか?)
1標本(1群)t検定
世の中(母集団)の基準値など,既に明らかになっている事柄と比較することで世の中の一般的な状況と対象とする集団が異なっていることを明らかにすることを目的例題3
物騒な話ですが,ある自動販売機に偽造通貨が使われているのではないかという話が私のところに舞い込んできた.話を聞くともっともらしい仮説が既にあるので検証することにした.
そこで,自販機に入っていた硬貨10円玉10枚を用いてこの仮説について仮説検定を行う
10円玉の硬貨μ=4.50gと比較して異なることが期待される検定
ここでは,とりあえず標準正規分布で検定してみましょう(よくないけど)
| 10円玉ID | 重量(g) |
|---|---|
| 1 | 4.55 |
| 2 | 4.53 |
| 3 | 4.23 |
| 4 | 4.50 |
| 5 | 4.51 |
| 6 | 4.31 |
| 7 | 4.38 |
| 8 | 4.54 |
| 9 | 4.35 |
| 10 | 4.30 |
確率を求める時は表もしくは
=NORM.S.DIST() を使いこなして
例題4
例題3の結果を先方にお伝えしたところ,適切な統計手法を用いていないとご指摘を受けました.そこで改めてt分布を用いて検定を行ってください =T.DIST.2T() を使いこなして
検定で注意する点
両側検定と片側検定の注意点
一緒な有意水準で比較した場合 片側は棄却域が存在しないことと,他方は棄却域が大きくなってしまう → 帰無仮説が棄却されやすくなる状況paired-t検定
例題4
新開発のシューズを2種類開発した.それぞれ同一被験者に従来型と新型を履いて5km走のタイムを計測し比較を行った.対応のある2群の差の検定を優位水準5%で行え
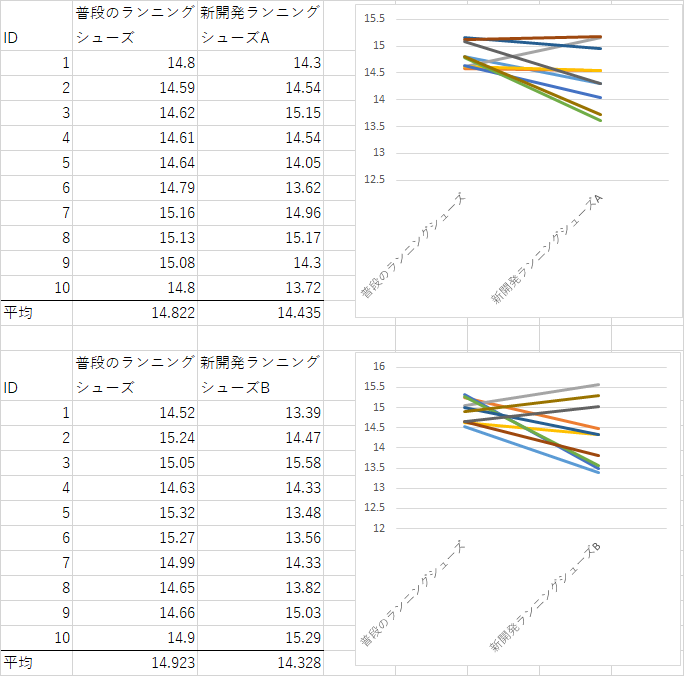
参考
令和元年度体力・運動能力調査結果の概要及び報告書について(スポーツ庁)
https://www.mext.go.jp/sports/b_menu/toukei/chousa04/tairyoku/kekka/k_detail/1421920_00001.htm
第13~14回 判断分析(Ⅰ)感度・特異度 判断分析(Ⅱ)ROC曲線
スクリーニング
無症状だがある疾患に罹患している可能性のある集団に検査①重篤 ②経過の変化が期待できる ③有病率が高い
望ましい検査と現実
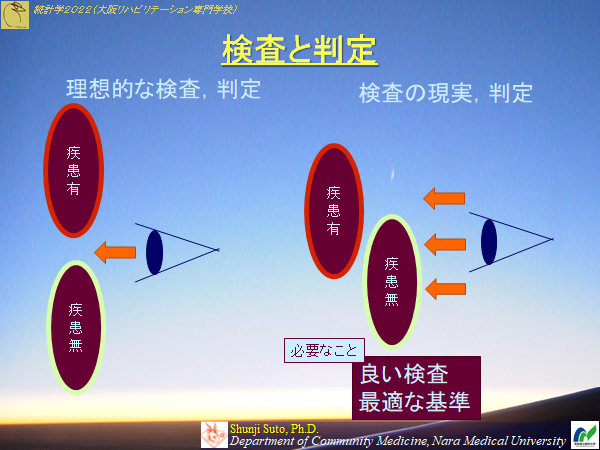
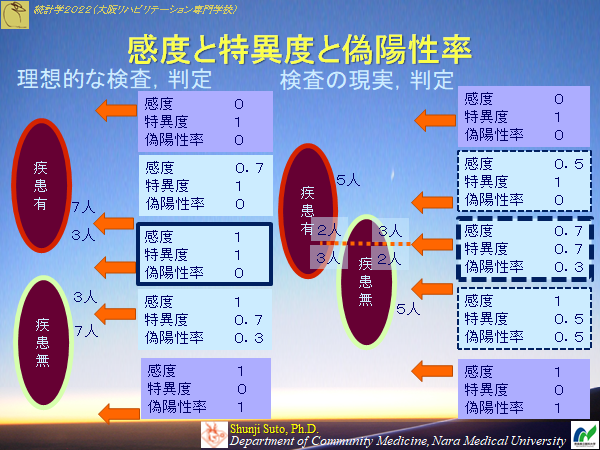
感度と特異度
感度=P(陽性|D) 疾患群における真陽性の割合偽陽性率=P(陽性|Dc) 非疾患群における偽陽性の割合
特異度=1-偽陽性率 非疾患群における真陰性の割合

予測値
有病率の影響を受ける
陽性的中率=P(D|陽性)
陰性的中率=P(Dc|陰性)
参考
File 3. 検査結果と有病率の関係(JMP-SAS Institute Inc.)
https://www.jmp.com/ja_jp/medical-statistics/column/non-series/test-results-prevalence.htmlROC曲線
判別度の分析感度と偽陽性率(1-特異度)を用いて曲線を描く

量的なデータも質的な評価も用いることが出来る.
例
| 疾患群 | 14.3 | 15.2 | 13.8 | 14.1 | 13.9 | 12.6 | 14.2 | 14.6 | 13.1 | 13.7 |
| 非疾患群 | 13.2 | 14.1 | 13.8 | 13.6 | 12.9 | 12.4 | 12.1 | 12.3 | 12.3 | 12.8 |
検査法の評価指標
尤度比
(陽性)尤度比=感度/偽陽性率 疾患のある人に対してどの程度検出できるか

AUC
ROCの曲線下面積面積が大きいほど特性が優れている
AUCの求め方は以下のように三角形と台形の面積を求めて足し合わせる事
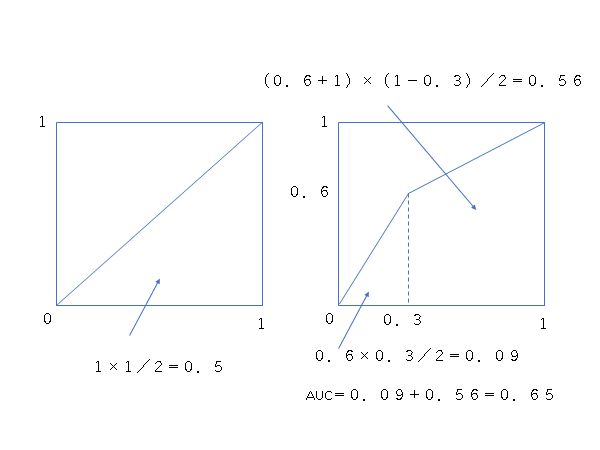
スクリーニングの効果判定におけるバイアス
リード・タイム・バイアス・・・早期に発見するとその分経過は長くなるレングス・バイアス・・・進行の速い病態は発見されにくい
セルフ・セレクション・バイアス・・・そもそも参加する人が偏っている
例題
次のマンモグラフィの検査結果からROC曲線を描き、AUCを(小数点以下2桁まで求め四捨五入)求め、カットオフ値の検討をせよ<参考>
森本 忠興,日本の乳癌検診の歴史と課題,日乳癌検診学会誌,18(3)211-231,2009
https://www.jstage.jst.go.jp/article/jjabcs/18/3/18_3_211/_article/references/-char/ja/
| 異常なし(1) | 良性(2) | 悪性を否定できない(3) | 悪性の疑い(4) | 悪性(5) | 計 | |
|---|---|---|---|---|---|---|
| 疾患群 | 0 | 4 | 14 | 12 | 10 | 40 |
| 非疾患群 | 20 | 20 | 12 | 8 | 0 | 60 |
課題
以下のデータと例題と比較しどちらの系がより優れているかAUCを求めて検討せよ| 異常なし(1) | 良性(2) | 悪性を否定できない(3) | 悪性の疑い(4) | 悪性(5) | 計 | |
|---|---|---|---|---|---|---|
| 疾患群 | 1 | 5 | 16 | 10 | 8 | 40 |
| 非疾患群 | 20 | 16 | 14 | 10 | 0 | 60 |