Medbb.net

奈良県立医科大学　生物統計学２０２４
（医学部医学科）

2024年度開講にあたって
https://medbb.net/education/2024init/
困った時，オンラインでのサポートやなにかありましたら以下からご連絡ください
私へ連絡・ｵﾝﾗｲﾝｵﾌｨｽｱﾜｰ予約

課題の提出状況については，出欠システムのところで表示するようにします．
9/1の1時限目　1回目の授業の課題
9/2の1時限目　2回目の授業の課題

評価は問題無しが○　ちょっと問題ありが△　未提出が×で入力しています．それぞれ（出席）（遅刻）（欠席）と表記されると思いますがご注意ください
授業への出席は開講期間の部分でご確認ください　開講期間外の9月分はあくまでも上記のように課題の提出状況を示していますので勘違いされない様よろしくお願いします

なお，例年例題について回答が欲しいという声があるのですが，授業中に示したとおりですのであらためて掲載はしておりません．

課題提出フォーム

https://forms.gle/GFakVm7EbcneXmkT8

授業メニュー

第01回　科学と統計

第02回　記述統計（１）尺度，度数，代表値

第03回　記述統計（２）散布度

第04回　推測統計（１）点推定(平均と分散)

第05回　推測統計（２）区間推定(二項分布と正規分布)

第06回　推測統計（３）平均値の区間推定(t分布)，検定の考え方

第07回　推測統計（４）パラメトリック検定

第08回　推測統計（５）ノンパラメトリック検定

第09回　【AB合同】中間まとめ（小テスト）

第10回　推測統計（６）度数に関する検定

第11回　相対リスク

第12回　ROC解析

第13回　相関係数，回帰分析

第14回　生存時間分析

第15回　【AB合同】まとめ

第01回　科学と統計

【GE-01-04-01】根拠に基づいた医療(EBM)の 5 つのステップを列挙できる
(教科書1章1,2)

授業の進め方

授業中は課題について廻りに相談せず各自で取り組んでください．不明点は私に質問してください．その内容をみなさんでシェア出来たらと思っています．
この授業は，２グループ制で行いますが，一部合同で行う回（第8回ミニテスト，第10回，第14回，15回）もありますのでご注意ください．
オフィスアワーは特に設けていないので，気になった時にTeamsからご連絡ください．

なぜ統計が必要なのか？

私たちはデータを取得して物事を判断し次の行動につなげている．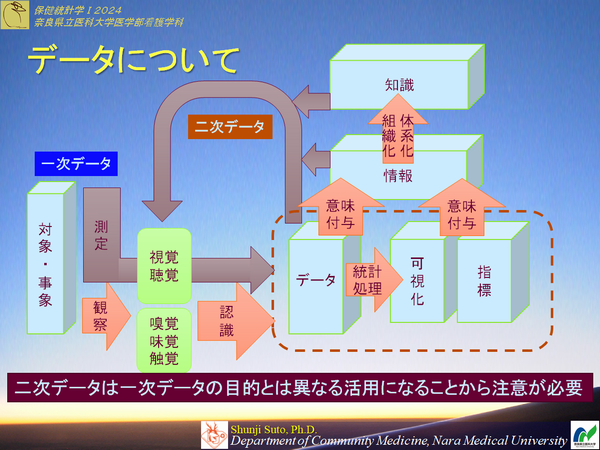

科学

科学が日常生活を豊かにしていることは明らかであるものの，科学者の想いによらない使い方もされたり，世の中全てを科学で説明できない

小学校学習指導要領（平成 29 年告示）解説　理科編（文部科学省）

科学が，それ以外の文化と区別される基本的な条件としては，実証性，再現性，客観性などが考えられる。
実証性とは，考えられた仮説が観察，実験などによって検討することができるという条件である。
再現性とは，仮説を観察，実験などを通して実証するとき，人や時間や場所を変えて複数回行っても同一の実験条件下では，同一の結果が得られるという条件である。
客観性とは，実証性や再現性という条件を満足することにより，多くの人々によって承認され，公認されるという条件である。

小学校学習指導要領解説（文部科学省）

https://www.mext.go.jp/a_menu/shotou/new-cs/1387014.htm

【理科編】小学校学習指導要領（平成29年告示）解説（文部科学省）

https://www.mext.go.jp/content/20211020-mxt_kyoiku02-100002607_05.pdf

実証性

検討することのできる仮説が無いことには始まらない

再現性

同一の実験条件では同一の結果が得られる

客観性

多くの人々に承認される

chatGPTによる実証性に関する質問

「検討することのできる仮説とは」

ChatGPT3.5
検討することのできる仮説は、研究や分析の目的に基づいて多岐にわたります。仮説とは、観測された現象を説明するための仮定や推測であり、実験やデータ分析を通じて検証可能でなければなりません。（以下略）

「検討することが出来ない仮説とは」

ChatGPT3.5（纏めると）
検討することができない仮説にはいくつかの特徴があります。科学的な文脈で、仮説は観察や実験を通じて検証可能でなければなりません。
検討が難しい仮説の特徴
検証不可能，曖昧な定義，超自然的な要素，因果関係の証明が不可能，非現実的な条件

EBM

Evidence-Based Medicine
根拠に基づいた医療
「根拠」・・・科学的根拠と表現されているケースも多い・・・（経験則だけに基づかないようにという意味合いを込めてというところかな）

医療提供における「根拠」以外の要素

意思決定における3要素・・・根拠，価値観，資源
価値観は人によってさまざま
現有（もしくは調達可能な）資源で出来ることしかできない

医療資源

（不足の観点からみる医療２．０β より）

「根拠に基づく医療」（EBM）を理解しよう（厚生労働省eJIM（イージム「統合医療」情報発信サイト））

https://www.ejim.ncgg.go.jp/public/hint2/c03.html

EBMの５つのステップ

1．問題の定式化

PICO
P(Patient)どのような患者さん（対象）なのか
I(Intervention)どのような介入を適用しようとしているのか
C(Comparison)介入しない場合（もしくは他の介入）と比較して
O(Outcome)どのような結果になるのだろうか

2．問題についての情報収集

掲げた問題に相当するような情報（世の中にある研究論文など）を探す

3．情報の批判的吟味

情報そのものがどの程度信頼出来るのか，効果があるのか．

4．情報の患者への適用

今回の患者さんと情報で得られた患者像を同じと見做し適用して良いか，問題あるのか

5．1～4 のstepの振り返り

研究の場合もPICO/PECO（E(Exposure) 治療などの介入ではなく曝露）で整理し目的を明確化します．
EBMはある患者さんに医療を適用するために情報を検索という流れですが，研究はある仮説を明らかにするために目的を明確化してデータ収集・分析となります．

南郷栄秀,Evidence-based medicine：診療現場でのプロブレムの解決法　日内会誌　106：2545～2551，2017

https://www.jstage.jst.go.jp/article/naika/106/12/106_2545/_article/-char/ja/

特集：EBMとEBH『公衆衛生研究』 第49巻 第4号 （2000年12月）

EBMの5ステップと意思決定の3要素

EBM1～3ステップが根拠の部分
根拠とする情報に実証性と再現性と客観性があったほうが良いというところは理解できるかと（つまり科学としての基本的な条件を満たしている方が良いだろう）
研究の方法によって，グレードが変わるのはそれらの要素が方法によって異なってくるので
ステップ4においては価値観と資源を含めた形となる

提出課題

月曜の課題はあなたが思う「らくたん」を漢字で示せ　ということになりました

— めどぶぶ (@medbb) April 6, 2024

１：あなたが思う「らくたん」を漢字で示せ
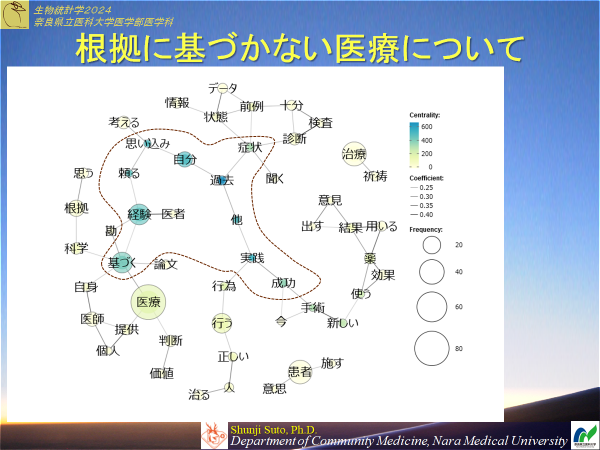
２：根拠に基づかない医療とはどのようなものかお考えを教えてください（短文で）
締め切りは授業日の22時00分までとします．
提出いただいた内容は例えば以下のような形で可視化した格好で示せたら良いなと思っています
（正直どうなるのやらわかりませんが）

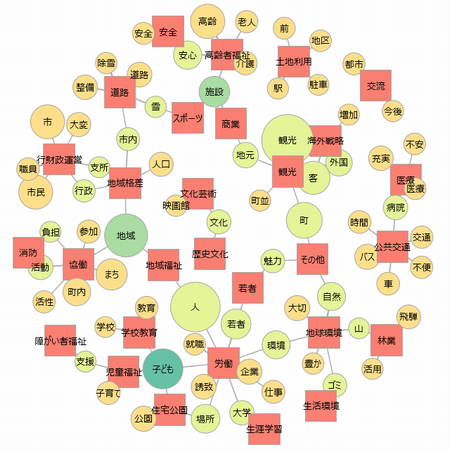
（保健医療分野におけるフューチャー・デザインの可能性 より）

課題の感想等

１）

漢字	度数	コメント
落胆	60	入学したのになぜ落ち込むのだろう．相談乗ります
落単	25	そのようなことにならないことを祈っています
楽単	21	楽しく学修し単位を取得してください
スポーツ実践	1	これを　らくたん　と読むのか．油断しない様受講して
楽探	1	楽しく探究できるよう私も頑張ります
楽胆	1	楽しんでいただけるのならば何より．でも違うのかもしれないな．相談乗ります
健康	1	体調の問題で無ければ良いのですが．相談乗ります
落単します	1	その宣言を現実にならないようにするのが私の役目です．前向きに取り組みましょう

＜参考＞楽胆（人間詩人　小説家になろう）
https://ncode.syosetu.com/n2975fr/

２）

第02回　記述統計（１）尺度，度数，代表値

【SO-02-03-01】尺度（間隔、比、順序、名義）について説明できる。
(教科書2章1)

統計に用いるデータ

基本どのようなデータでも統計処理は出来る
出来ないのは，どのようなデータであっても一つしか存在しない時

データについて

レコード

症例，個体，被験者単位でまとめられたデータの塊．表の場合一行にその症例のすべてのデータを記していたらそれがレコード

変数（変量）

データの項目名のこと

データ

観測値や測定値のこと（数値）だけでなく性別など文字の場合もある．
コンピュータ処理するとき，文字だと扱いにくい時があるのでその時は数字に置き換える（→コード変換）
例えば都道府県名であれば　北海道→０１　青森県→０２　奈良県→２９
全国地方公共団体コードの上二桁＝都道府県番号

＜参考＞全国地方公共団体コード（総務省） https://www.soumu.go.jp/denshijiti/code.html

都道府県番号の順序を用いて説明する事柄は存在しない．一方，文字で順列の存在するもの（松　竹　梅）はその法則にしたがった番号を振ることがあるので注意

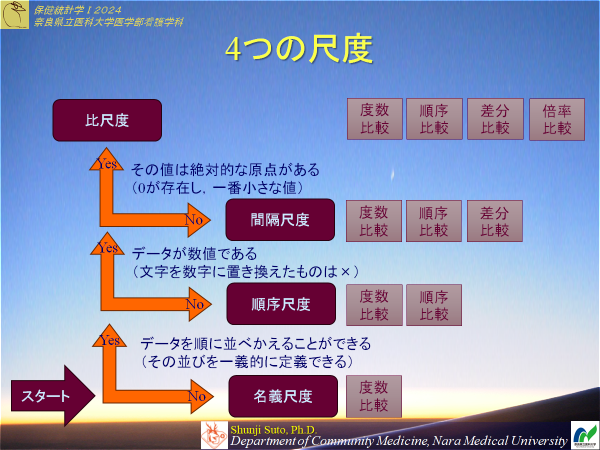
変量(データ)の分類

変量は様々なものがあるがそれらの性質をとりまとめ分類することが出来る。
それぞれを尺度と呼び、4つに分類するのが一般的である
１分類尺度（名義尺度）
２順序尺度
３間隔尺度
４比尺度（比例）（比率）

１，２を質的変量（定性的）
３，４を量的変量（定量的）
性質としては上位互換性があり
４＞３＞２＞１

統計量

取りまとめたものを「量で」示したもの．質的変数であっても度数（個数，人数など数えるもの）については「量」として示すことが出来る

度数

どのようなデータでも度数を示すことは可能

度数分布表

この授業では量的変量の度数分布表を作成する場合　A～B　は　A以上B未満として取り扱う
　 それぞれのデータ（変量）の数（出現頻度）をまとめたもの
変量が名義尺度の時は多い順（お作法として。但しその他を出すなら一番最後）
順序尺度以降であれば順（名義尺度でも比較のためにお作法を破ることはある）
度数　　・・・出現頻度
相対度数・・・総出現頻度を1（100%）としたときのそのぞれの度数のしめる割合
累積度数・・・上位の変量の度数もあわせた度数
累積相対度数・・・累積度数の相対版

例題２－１

以下の店名別のみかんの売り上げデータより度数分布表を作成せよ

日付	店名	数量（箱）
9月1日	奈良本店	１４００
9月1日	大和郡山店	７００
9月1日	大和高田店	４５０
9月2日	奈良本店	１０００
9月2日	大和郡山店	９００
9月2日	大和高田店	１１００
9月3日	奈良本店	１６００
9月3日	大和郡山店	４００
9月3日	大和高田店	８５０

店名	度数	相対度数	累積度数	累積相対度数
				１．００
計		１．００	-----	-----

量的変数の度数分布表

量的変数の場合はその数値だけで度数を積み上げようにもなかなか上手くいかない場合がある．
血圧　163.5mmHg　164.2mmHg　162.5mmHg・・・どれも度数を積み上げられない　→　区間を設定する

「A～B」は「A以上B未満」と読む格好と思っていたが，分野などによって違うようです 「A以上B以下」のようにどちらの階級にも属してしまう可能性のある設定はしないように．

階級	階級値	度数	相対度数	累積度数	累積相対度数
130～140	135
140～150	145
150～160	155
160～170	165
170～180	175
計			-----	-----

度数分布図

質的変数・・・縦棒グラフ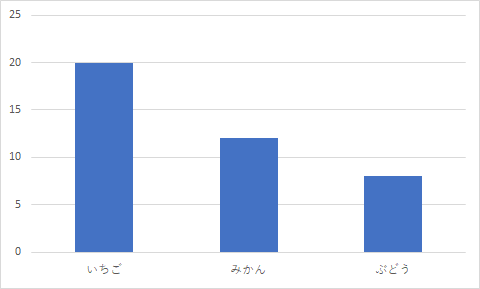

量的変数・・・ヒストグラム

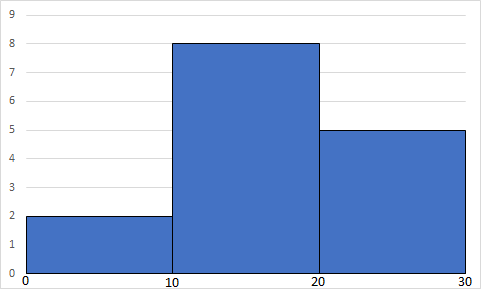
棒の間隔が無いのは値が連続している状態であるが故
普通の棒グラフは棒の長さが度数を示すが，ヒストグラムは棒の面積が度数を示す

「階級の幅を等しくすること」と説明している場合があるが，それは幅が変わると高さが変わる故で，実際にはそのような区間設定はよくある

以下の参考資料に区間幅の異なるヒストグラムについても説明なされているのでよろしければごらんください

ヒストグラムーなるほど統計学園（総務省統計局） https://www.stat.go.jp/naruhodo/4_graph/shokyu/histogram.html

記述統計量（代表値）

代表値と散布度からなる．←駅伝やマラソンの実況中継はこれらを利用しているから状況がわかる

平均（Mean）

算術平均
いわゆる割り勘．xbar=1/n(x1+x2+･･･+xn)
欠点：外れ値があると平均値は分布の中心位置を示さない（←それって代表的な値？？）
　→　対処法：外れ値を取り除くか中央値を使うか
幾何平均（相乗平均）
全て掛け合わせて累乗根をとる
加重平均
重みづけ平均
例えば　ミニテストと期末試験の平均をとる　→　そのままの平均で良いの？
度数分布表を用いた平均もこの方法・・・Σ（階級値×階級の度数）／ｎ

中央値

昇順に並べたときに，真ん中の順番のデータ（変数）の値
データの数が偶数だと真ん中のデータは二つになるのでそれらの平均値

最頻値

最も個数が多いデータの値
最頻値は複数存在する場合がある→二峰性

平均値と中央値の考え方の違い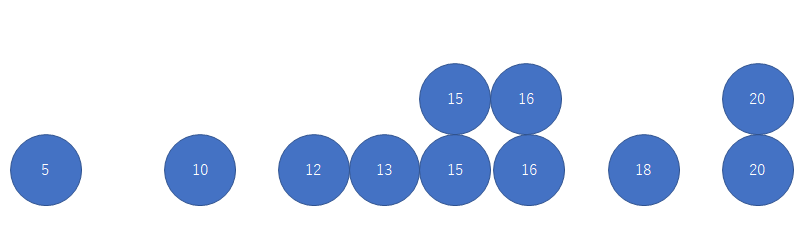 平均値（14.55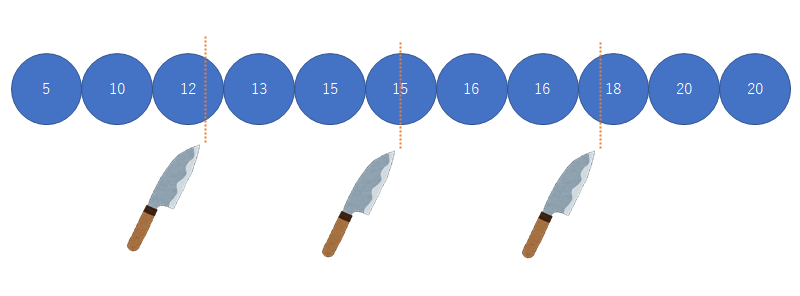） こちらは分布なんて関係なく中央値（15） データの分布に依存する（パラメトリック）＝平均値　と　データの分布に依存しない（ノンパラメトリック）＝中央値，最頻値の関係がわかるかなと思います 例えば５が０に変わってしまうと平均値は大きく変わりますが，中央値は変わりません パラメトリック・・・数値に依存する（数値の分布によって値が影響を受ける）というとイメージしやすいのかな？

例題２－２

以下の個票データより

ID	身長(cm)
1	163
2	158
3	166
4	155
5	165
6	168
7	156
8	161
9	150
10	167
11	162

階級	階級値	度数	相対度数	累積度数	累積相対度数
150～155
155～160
160～165
165～170
170～175
計			-----	-----

１）平均値（個票データ），中央値，最頻値を求めよ
２）平均値よりも中央値が大きくなる時のデータ分布の特徴を述べよ
３）平均値よりも最頻値が大きくなる時のデータ分布の特徴を述べよ
４）個票データによる平均値よりも度数分布表による平均値の方が大きくなる時のデータ分布の特徴を述べよ
５）今回の度数分布表では，個票データにより求めた平均値と度数分布表による平均値に最大どの程度の差が生ずるか述べよ

Aクラスは１）の解説まで
共通）度数分布表による平均値は階級値の話もしながら解説で

提出課題

本日の授業を受講したうえで，以下の2つの質問
１．理解できた内容，理解できなかった内容について
２．本日の授業の内容に関する質問（内容が概ね理解できているのであれば空欄でも可です）
を締切までに提出の事
締切は授業日翌日朝10時までとする

課題の感想等

氏名の記入など

学籍番号についてアルファベット不要などのお願い（含む半角での学籍番号）をお願いします．
学籍番号欄に氏名を入れている方もいるのですが，間違えないよう．
データの前処理で無用な時間が発生しないようにするためです．ご協力ください

本日の講義内容は何を目的としていたのか？

Ans.データを適切な形で取り扱うため

有効数字の桁数＝有効桁数について

込み入った話はブログで説明しようとしておりますが下書き中．以下あっさりと
有効桁数は値が信頼出来る値の桁数を示します．
ポイントは １）指数表記すると有効桁数が把握しやすくなる
１．３３×１０^３＝１３３０　（有効桁数は3桁）Excelでは1.33E+03と表記します
２）間隔尺度(＋－)の世界と比例尺度(×÷)では取り扱いの考え方が違うというところでしょうか．
説明用のデータは以下ですが有効数字で示した状態です
A,48.8kg　身長1.63m
B,53.25kg　身長1.721m

足し算引き算

こちらは有効桁数そのものではなく有効数字の位に基づいて求める形になります
（計算した数値の中でそれぞれ有効な桁の一番低い位の中で一番高いものが，その計算における信頼できる最も低い位となります）
ABの二人の体重を合算すると48.8+53.25=102.05kgとなります．
Aの有効な桁の一番低い位は少数1桁，Bは少数2桁ですので，この計算では少数1桁となります．
有効な桁から外れた桁の端数（丸め）処理ですが，計算後に行う方が丸め誤差の発生を抑えることが出来ます
四捨五入で行った場合102.05→102.1kgとなります（有効桁数4桁）
ちなみにBからAの身長を引いた場合は1.721-1.63=0.091となりますが，有効数字は0.09kgとなります（有効桁数1桁 9×10^-2）

掛け算割り算

こちらは有効桁数そのもので求める形になります
（計算した数値の中でそれぞれ有効数値の一番少ないものが結果の有効桁数になります）
AのBMIは計算すると18.36727013　有効桁数は全て3桁なので端数処理で四捨五入すると18.4
BのBMIは計算すると17.97868285　有効桁数は全て4桁なので端数処理で四捨五入すると17.98
AとBの身長を掛け合わせると2.80523　有効桁数が一番少ないのはAの3桁なので四捨五入すると2.81

感謝のお言葉（お礼する相手は私ではなく，私の講義を受講している学生さん皆さんに）

帰宅が夜10時頃で疲弊してすぐ意識を失ったので、提出期限を翌朝10時にしてもらわなかったら確実に未提出でした。ありがとうございます。

尺度による捉え方

比と順序では変量が異なるのに、どちらの方が有能であるのかを比較することは可能なの？
Ans.用いている単位系が何を示したものかによりますし，どのように解釈するのかによります

度数とは

例題2-1のみかんの売上個数は変数では？
Ans.仰る通りで，一日の売上個数は複数の伝票からなっており，その伝票の中で・・・

出現頻度とは

度数が出現頻度と書いており，出現頻度は「頻度」という言葉があったので，確率のような考え方だと思いました．出現頻度の「頻度」は，どういうことを意味しているのでしょうか？
Ans.頻度って度数としてつかっていますが，確かに頻度が高い　となると　確率の事を示しますよね（単位時間当たりの度数が多い／少ない　という形で）

累積度数はなんのため

Ans.特に名義尺度の時によく使う印象ですが，自動車の会社別売り上げ台数とか

感想（なるほどと思った）

高校数学のデータの分析を多少深めた内容

Excelについて

今回はExcelのsumなどを使って楽に計算しましたが、試験等でこれを手計算（または電卓）でしないといけないと思うとつらい
Ans.授業中に答えを表示するためにエクセルで計算して表示していますが，皆さんは手計算で行ったほうが良いかなと思っていますが（試験はエクセル禁止なので），授業中エクセルで行うことを妨げておりません．
そこでエクセルの関数などの解説についてのご要望もいくらか頂いておりますが，述べた通り授業の内容と離れてしまうものの，ある程度ニーズ（知りたい）があるように思います．
無論本授業と離れるので，一般的なオンライン講義の形態で参加したい人だけ参加するという恰好が落ち着くかなと思っています
行うとしたらオンラインでどこかの時間でExcel初級講座（他学の受講生も参加できるようにするかも）
ちなみに過去は統計の基礎（ちょうど皆さんが習う部分）というのを同様に行っています．授業外で一般の方も含む可能性があるのでpeatixで管理しています．
以下ご参考までに
統計学２０２３
https://medbb.net/education/medbbstat2023/index.php

第03回　記述統計（２）散布度

【SO-02-03-02】データの分布（欠損値を含む）について説明できる。
(教科書2章1)
「範囲」とはある点Aからある点Bとの間をさす

範囲

範囲

一般的に範囲と言えば　最大値と最小値の差　のことを指す

例題３－１

例題２－２の個票データより，範囲を求めよ

例題３－２

散布度として範囲を用いることの利点と欠点を考えよ

四分位範囲

順序尺度の性質を用いた散布度
小さい順（昇順）に並べて集団を4等分
分割する所の値を小さい方から第１四分位数（Q1），第２四分位数（Q2）＝中央値，第３四分位数（Q3）
また第１四分位数は25%タイル値，第２四分位数＝中央値＝50%タイル値，第３四分位数＝75%タイル値とも呼ばれます
大きい方が第３四分位数なのですが，間違える方も一定数いますが100%タイル値＝最大値ということを理解していたら大丈夫でしょう
四分位範囲IQR(interquartile range)=Q3-Q1
四分位数の算出方法は数多くあります
高校数学で習われたものは文部科学省が推奨した方式で，高校数学以外では見掛けない方法です．
一番わかりやすい四分位数の出し方はヒンジ値になります

以下のブログを見ていただくと数種類出来てしまうのも頷けるかと思います

ダンゴ包丁理論（tukeyのヒンジ）（Medbb's blog）
https://medbb.hatenablog.com/entry/2020/12/12/091240
考え方としては理解しやすいと思いますがtukeyのヒンジとは少し値が異なるケースもあります

＜参考＞四分位数の定義（奥村 晴彦 (Haruhiko Okumura)）
https://okumuralab.org/~okumura/stat/quartile.html
＜参考＞■四分位数の定義－教科書の内容に関するQ＆A（数研通信（78号）数研出版）
https://www.chart.co.jp/subject/sugaku/suken_tsushin/78/78-10.pdf

箱ひげ図

四分位範囲をグラフ化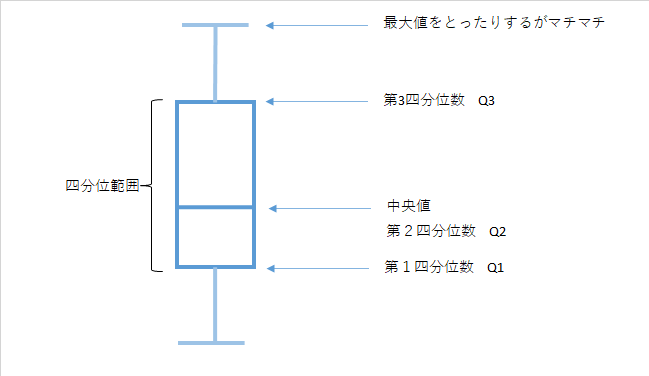

例題３－２

散布度として範囲と四分位範囲を比較した時それぞれの利点と欠点について考えよ

偏差

「偏差」とはある点と基準点とのズレをさす
「偏差」とだけ記述されてると基準点は平均値として捉えられるケースが多い

四分位偏差

順序尺度の性質を用いた散布度
QD(quartile deviation)=IQR/2=(Q3-Q1)/2
四分位範囲を2で割ると求められるが，意味的には第3四分位数と第2四分位数の偏差と第2四分位数と第1四分位数の偏差の算術平均
QD=((Q3-Q2)+(Q2-Q1))/2=(Q3-Q1)/2

(平均値との)偏差

集団の平均値と個々の値の偏差を求めその平均をとることでその集団のバラツキ具合を算出

例題３－３

各々の値について，その集団からもとめた平均値との偏差を求めた場合，その偏差の平均は必ず０になる．証明せよ

分散

間隔尺度の性質を用いた散布度
平均値から求めた偏差の平均は常に０になってしまうので意味が無い．
平均値から求めた偏差の平均を求めればよいが，計算が面倒だった模様です．（近年PCを使えば簡単なので　と思わないように）
分散は偏差平方の算術平均

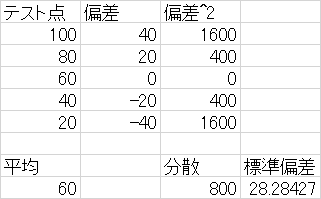
利点は，偏差を基にした散布度を算出できること
欠点は，求めた散布度の単位が対象とするものを二乗した格好になっている

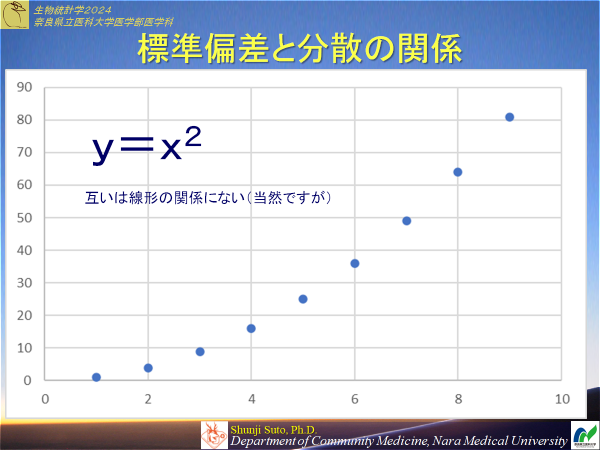
標準偏差

間隔尺度の性質を用いた散布度
利点：対象とする集団の平均値と同じ単位になっている．
欠点：あくまでも平方根を用いて求めているので注意する点がある
（分散と標準偏差は線形の関係に無い）

例題３－３

ある集団Aテストの点を平均と分散を求めたところそれぞれ６０点と１６だった．
集団Bも同様に求めたところ６７点と４だった．
集団Aの得点のバラツキ具合は集団Bと比べたらどの程度大きいか示せ．

例題３－４

例題2－2のデータより 散布度（四分位範囲，四分位偏差，分散，標準偏差）を求めよ．
なお四分位数については，文部科学省の示した方法及び，tukeyのヒンジ値両方で求めること

想定していないデータ

大量にデータを取り扱うと様々な理由（入力ミス，測定していない，装置の利用方法を誤る）で想定外のデータが出現する
無論想定が甘いと正しいデータの場合もあり得る
とりまとめると異常値と欠損値についてはデータの取り扱いについて考慮しなくてはならない

外れ値

想定している範囲外のデータを指す

異常値

外れ値の中で人為的なミスや機器の故障など測定や入力が適切にされていないためにおこるもの

欠損値

値が欠損している状態で，測定できなかった場合や回答してもらえなかっただけではなく異常値と同様に人為的なミスや機器の故障など測定や入力が適切にされていないためにおこったものを含む

＜参考＞データクレンジング（用語集　bodais）
https://bodais.com/info/glossary/id0900000272

例題３－５

測定したデータから記述統計量（度数，代表値，散布度）をそれぞれ用いることで，どのような想定しないデータを検出することが可能か考えよ

本日のポイント．雑談含む

（異常値の話の件で）米騒動

＜参考＞今年の共通テストの数学は…（網重塾）
https://amishige-jyuku.amebaownd.com/posts/31726305/
（四分位範囲の件で）試験に出すとしたらtukeyが良いか文部科学省が良いか
（最初の入りあたりで）部分点の話，答えそのものより，考え方のところが重要ですよね．だって新たな知見を求めていくわけですから
（例題のあたりで）ダンゴ包丁は四分位数の考え方を理解するためのものということで（簡単に分かりやすく互換性を持たせるのって難しい）
（最後時間が無くなって）例題２－２の解説時間が無くてできませんです

提出課題

本日の授業を受講したうえで，以下の2つの質問
１．理解できた内容，理解できなかった内容について
２．本日の授業の内容に関する質問（内容が概ね理解できているのであれば空欄でも可です）
を締切までに提出の事
締切は授業日翌日朝10時までとする

課題の感想等

締切を守れない方は，どのようにしたら管理できるのか工夫しておいてください
私はgoogleカレンダーで一括管理するのが合う様で，さまざまな締め切りを乗り切っています

ダンゴ包丁理論

あくまでも，四分位数の話を分かりやすく説明するために考えたもので一般では使われておりませんのでご注意ください
試験で使うならばというのは文科省派が多かったので，出題するときはそのようにします
四分位偏差の意味がようやく理解できた。結局ダンゴが使えるかどうかがわからないダンゴは意味の理解には非常に有効ですがダンゴはtukey近似にはなりますが周期的に値が異なるんですよねぇ

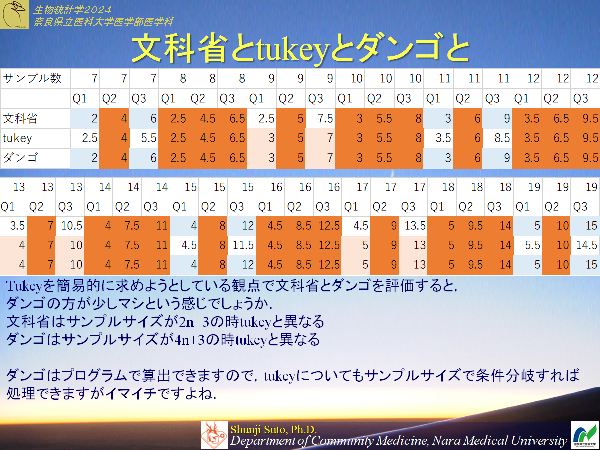
tukeyのデータを中央値から対称にジグザグに並べる方法がよくわからない改めて上の例で（番号と数値一緒にしています）

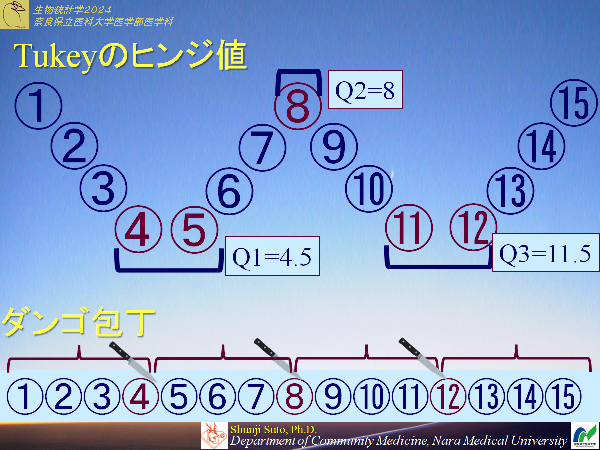
四分位数にはいろんな定義がある　なぜ四分位数の求め方を統一しないダンゴを包丁で説明したのは４つに分割して値を求めるにしても色々方法があって当然と思っていただけたらというところです
医学領域においてもこのような話はあります

＜参考＞ 妊婦健診の際の計測について（２０２２年８月）（医療法人慈光会岡本産婦人科）
https://www.okamoto-obgy.jp/news-2022.html#n22-08

高校数学で習った四分位範囲が，本来のものと・・・本来という部分でも多くの算出方法があるわけでして，重要なのは外れ値の影響を受けない範囲の出し方というところはみな共通だと思います
四分位数は教科書に載っているものが絶対的なものだと思っていた世の中に絶対的なものは存在しないという考え方が「科学」と捉えています

偏差の平均はなぜ常にゼロ

偏差の平均が0になるのは頭ではわかるけど頭の中を整理したうえで表現して伝えるのが社会人の使命．皆さんの領域ではいずれ臨床や研究を通して自分しか知らない新たな知見に辿りつくと思います．その時にあれこれ考えながら分かりやすく伝えるということが必要になります．何を計算しているのかということを整理すると証明（説明）の仕方が出てくると思いますが重要なのは，自分であれこれ考えることでしょうか？自身の思考のクセなどがわかるかもしれません．それは他者が教えることはかなり困難で人生の財産になるものです

第04回　推測統計（１）点推定(平均と分散)

(教科書2章1)
偏った推定はよろしくない（あたらないから）
特に，計算の過程で偏ってしまうとかなりよろしくない

推定することについて

記述統計では，対象とする集団そのものの可視化が目的
推測統計では，対象とする集団は全体の中の一部（サンプル）という捉え方で，サンプルから全体像を推し測ることを目的
世の中で全てを把握するというのはかなり難しい

国勢調査

日本全国に住んでいられる方を対象にした静態調査
かなりコストをかけているが，それでも100%の回収率は難しい

＜参考＞
令和２年国勢調査の概要（総務省統計局）
https://www.stat.go.jp/data/kokusei/2020/gaiyou.html
2020年国勢調査の回答状況における都市-農村格差（*山本 涼子, 埴淵 知哉, 山内 昌和　2021年度日本地理学会春季学術大会要旨集）
https://www.jstage.jst.go.jp/article/ajg/2021s/0/2021s_30/_article/-char/ja/

点推定はあたらない

針の穴に糸をとおすような話

記号について

推定の話になると記号の取り扱いで混乱するのでここで整理しておきます．
分かりやすさを優先して整理したので，皆さんの使っている教科書などの表記は＜参考＞の論文を確認し読み替えください
μ・・・集団全体（母集団）の算術平均＝母平均
σ^2・・・集団全体（母集団）の分散＝母分散
σ・・・集団全体（母集団）の標準偏差＝母標準偏差

xbar・・・集団の一部（標本）の算術平均＝標本平均＝母平均の不偏推定量
s^2・・・集団の一部（標本）より求めた母集団の分散の推定量=不偏分散（母分散の不偏推定量）
s・・・集団の一部（標本）より求めた不偏分散よりもとめた標準偏差＝母標準偏差の推定量

参考

統計学テキストの「分散」の表記に関する調査（札幌学院大学総合研究所紀要　巻 1, p. 1-10, 発行日 2014-03-31）
https://sgul.repo.nii.ac.jp/records/1807

母集団と標本

母集団

対象としている集団の全体のこと
無限母集団と有限母集団がある

標本

対象としている集団の一部
偏ってしまうことに注意
例）森で取れた昆虫の標本を作成する際、どうしても森全体の昆虫の分布から偏ってしまう

取り扱う標本について

母集団は20000人の収縮期血圧データ（整数）

母集団のヒストグラム

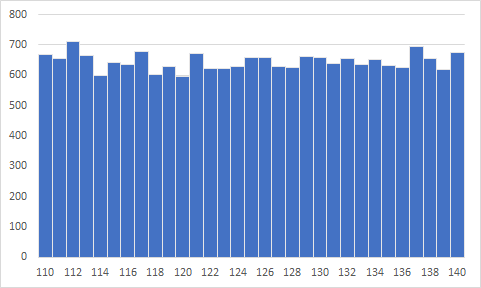
その集団の一部を抽出したものが標本

＜注意＞上記のデータはサイコロの目が均等にでるのと同様に以下のように収縮期血圧データは110から140まで均等に出現しています．
実際にある集団に対して収縮期血圧を測定するとその血圧データの分布はそのような形になりません
諸々の事情（説明を理解しやすく）を含めて設定したのですが実際とは異なる振る舞いをしているであろうことだけ承知しておいてください．

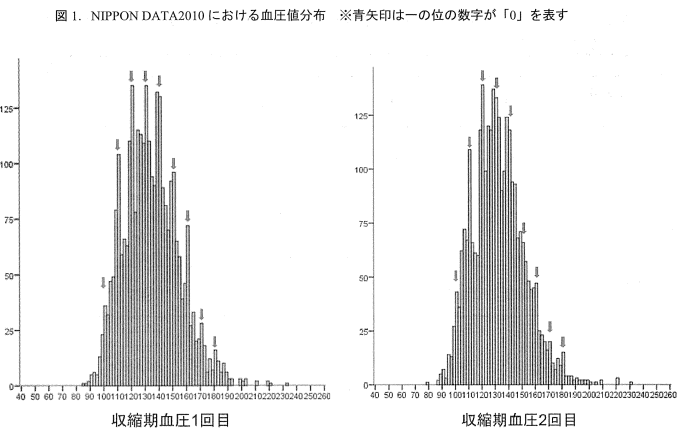
日本人の健康・栄養状態のモニタリングを目的とした国民健康・栄養調査のあり方に関する研究（厚生労働科学研究成果データベース）（https://mhlw-grants.niph.go.jp/project/23935）を加工して作成

＜参考＞日本人の健康・栄養状態のモニタリングを目的とした国民健康・栄養調査のあり方に関する研究（厚生労働科学研究成果データベース）
https://mhlw-grants.niph.go.jp/project/23935
の平成24年度～26年度　総合研究報告書のP108図1の部分を取り出して加工したものが上記になります
https://mhlw-grants.niph.go.jp/system/files/2014/143031/201412017B/201412017B0006.pdf

母平均の点推定

得られた標本より求めた平均をそのまま母集団の推定値とする

例題４－１）

以下の標本より母集団の平均値（母平均）を推定せよ

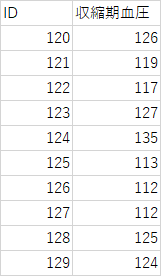
利点

計算が容易
平均値の場合，計算式が母集団全体の値を求める時と標本から推定する時と同じで良い

欠点

必ずしも推定値が実際と一致するわけではない・・・むしろ外れて当然
サンプルサイズ１０の時（母集団から２０００の標本が作成できる）のヒストグラム

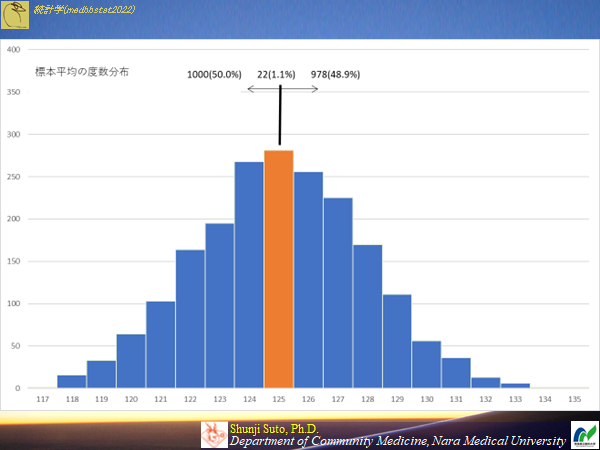
ピッタシ一致するのはサンプルサイズ10の時で1.1%（98.9%はハズレ）

推定の精度を上げるためには

標本数を大きくすればよい・・・測定を繰り返して行いその平均をとると精度は上がる
サンプルサイズを１００にした時の（母集団から２００の標本が作成できる）のヒストグラム

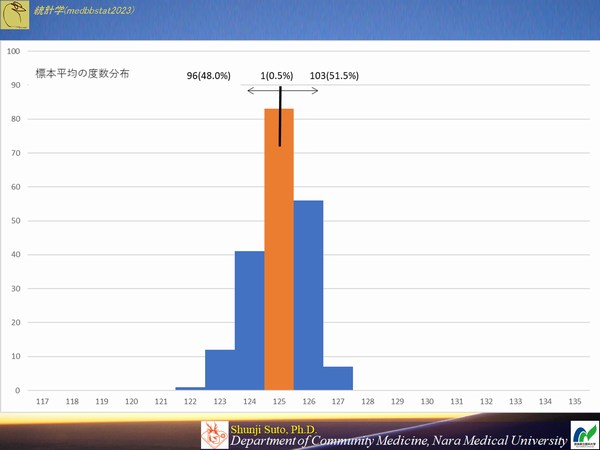
精度は上がるものの，ピッタシ一致する確率も上がるとは限らない

例題４－２

結局一つの値で示す点推定はなかなかピッタシ一致しない．ならば幅を持たせた区間推定は最大何パーセントまであてることが可能か？

母分散の点推定

母分散の推定は一味違う

例題４－３）

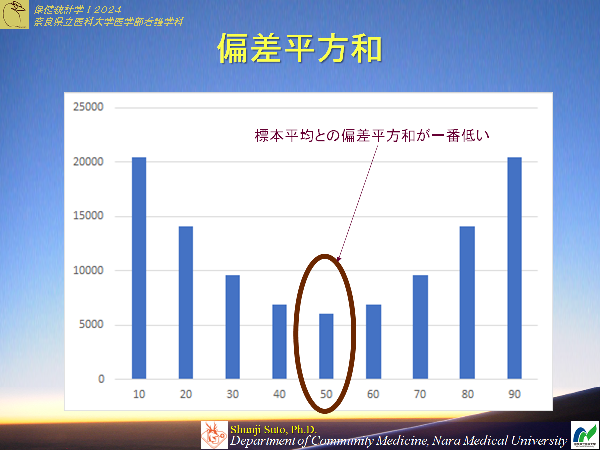
例題４－１）のデータと例題４－１）で求めた母平均の推定値との偏差を求め，偏差和（全て足し合わすこと）を求めよ．そして偏差平方和も求めよ
例題４－１）のデータと私だけが知っている母平均（125.0）との偏差を求め，偏差和を求めよ．そして偏差平方和も求め，それぞれ比較せよ

標本の平均を用いサンプルサイズ１０の時（母集団から２０００の標本が作成できる）のヒストグラム

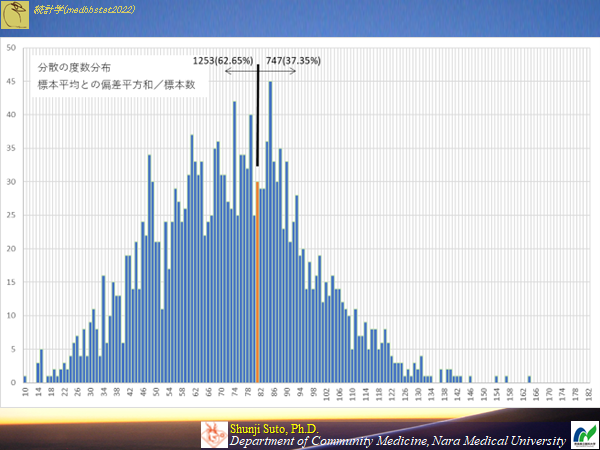
低めの値が多くなる傾向で偏っている．

母集団の平均（本来知る由もない）を用いサンプルサイズ１０の時（母集団から２０００の標本が作成できる）のヒストグラム

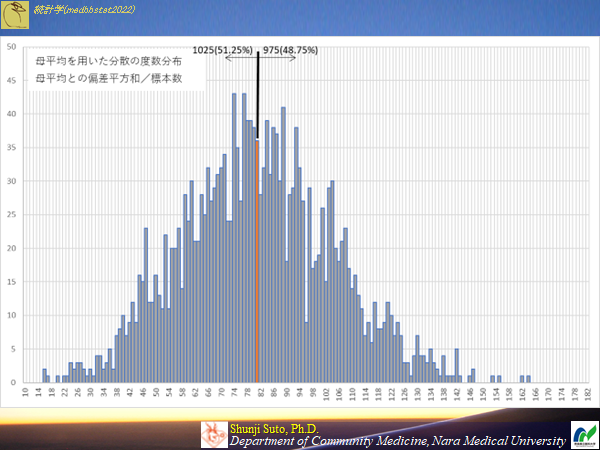
偏った推定にならないものの，本来知る由もない母平均を使えるわけがない（そもそも母数知っているなら推定は不要でしょう）

不偏分散

標本の平均を用いて母分散の推定を行う．
母平均と標本平均は（ほぼ）異なるので，母平均と標本平均の差も考慮して分散を求めたもの
（無論母平均は分からないが母平均と標本平均の差を考慮している）
s^2=Σ(Xi-Xbar)^2／(n-1)
nで除するよりn-1で除したほうが，値が大きくなるのは当然なので，低めの値が出るのなら少し分母を小さくした方が大きくなるのは理解できるが（ケーキを3人で分けるのか4人で分けるのか）なぜ１引くだけ？？となると思います

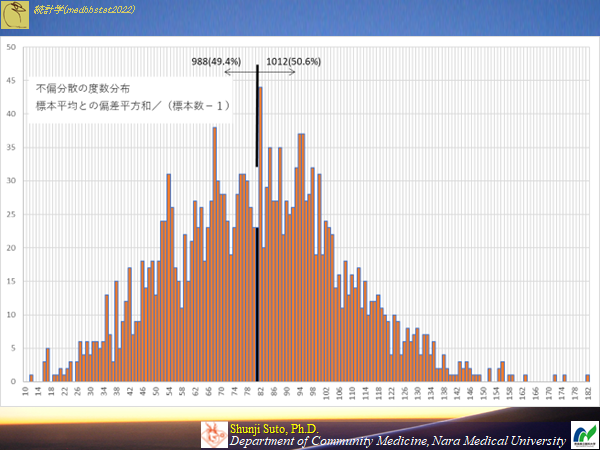
＜参考＞ 不偏分散は何故nではなく（n-1）で除するのか（生物統計学2018奈良医大）
https://medbb.net/education/nmubiostat2018/index.html#VAR

例題４－４

例題４－１）のデータより母集団全体の平均値および分散と標準偏差の推定値を求めよ

不偏分散より求めた標準偏差は不偏推定量なのだろうか？

上記の不偏分散のヒストグラムを標準偏差にして作成したもの

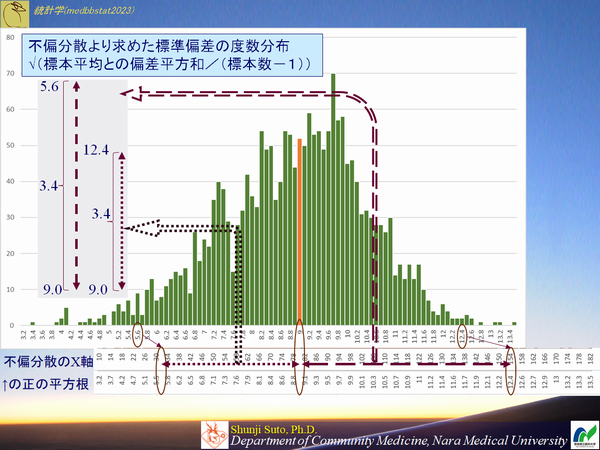
＜参考＞不偏分散の正の平方根は不偏標準偏差でよろしいのか（よろしくない）（Medbb's blog）
https://medbb.hatenablog.com/entry/2024/01/09/232914

平均値の区間推定に向けて

母集団の平均値の点推定値はほぼ一致しない（あたらない）ことがわかった
100%あたる区間推定はもはや意味をなさないことはご存じの通り
母集団の平均の推定値（つまり標本の平均）を用いて母標準偏差の推定値（不偏分散の正の平方根）で幅をとれば１００％ではないが区間推定が出来そう
一方，標本数が増えると標本平均の分布は狭まることは確認している．果たして不偏分散は標本数が増えるとどのような挙動になるのだろう

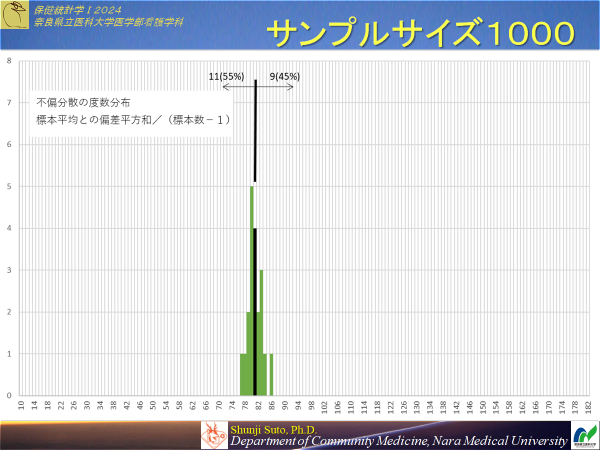
と，サンプルサイズを10→1000に増やすと不偏分散の分布の幅は狭くなったものの，不偏分散が小さくなるわけではない・・・（平均値と同様に精度が上がっただけ）

平均値のバラツキ具合はサンプルサイズが大きくなると減少するが，不偏分散（に基づく標準偏差）は減少しないのでサンプルサイズが大きくなると減少する散布度が必要となる

提出課題

本日の授業を受講したうえで，以下の2つの質問
１．理解できた内容，理解できなかった内容について
２．本日の授業の内容に関する質問（内容が概ね理解できているのであれば空欄でも可です）
を締切までに提出の事
締切は授業日翌日朝10時までとする

課題の回答まとめ

不偏分散の件みなさん考えてソースを探されて試されたりした方もおられました．またご自分で数式をまとめたかたもおられました．授業のページで公開するか別の形にするか考え中です
高校時代のことがどの程度知識となっているのか，バラツキ具合が出てきているなと思いながらです
高校の時に共通テストのために勉強した内容　という形で既に理解済みの方もおられました
覚える（パスワードのように）から理解（何故そのよういになるのか）に受講生全員がシフトすることが求められる大学初年次科目としての役割を果たせているのかなと思いながらまとめております．

上手に理解している系

ひとつずつ意味を考えて計算をすると案外簡単
分散が母集団の分散よりも小さくなることがとても分かりやすかった

予想的中

今回から難しくなりました

不偏分散

不偏分散が何かを知れたが、どういう場合に使うかが分からない標本から求めたものであればその母集団の分散を推定するとき
気になったので不偏分散は何故nではなく（n-1）で除するのかの計算を自分でもやって確認してみました
不偏分散を求める際に(n-1)で除算する意味（大きくすること）は非常によく分かった
非常にうまく数式にまとめられた方がおられたので，こちらに載せたいのですがご本人と相談してからにするので少しお待ちください

講義室関連

後ろに座っている=授業聞いていないと解釈されていないかが不安　授業を理解しているかはテストで確認しています．聞いているか否かそのものは受講態度に含まれますが着席場所のみでの判断は難しいように思います．場所近辺の騒音状況いかがでしょうか
なお，授業に明らかに参加していない学生，もしくは妨害している学生など受講態度に問題のある学生がいた場合の対応につきましては，既に大学側に取り扱い（当該学生への告知方法など）について照会している状況です

誤解しているかも

そもそも母平均とは何なのかが分からない　取り扱っている集団は標本（母集団の一部）で母平均とは母集団全体の平均値のことです．この言葉が無いので以下のような形になるのだろうと思います
今回の例題４－３の母平均は１２１を用いるのか１２５を用いるのか分からなかった　例題4-3で意図を含めて両方使った計算をしたともいます（一応125という数字は皆さんは使えない数字（知らないので）ですが）
今回の例題４－４の母平均は１２１を用いるのか１２５を用いるのか分からなかった　授業中説明したように思いますが「推定値を求めよ」の時点で125という数字は知らない数字となります
グラフが平均に対して右寄りのときにー１すると先生は言っていたが 分散の話ですよね．私はそのような趣旨の説明をしたつもりはありませんが，母分散に対して標本から求めた分散は小さくなるという話のことかなと思います

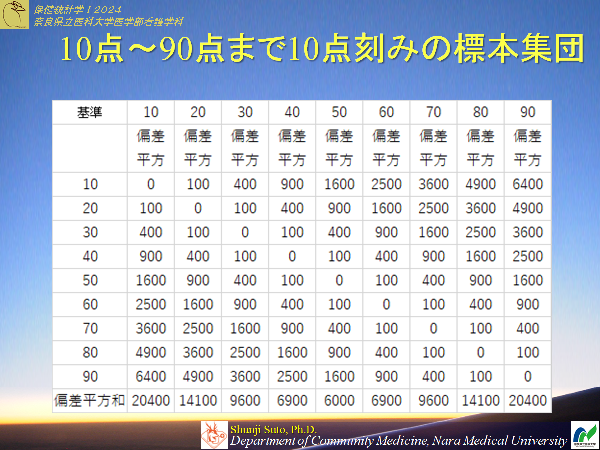
感想

授業を聞いていなければ授業に基づく理解は当然出来ないのですが，これまでの知識（高校生活）で既に獲得している方は，ミニテストでは授業を（聞く／聞かないによらず）理解したと判定されることになります
問題はここからで，高校生活で獲得する機会の無かったであろう知識の獲得が多くなるのでご注意ください．
授業の内容についてその時間内で理解できるのは，概ね2/3以下のはずです（文部科学省の考え方　90分授業したら，授業外で180分（予習と復習）なので）既に上記の不明点について解決して理解しているだろうと期待しています
自身は授業中に理解できている事，理解できていないことも含め後で振り返れるように教科書等に書き込んでいました．それは授業の内容を自分で再現できるように記録することに注力していたように思います．
録音している学友もいたように思いますが，等時性メディアなので結局役に立ってなかっただろうと思っています．（授業よりも真剣に聞ける）

第05回　推測統計（２）区間推定(二項分布と正規分布)

【SO-02-03-03】正規分布の母平均の信頼区間について説明できる。
(教科書2章1,2,3　3章2標本平均の理論分布と標準誤差(SE)　7章)
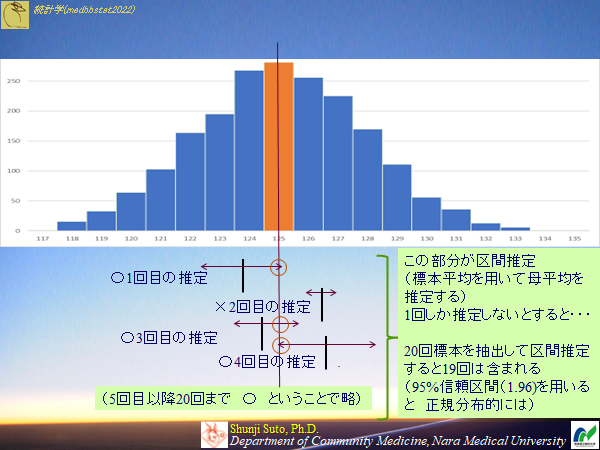
点推定の幅を持たせると，当たる（区間内に含まれる）確率は上がるが１００％では意味が無い
母集団の確率分布を知らない（もしくは推定できない）と区間推定は出来ない

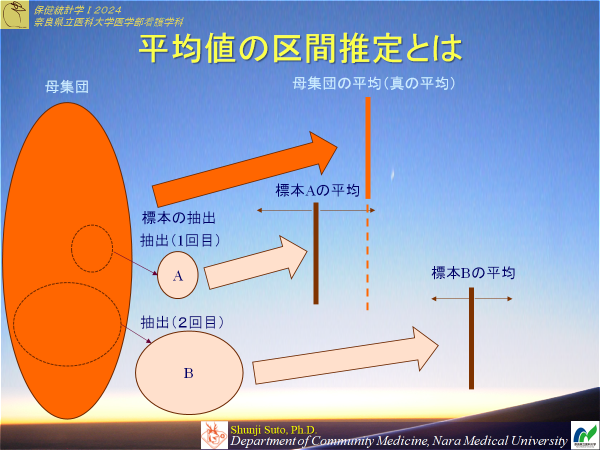
平均値の区間推定のイメージ

標準誤差

・標準偏差は標本の分布のバラツキ具合を示したもの
・標準誤差は母集団から抽出した標本の平均値のバラツキ具合
SE=σ／√n
ここでは，なぜ√nになるのか説明しないが，少なくともサンプルサイズが大きいほど標本平均のバラツキ具合が小さくなっていくことは理解できると思う
どうしても　という方は以下のリンクご覧ください．

＜参考＞標準誤差SEはなぜ標準偏差σを√nで除するのか（生物統計学2018奈良医大）
https://medbb.net/education/nmubiostat2018/index.html#SE

例題５－１

例題４－１の標本から標準誤差を求めよ

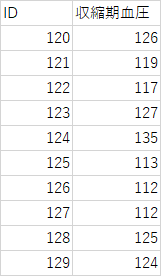
例題５－２

サンプルサイズ10000で求めた標本の平均が１１０，不偏分散が４００だった時の標準誤差を求めよ

サンプルサイズによる平均値の標準偏差＝標準誤差を導くことが出来た．
あとは確率の取り扱いだけ出来れば区間推定が可能

二項分布

ある事象が起こる確率が既知の時，試行回数に対して出現度数別の確率を求めたもの
出現度数ｒ=試行回数n×事象の起こる確率p
n回施行すると出現度数rは期待値になることが期待されるが，期待以外の度数になることもある（むしろ当たらない方が多いのでは？）
P_r＝_nC_r×p^r×(1-p)^n-r
P(r)=nCr*p^r*(1-p)^(n-r)

例題５－３

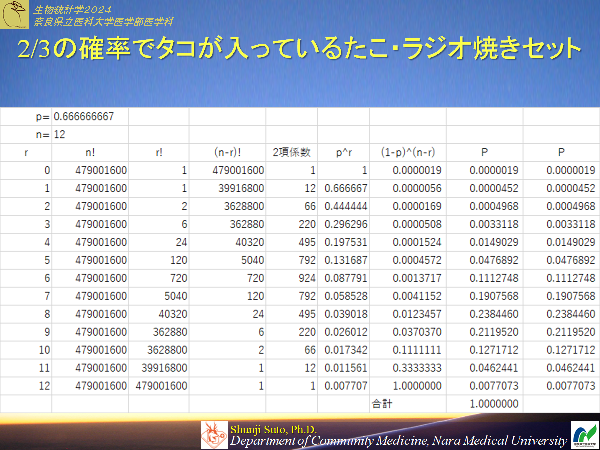
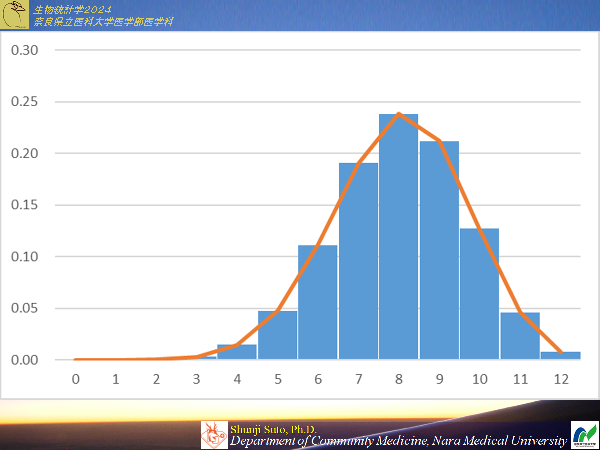
2/3の確率でタコが入っているたこ・ラジオ焼きセットがあったとする（タコの入手が困難なので不足を牛スジ肉で代用している）
12個入りのたこ・ラジオ焼きセットを買った場合たこ入りたこ焼きが10個以上になる確率を求めよ

＜参考＞ たこ焼きのはじまり（大阪たこ焼マーケット）
https://takoyakimarket.com/history.html

例題５－３では１０個以上（10,11,12個）の確率を累積したもので累積確率と呼ばれます．
ここでは離散量でnも小さいので，なぜ必要なのかイマイチ分かりにくいところですが連続量を取り扱うとすると・・・

例題５－４

例題５－３の計算結果を用いて期待値を中心に95%程度の確率が含まれる区間を求めよ

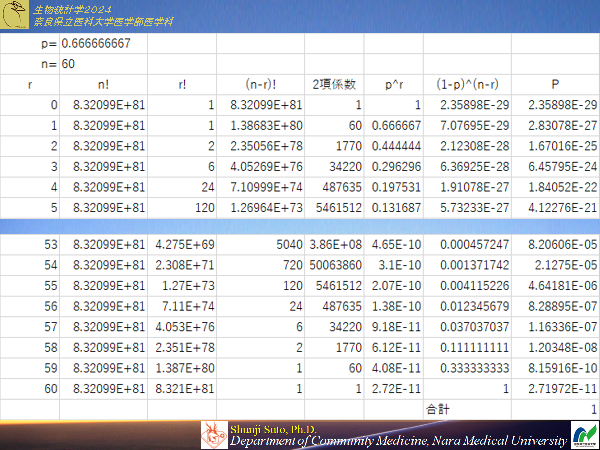
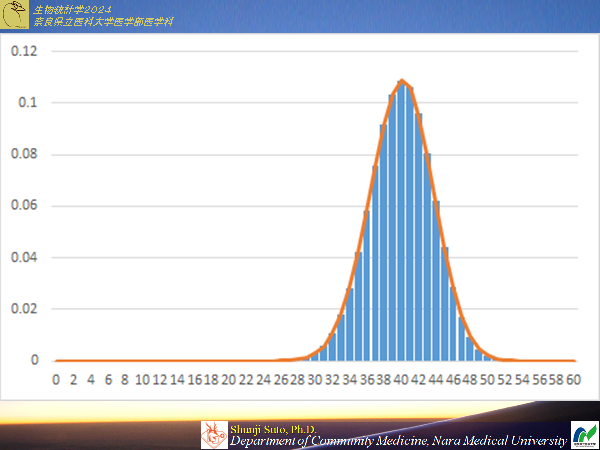
二項分布と正規分布（教科書P134）

二項分布のnが大きければ正規分布に近似する（μ=np　σ^2=np(1-p)）

正規分布

正規分布・・・偶然誤差の分布（＝精度の話）
区間推定では真度が高いものであることが前提となる
人体から取得するデータの分布は正規分布に近似なものが多い　→　教科書P35参照

＜参考＞
第7回 正規分布という王様が誕生する（統計の落とし穴と蜘蛛の糸　羊土社）
https://www.yodosha.co.jp/smart-lab-life/statics_pitfalls/statics_pitfalls07.html
正規曲線・正規分布の一指導法（水野 恭之,日本数学教育学会誌/66 巻 (1984) 7 号）
https://www.jstage.jst.go.jp/article/jjsme/66/7/66_24/_article/-char/ja/
14-1. 正規分布（統計WEB　株式会社 社会情報サービス）
https://bellcurve.jp/statistics/course/7797.html

中心極限定理

サンプル数が多ければ標本平均の分布は正規分布になる
　→正しく測定されているのであれば偶然誤差の発生は正規分布に従う
　→測定回数を増やせば増やすほど

標準正規分布

平均値が０標準偏差＝１（分散も１）になるように値を変換したもの
それをZ値という・・・標準正規分布表の行と列から求める値の事
偏差値は平均値を50、標準偏差＝１０になるように値を変換したもの
それを偏差値という

例題５－５

平均値が７５点の集団がある．標準偏差は５点．
そこで82点を取った人がいる．その時のZ値および偏差値を求めよ

標準正規分布表

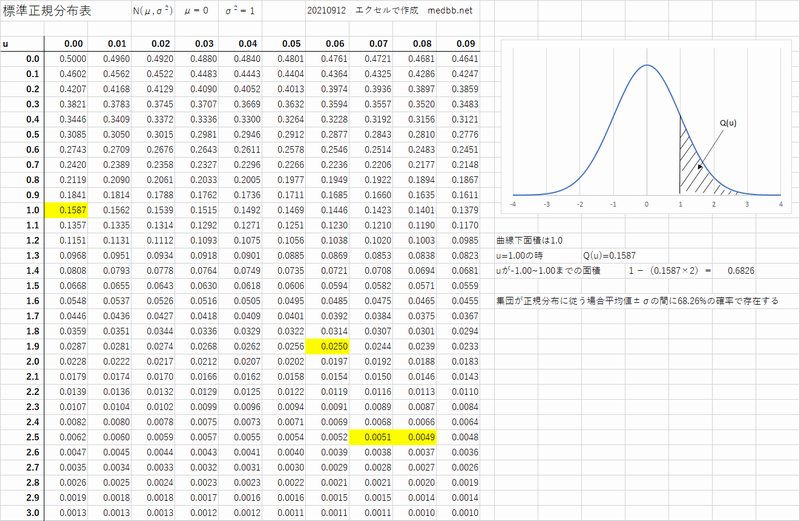
標準正規分布表のPDF版はコチラから

例題５－６

あるテストを受けたところ偏差値は６５と言われた．受験者が10000人とした場合，受験者の得点の分布が正規分布に従うとしたら，順位は？

例題５－７

あるテスト（受験者が10000人）を受けたところ85点だった．平均点は73点標準偏差は4点だった．受験者の得点の分布が正規分布に従うとしたら，順位は？

例題５－８

あるテスト（受験者が10000人）の平均点は73点標準偏差は3.5点だった．受験者の得点の分布が正規分布に従うとしたとき，平均点（73点）を中心に95%の人（9500人）が含まれる得点の範囲を示せ

標本を基に母集団の平均（母平均）を95%信頼区間で求める

ある試験の受験者１００人から点を教えてもらったところ平均値（点推定）＝６５点であった．なお母標準偏差は＝１８点であることがわかっている．
受験者全員（＝母集団）の平均値の区間推定を信頼区間95%で示せ

例題５－９

あるテストを受けた．受験者全員の平均点を推定したい．100名の受験者に協力してもらい点数を教えてもらった．
100名の受験者の平均点は80点，偏差平方和を求めたところ99000になった．95%信頼区間で受験者全員の平均を推定せよ

提出課題

本日の授業を受講したうえで，以下の2つの質問
１．理解できた内容，理解できなかった内容について
２．本日の授業の内容に関する質問（内容が概ね理解できているのであれば空欄でも可です）
を締切までに提出の事
締切は授業日翌日朝10時までとする

課題について

高校数学の範疇だけど実質？

結局入試対策によるところの範疇というところ
コアカリに明記されいるので，高校時代に取り扱っていない学生が多かったところからも丁寧に時間をとってよかったように思う

数学Bの教科書にあった　ｓｗも正規分布表の意味がわからず困惑していたが理解できた

高校では正規分布について全く習わなかった

Z値が難しかった

二項分布の計算や、標準正規分布については高校数学の知識もあったので理解しやすかった

二項分布については高校生のときにやらなかった

習ったことのある範囲

二項係数と確率の繋がりを思い出した

大学受験のために学んだ内容が少なかったため少し大変

共通テストで選択はしていない正規分布の意味が分かった

共通テスト数学IIBでも毎年3番だけど・・・

高校で統計をやっていなかったが理解できた

何故n-1？

n－1にする時としない時の違い、それによってデータがどう変わるか教えて頂きたい

第04回　推測統計（１）点推定(平均と分散)を一度読み返してください

数式について

95％、1.96の意味、偏差値の変換の仕方がわからないので解き方の式がほしい

式は覚えるものではなく理解していることで自然と導き出されるものなので
同じ部分を受講した（皆さんとは異なる）学生の感想
「答えは求められるが何故そうなるのかの理解が難しい．もう少し前の範囲からやり直す必要があると感じている．式を覚えるだけでは理解になっていないのでもう少し理解を深めたい」
「偏差値の求め方を式で覚えるのではなく考えて理解することができた。Z値が先に出てくるということも理解することができてすっきり」

概念問題

推定の統計と正確であるとした統計のどちらのことなのか

推定の統計・・・・推測統計（母集団（対象とする集団）全てを把握できないので一部から推測）
正確であるとした推定・・・正確であるとした統計・・・母集団（対象とする集団）全てを把握している場合の記述統計

第06回　推測統計（３）平均値の区間推定(t分布)，検定の考え方

【SO-02-03-03】正規分布の母平均の信頼区間について説明できる。
(教科書4章1正規分布とt分布の違い,2) 【SO-02-03-04】相関分析、平均値と割合の検定等を実施できる。
(教科書4章1,5章1,教科書3章1)

t分布による区間推定

母集団の平均値を推定するにおいて，標準正規分布を使うと上手くいかないケースがある・・・特に標本数が少ないと
困っていたゴセットさんが標本数によって平均値の出現する確率が変化する分布を示しました．
諸々の理由でt分布と呼ばれています．

＜参考＞ 酒井 弘憲，ギネスビールと統計家ペンネーム　スチューデント，ファルマシア51巻12号,2015
https://www.jstage.jst.go.jp/article/faruawpsj/51/12/51_1168/_article/-char/ja

t分布

t分布は標準正規分布と同様に，標本より求めた母標準偏差の推定値（不偏分散に基づく標準偏差）を用いるが，標本の自由度（サンプルサイズより求める）によって変化する．
サンプルサイズが大きくなるとｔ分布は正規分布に近似されていく．

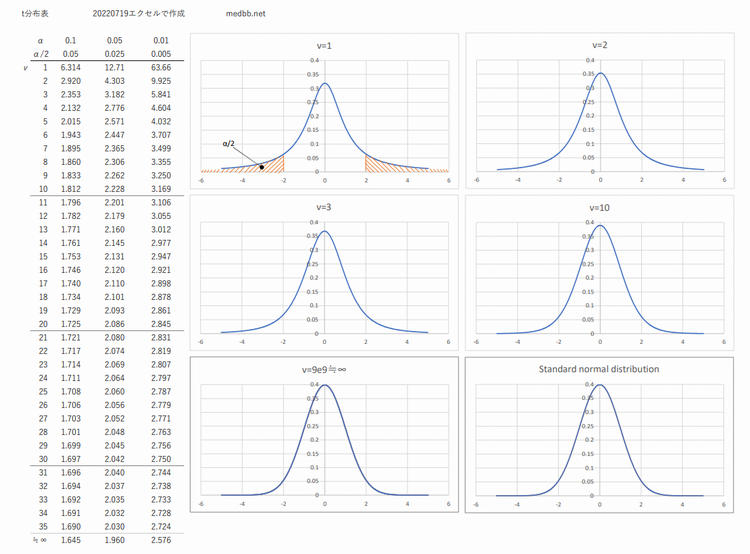
t分布のPDF版はコチラから

「自由度」νが出てきますが，以下考え方

標本の中で自由に振る舞うことが許されている値の数
例えば標本から平均を求めたとき,その平均が母数の推定値としたら、自由に振る舞えない値が出てくる（つじつま合わせ）
t分布は抽出した標本数を基にしたものなので，正規分布のように一義的なものでは無く，標本数（自由度）によって確率分布が変わる

例題６－１

10円玉の重さを知ろうと思い立ち，手元にある10円玉10枚を測定したところ以下のようになった
10円玉の母平均（期待値）を95%信頼区間で区間推定せよ
どの確率分布を使ったらよいのか，皆さん知っているはずですがあえて，正規分布を用いた場合，t分布を用いた場合双方で実施し，その違いについて検討せよ
有効桁数はそれぞれ3桁で計算してください

10円玉ID	重量(g)
1	4.55
2	4.53
3	4.23
4	4.50
5	4.51
6	4.31
7	4.38
8	4.54
9	4.35
10	4.30

＜参考＞ 自販機 （秘）お札が戻る訳（知識の宝庫！目がテン！ライブラリー）
https://www.ntv.co.jp/megaten/archive/library/date/08/03/0316.html

例題６－２　自由度が∞の時のt分布の95%信頼区間は正規分布と同じであるが自由度νが13の時，正規分布の何パーセント信頼区間に相当するのか？

仮説検定

仮説検定はなぜ必要なのだろうか？

仮説検定はなぜ必要なのだろうか　と　chatGPT3.5に聞いてみた

頼れる存在ですが，余計なことも話さないと気が済まないようで，手順まで答えてくれました．最後のまとめ部分が以下「」内です．文がこなれていないので取り様による部分があったりしますね
公式の件と同じですが，理解したことを自分の言葉で文章に起こすことが重要で，これ丸暗記したところで説明できなければ学修したと見做せませんよね．
「仮説検定は、データからの結論の信頼性を判断し、科学的かつ客観的な方法で結果を導くために不可欠です。これにより、様々な分野での意思決定や研究の信頼性が向上します。」

検定（有意差検定）と推定の違い

推定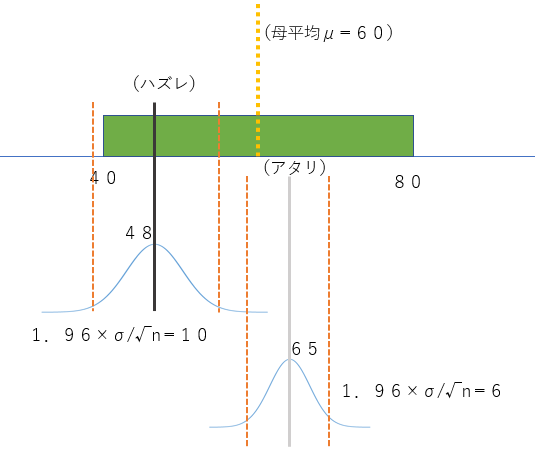

検定

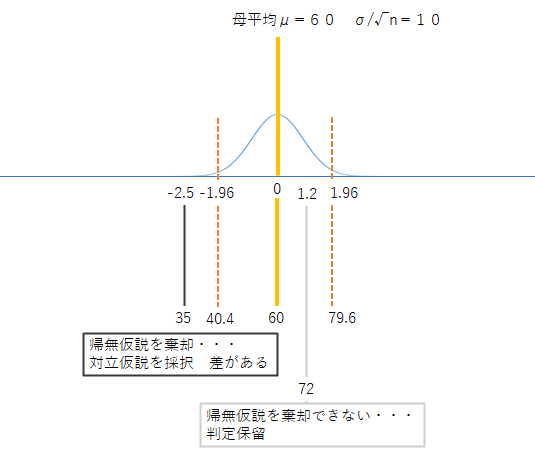
科学と統計

初回の講義をを思い出していただいたら良いかなと思いますが，以下抜粋
小学校学習指導要領（平成 29 年告示）解説　理科編（文部科学省）より

科学が，それ以外の文化と区別される基本的な条件としては，実証性，再現性，客観性などが考えられる。
実証性とは，考えられた仮説が観察，実験などによって検討することができるという条件である。
再現性とは，仮説を観察，実験などを通して実証するとき，人や時間や場所を変えて複数回行っても同一の実験条件下では，同一の結果が得られるという条件である。
客観性とは，実証性や再現性という条件を満足することにより，多くの人々によって承認され，公認されるという条件である。

実証性

「考えられた仮説」が無いことには始まらない→仮説検証型
それでは「考えられていない仮説」とは？
→まだ十分に確固たる仮説として成立していない仮説

仮説検証型と仮説探索型

仮説探索型とは「考えられた仮説」が存在せず（関心ある事象など），得られた結果は「考えられた仮説」になる可能性を有するので「まだ考えられたと言い切れない仮説」

再現性

仮説を実証するために得られたデータから複数回，同一の検証結果になること
「常に」同一の検証結果になることを求めていないが，それは求められないから

再現性の限界

再現性の条件は「仮説の実証を複数回行っても同一の結果が得られる」ことですが，その回数が無限であるならばその条件は永遠に満たされません．
故に有限となりますが，それはある回数（x回）まで同一の結果としても，x+1回目以降同一の結果にならない可能性を含んだものになります．
これは未来において，その仮説が覆される可能性があることを示すもので，反証可能性といわれるものです．

再現性の限界を超える方法

「仮説の実証を∞回行っても同一の結果が得られる」
実証で得られたデータについてどのようなものであっても同一な結果が出るように判定基準を定める

例題６－３　再現性の限界を超える（つまり同一の結果が100%出るような判定基準を定める）ことがよろしくない理由を考えよ

判定基準

「同一の結果」が100%の確率で出現しないことを示しておく必要が出てきます 例えば仮説の実証を行うにあたって検証データに対する判定基準を目標値（目標とする効果量）として設定した場合，達成してもその判定基準が「『同一の結果』が100%の確率で出現しない」ものか分かりません．
例えばその目標値が医学的に妥当なものであったとしても，ここでは関係ない話になります
そうなると，確率に基づく基準で判定しないことには，再現性を満たすことが出来ません
故に仮説検定では効果量などで判定せずに確率に基づいて行います

統計的有意差と臨床的有意差

得られたデータに基づき計算した確率が判定基準を下回った時に統計的有意差があると言います．
知見は社会実装することで人類に貢献できますが，医療現場においては臨床的に意味があるとされる量を基準とする臨床的有意差が結果として求められます
無論社会で役立てていく知見としては，統計的有意差よりも臨床的有意差が重要になりますが，「科学的」な観点からは前者が支配的になります．
確率の違いを量で示すとき，その量はサンプルサイズにより変化します．故に臨床的有意差に基づきサンプルサイズを決定することで二つの違いを解消できます
例えば臨床的有意差が統計的有意差よりも大きい場合は再現性については確認できたものの臨床的な観点から確認はできません．統計科学的に良いが，医科学的には？という結果になります
一般にはサンプルサイズが大きいほど，精度の高い結果が得られるので良いという感覚に思いますが，それは区間推定の話で仮説検定において効果量の差を検証する場合は少し状況が異なります

提出課題

本日の授業を受講したうえで，以下の2つの質問
１．理解できた内容，理解できなかった内容について
２．本日の授業の内容に関する質問（内容が概ね理解できているのであれば空欄でも可です）
を締切までに提出の事
締切は授業日翌日朝10時までとする

課題について

残念ながら全員が丁寧に復習しているとは思えない状況になってきたようです

うーん　わかってないんだろうな　解決できないのであればご連絡ください

n-1で割ることの意味をt分布から理解

なぜ偏差平方和を自由度で除すると母分散の不偏推定量になるのでしょう？私そんな説明してないけどなぁ　皆に説明していただけるとありがたい

未だに例題6-1でなんでしたに√9も√10もかけるのかわからない

第4回～5回の部分が理解されていない感じですね

区間推定の求め方が理解できない

第5回の部分が理解されていない感じですね

科学は完全に再現することはできないので、再現性は求められていないということが分かった

科学でなければそれで構いませんが，科学であるとするならば当然求められます．ただし科学でも「永遠の再現性」は求めておりませんが

t統計量の定義 t = (X - m)/SE が授業で示されなかったので，だから自分で探した

まず，t分布の経緯を説明し正規分布の代替として説明したので，推定で特に必要無かったかと思います．
予習されていて検定の話で出てくるからと先読みされていたように思いますが，予習として他の学生の模範となる好ましいことです．
定義の提示だけの話に見えましたが，既に意味合いも理解もされているのだろうと思います．ですので以下は受講生皆さんに向けてですが

私は，Z（標準正規分布）と同じようにt（t分布）も同じように求めるだけという話で進める予定ですので，改めて「定義」として示すものでも無いかなと思っています．
推測統計の時に用いていたZやtを逆算して求めているだけなので．故に示したいただいた定義について学生に丸暗記してほしくないので強調するつもりもありません．（教科書に書いてありますが，理解の確認のために書いているだけという位置付けです）
式を最初に丸暗記するのは個人の自由なので否定しませんが，理解のキッカケを奪いかねません．チャンスを利用しスムーズな理解を目指して授業を進めているつもりなのでその点ご理解ください
（過去に偏差値の話とZ値の話と偏差値とZ値の関係についてをそれぞれ示してからZ値を求める問題を出したら，なぜか偏差値を求めて関係式を用いてZ値を求めた学生がいてショックを受けたので）

質問系

「1.96の意味とは？」という質問は、「なぜ95%で推定するのか？」という質問と同値で、無意味な質問であるという理解

それで良いです．

再現性が100％だとよろしくないのがよくわからなかった．高すぎるといけなかったらどのくらいがいいの？

再現性１００％を要求されると人類が続く限り永遠に満たせないから．仮説検定は95%の確率が一般的
この件書いていたら脳内で流れてきた曲は以下
この曲（ドラマ）が医療職を志すキッカケになった方もおられるかと思いますが，科学の条件である再現性の話を意識してご覧ください

t分布を用いる場合、標本のサイズに応じて式の中で用いる数値が異なってくる？

その通りです

来週に持ち込み部分（一気に進んだほうが良かったですよね）

仮設検定の実用例がわからない　検定の話もなんとなくしか分からなかった。

知識を有していることで新たな知識を理解しやすくなる

今回も大学受験の時に学んだ知識があまり活かせない内容だったのでかなり大変

高等教育のスタートラインですね．90分の授業に対して180分の予習復習です

第07回　推測統計（４）パラメトリック検定

(教科書4章1,5章1,教科書8章1,3,10章1Q7) 【SO-02-03-04】相関分析、平均値と割合の検定等を実施できる。

パラメトリックとノンパラメトリック

教科書P44

分布の形状（母数）に依存する統計量（平均値　標準偏差・・・量的変量）
分布の形状（母数）に依存しない統計量（順位　中央値　パーセント値・・・質的変量）

教科書P4-7,204

パラメトリック検定・・・計測値の分布が何かしらの確率分布であることを仮定
正規分布であるかどうかを確認・・・正規確率紙法・・・ここではQ-Qプロットの話で進めます（縦軸（期待値）　横軸（実際の値））
データをノンパラメトリックとみなして順序に直してそこからパーセンタイルを求めて、値を確率分布（正規分布）に代入して期待値を算出して比較する。
P11複雑な調査データTGを用いて

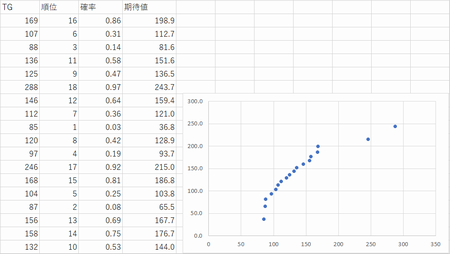
＜参考＞Excelによる正規確率プロットの作り方（統計WEB　SSRI）
https://bellcurve.jp/statistics/blog/15362.html

仮説

仮説検定では確率に基づく判断基準を有意水準として確率で示します．
以降は「新たな知見」に対する話で仮説検定を用いるケースが重要なので有意差検定を前提として話を勧めます
事象としては「同一の結果が得られる」「同一の結果が得られない」の二つにいずれかになります．
同一の結果が得られる仮説を帰無仮説（これまでと違いが無い仮説）H0，同一の結果が得られない仮説を対立仮説（これまでと違いがある仮説）H1と示します．有意水準は対立仮説H1の確率を示します
有意水準は通例5%とされることが多く，両側検定（効果量に違いがあるのか無いか）と片側検定（違いがが正の方向のものなのか，負の方向のものなのか）の二種類があります

差がある仮説の判定（有意差検定）

研究活動は「新たな知見」を見出すことを目的にしてますので，通常この検定になります．
区間推定を思い描いていただいたら，概ね同様な話ですが表現の仕方が帰無仮説／対立仮説の二値化されることと，区間推定と違い帰無仮説に基づく話（例えば差が0としているならばその値が中心，区間推定の場合は標本から求めた平均が中心）になる違いがある程度です．
帰無仮説そのものは「考えられた仮説」ではないので採択された場合の判定は保留になります
帰無仮説が棄却された場合残された仮説は対立仮説のみとなります．こちらは「考えられた仮説」になります
背理法の考え方に基づく論理になりますが，もともと証明したい仮説（差がある）を偽であるとして，矛盾を導く出すことで判定する方法になります
現在はコンピュータにより確率を直接求めることは可能ですし，まどろっこしい流れに映りますが，違い（差）を直接判断しているのではなく「同一の結果が得られる」確率に基づき判定基準を定めているところが科学として重要であるから故と捉えています．
ですので確率そのものは，判定のためのものであって求めた値（統計量や確率）そのものに重きを置く必要はありません．効果量そのものに重きをおく方が知見の社会実装の観点から重要になります

仮説検定（有意差検定　両側検定）のフォーマット例

手順１　帰無仮説，対立仮説をたてる

帰無仮説Ｈ_０：μ＝１５０　対立仮説Ｈ_１：μ≠１５０

手順２　母集団が従うと見做す確率分布を定め，有意水準を決める

（例えば）正規分布に従うと見做し，有意水準両側5%とする

手順３　今回取得したデータをもとに，母集団が従うと見做す確率分布における統計量を求める

（以下はケースX）
ここではよろしくないの承知で，正規分布としました
取得したデータの平均値（標本の平均）と帰無仮説に基づく母集団の平均値（母平均）の差を，確率分布（標準正規分布）における差に変換する
帰無仮説H0がある集団の収縮期血圧μ＝150mmhgとしたときに，得られたデータ（サンプルサイズn=36　標本平均xbar=147.3　不偏分散s^2=81）で検定を行う
考え方は区間推定と同じように現実の世界と確率分布の世界を行き来できるようにすること
（5回目の授業に示した図）

検定統計量は現実の世界における標本平均と帰無仮説で定めた値の差分xbar-μ，これが標準正規分布の世界でどのような統計量（z）になるのか
１）標準正規分布の世界はμ＝０　現実社会でのμ＝１５０　標本平均のμからのズレは１４７．３－１５０＝－２．７となる
２）－2.7は現実社会（サンプルサイズn=36　標本平均xbar=147.3　不偏分散s^2=81）によるものなのでσ(ここでサンプルは標本平均を求めているので標本平均の標準偏差，すなわち標準誤差SE=√81／√36=1.5の世界　これを　標準正規分布の世界(σ=1)に合わせると　-2.7/1.5=-1.8

手順４

検定統計量を用いて有意水準との比較，今回の標本が棄却域にあるのか否か（受容域なのか）判定する．
１）（ケースX） ｜ｚ｜＝1.8　p=0.0359×2（両側検定なので2倍）＞0.05
帰無仮説を棄却できないので判定を保留する
２）（ケース１）有意水準よりも小さい場合 ｜ｚ｜＝2.96　p=0.015×2（両側検定なので2倍）＜0.05
帰無仮説を棄却し対立仮説を採択する　有意差がある
３）（ケース２）有意水準よりも大きい場合 ｜ｚ｜＝1.45　p=0.0735×2（両側検定なので2倍）＞0.05
帰無仮説を棄却できないので判定を保留する

注）標準正規分布表の場合確率まで求めることが可能だが，t分布表は統計量から確率を求めることはできないので統計量で比較する

例題７－１　有意差検定において背理法を使わなければならない理由を考えよ（何故，違いがあるという仮説を直接証明しないのか？）

1標本(1群)t検定

世の中（母集団）の基準値など，既に明らかになっている事柄と比較することで世の中の一般的な状況と対象とする集団が異なっていることを明らかにすることを目的

例題７－２

物騒な話ですが，ある自動販売機に偽造通貨が使われているのではないかという話が私のところに舞い込んできた．
話を聞くともっともらしい仮説が既にあるので検証することにした．
そこで，自販機に入っていた硬貨１０円玉１０枚を用いてこの仮説について仮説検定を行う
10円玉の硬貨μ＝4.50gと比較して異なることが期待される検定になります
ここでは，とりあえず標準正規分布で検定してみましょう（よくないけど）
計算した結果ですが
標本の平均は4.42g
不偏分散より求めた標準偏差は0.119
をお使いください．

10円玉ID	重量(g)
1	4.55
2	4.53
3	4.23
4	4.50
5	4.51
6	4.31
7	4.38
8	4.54
9	4.35
10	4.30

例題７－３

例題７－２の結果を先方にお伝えしたところ，適切な統計手法を用いていないとご指摘を受けました．
そこで改めてt分布を用いて検定を行ってください

検定で注意する点

両側検定と片側検定の注意点

教科書P207
一緒な有意水準で比較した場合　片側は棄却域が存在しないことと，他方は棄却域が大きくなってしまう　→　帰無仮説が棄却されやすくなる状況

有意水準は常に0.05？

教科書P208
有意差は有意水準が一緒でもn=が大きくなると少ない差でも優位と判定されてしまう．
統計的有意差≠臨床的有意差
効果量を目的としているわけで，統計的な差（違い）が現実社会の中において意味がある差なのか

各群サンプルサイズ10の場合で検定すると10kg程度となるが、そこまで体重が変化しているとなにか違う出来事が起こっている気がする
各群サンプルサイズ1000の場合検定すると1kg程度で有意な結果となるが、本当に意味あるのか気になる
　
　

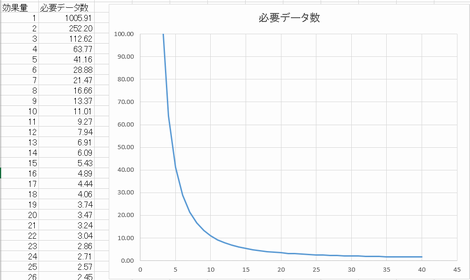
αエラー　βエラー

教科書P215

第一種の過誤

（αエラー）・・・誤って差があると判定する確率
αエラーの起こる確率（誤って有意差があると判定）＝有意水準
エラーを気にしなければいつの日か、都合の良い結論が得られるかもしれない　→　雨乞い
故にやみくもに検定するのではなく、至るまでのストーリーが大切

第二種の過誤

（βエラー）・・・誤って差が無いと判定（＝判定保留）する確率
βエラーの起こる確率（誤って有意差が無いと判定）＝検出できない＝１－検出力（Power）＝β
検出力＝１－β
サンプル数↑・・・検出力↑・・・β↓
一般に検出力0.8～0.9で違いを見積もった上でサンプル数を決定する
検出力をが上がるとβエラーの確率は下がるが，統計的有意差と臨床的有意差の話が出てくる．

統計的有意性とp値に関するASA声明

＜参考＞統計的有意性とP値に関するASA声明（日本計量生物学会）
http://biometrics.gr.jp/news/all/ASA.pdf
以下の内容が指摘されています
1. p値はデータと特定の統計モデルが矛盾する程度をしめす指標のひとつ
2. p値は、調べている仮説が正しい確率を測るものではない
3. 科学的な結論は、p値がある値を超えたかどうかにのみ基づくべきではない
4. 適正な推測のためには、すべてを報告する透明性が必要
5. p値は、効果の大きさや結果の重要性を意味しない
6. p値は、それだけでは仮説に関するエビデンスのよい指標とはならない

例題７－３　特に小標本の場合仮説検定においてt分布（t検定）ではなく標準正規分布を用いた検定（Z検定）を行ってしまうとどのような困ったこと（結果だけ見ると喜ばしいのかもしれないが）が起きるか

提出課題

本日の授業を受講したうえで，以下の2つの質問
１．理解できた内容，理解できなかった内容について
２．本日の授業の内容に関する質問（内容が概ね理解できているのであれば空欄でも可です）
を締切までに提出の事
締切は授業日翌日朝10時までとする

課題について

理解に差が出てきてるかなと思います

理解は突然訪れる

この経験が重要で，この経験を様々な領域でしていただくことが理解力の向上に繋がります

有意差検定の標準誤差のつながりが初めは見えずらかったが、突然理解

やっと区間推定95パーセントの意味が分かりました

統計的有意差と臨床的有意差の違いがやっと

安易に暗記に頼らない学生に感謝

その地道な取り組みが将来役に立つことと思います
皆さんは，まだ誰もが辿り着いていない事柄と向き合い解決することを特に条件が限られた中で進めなくてはならない立場になるので

公式の根拠を理解することができた

第4回あたりからあまり理解出来てないことがわかり

今回も高校で習った範囲とずれていて難しい

今までと逆の操作をしていることに気づく

仰る通り

正規分布を使った検定は、t検定より対立仮説が採択されやすい

故にt検定を使った鵜が良いケースが多くなるのも当然かと→実質αエラーが出やすくな格好に繋がる

これまでの内容の総まとめ的な感触だった

片側検定

片側検定というものの存在意義が分からない

t検定においては，基本両側検定で行っているからどうしてもそのまま片側だと棄却域が片方だけに拡がるところが見えてるだけにですよね
ちなみにカイ二乗検定では上側だけで検定することになりますが（片側っぽくみえますよね）そのようなものもあります

妻の病気が治らない人の話を聞いて、やっと腑に落ちた感じ

このエピソードは夫婦愛に基づくものと捉えています

気をつけなければ間違いを突き進めることに繋がる

そのような理解をされていれば，片側検定の論文読むとき，色々なところに関心が出てくるようにも思います

その他未整理

高校で帰無仮説を発展として習ったがあまりよく分かっていない
正規分布を使った検定は、t分布を使った検定に比べて対立仮説が採択されやすい
t分布と正規分布のどちらを使うか意識しないと全部正規分布をつかってしまう
どうして差を標準誤差で割るのかがわからない
標準誤差で割っているのは、標本平均が真の平均からどれだけ離れているかを考えるためという認識で大丈夫
例題7-2のp値ってなんですか？
t分布と標準正規分布の使い分けが難しい
テスト形式を知りたかった
標準誤差を平均値とのズレで割る理由がわからない
復習してても、理解が遅いので授業内でついていけず、結局うやむやのまま授業を受けてまた復習となるので、復習の質も悪い
論文や研究者の講義を聞いている中で、P値がでてきて、有意差があるとかなんとか言っていたが、その意味がやっと今回の講義で理解
仮説検定のやり方の例の手順3で標準誤差で割っているのは、標本平均が真の平均からどれだけ離れているかを考えるため
検定できない。まずい
t分布が難しい
公式丸暗記ではなくなぜその式になるかの理解に努めたい
仮説とは、例えば「私の投与した薬の効果はある」
t分布と正規分布のどちらを使うか意識しないと全部正規分布

第08回　推測統計（５）ノンパラメトリック検定（パラメトリック検定積み残しも）

(教科書4章3,5章4,8章3)

1標本(関連2群)t検定

paired-t検定とよばれます．
前後（ビフォーアフター）に違いが見られたかどうかを検証するものになります．
同一の対象者それぞれの介入前後に差が見られる（つまり介入による影響がある）仮説を検証するものです
1標本t検定(1群)において基準値が0（＝違いが無い）が帰無仮説となります

paired-t検定は１標本，２標本？

paired-tは結果として実施していることは一つの標本（差分）についてなのか否かの検定を行う格好なので，行っていることは一標本(関連した2群の)t検定になるのですが，標本数に触れずに独立した形で説明しているケースもあります
「標本」が何を示しているかの話ですがあくまでも対象の話（複数のデータを取得することは可能）なので用いた標本は一つという所だと思います．
無論介入前後の状態であったとしても，ペアになっていない標本を抽出したならば当然ですが二標本(独立した2群の)t検定となります

例題７－４

リハビリ前後の患者さんの動作にかかる時間（秒）を測定したところ以下の結果になった．
この介入において動作にかかる時間の変化より効果があったのか検定せよ

被験者ID	介入前動作（秒）	介入後動作（秒）
1	16	9
2	19	16
3	13	11
4	20	16
5	23	18
6	15	10
7	19	13
8	12	17
9	15	14
10	18	16

2標本(独立2群)t検定

教科書P6テーブル（適用要件による使い分け）

1標本t検定・・・空白
2標本t検定・・・２群の等分散性
空白の意味は、データの元（標本）が同じなので問題が生じない
２群の等分散性に関しては、ぞれを前提として検定が成り立っているので（以下に紹介する（スチューデントの）t検定は
無論、等分散ではない場合に用いる検定（ウェルチのt検定）もあるのですが、そちらを最初から使った方が良いという話があります。
ノンパラかパラメトリックの話と同様ですが、どちらでやろうとも明確な有意差が結果として見られるものが理想ではありますが

例題７－５

リハビリ介入群と非介入群のそれぞれの動作にかかる時間を測定した．
測定結果は以下のとおりである．
この介入に効果があったのか検定せよ
なお，介入群の不偏分散は11.6　非介入群は9.78　として計算せよ

被験者ID	介入有群	介入無群
1	16	9
2	19	16
3	13	11
4	20	16
5	23	18
6	15	10
7	19	13
8	12	17
9	15	14
10	18	16

一標本Wilcoxon検定

ウィルコクソンの符号付順位和検定
教科書（P6)・・・分布型，計測尺度，分散の制約なし
教科書（P74）
１：ペアのデータの差dを求める
２：dの絶対値よりそれぞれの差（d）の順位（昇順）を求める
　　同順位の話・・・教科書P76参照
３：検定統計量Tは＋，－別に順位を足したもので小さい方
T₀=min(T₁,T₂)
有意確率については直接計算出来るが（P75）延々と計算していくのは大変
n≦25まではWilcoxon検定表が用意されています（P274)
N数が少ないと（空白の部分）判定保留にしかならない
教科書P78参照のこと

n＞25は正規分布に近似と見なしてz値を求める方法で検定

平均値

μT=n(n+1)/4

標準誤差

σT=√(n(n+1)(2n+1)/24)

検定統計量

Z=(T-μT)/σT

連続補正

P137参照

P76(例題10)で説明します．

提出課題

本日の授業を受講したうえで，以下の2つの質問
１．理解できた内容，理解できなかった内容について
２．本日の授業の内容に関する質問（内容が概ね理解できているのであれば空欄でも可です）
を締切までに提出の事
締切は授業日翌日朝10時までとする

課題について

いまさら私に言われても

学生証が反応しない云々とありましたが，授業時間内（最初の時点）で私に相談されていないので対応困難です．教育支援課にその旨お伝えください

所感

概ね順調ですが，ウィルコクソンが若干時間が足りなかったのかなというところです
二標本t検定は計算がややこしくなる部分で，困っている方がいたが単純に合成しているだけと思ってみるとそこまでややこしくないのでは？

第09回　中間まとめ（小テスト）

（小テスト　今年度は07回目までの内容で実施）

第10回　推測統計（６）度数に関する検定（ノンパラメトリック検定積み残しも）

【SO-02-03-04】相関分析、平均値と割合の検定等を実施できる。

Mann-Whitney検定

二標本になるとややこしくなるのはパラメトリック検定と同じ
P102-113参照
検定統計量
自群の個々について、それよりも他群で大きい個体数の総和を求めて検定統計量としている
１：ある群（A）の値それぞれがもう一方の群（B）に入ったとしたときに（Aの）その値よりも（Bの群のなかで）値が大きい個数をカウントする。（A群の）全てについて行い和をとる。（順位-1の話）
２：AとBを入れ替えて１：と同様の計算をするか、公式でB群の和を求め小さい方を検定統計量Uとする
　　同順位の話・・・教科書P103参照

こちらも標本数が多くなると正規分布の話が出てくる

平均値

μU=n₁n₂/2

標準誤差

σU=√n₁n₂(n₁+n₂+1)/12)

検定統計量

Z=(U-μU)/σU

P104(例題17）P110(例題19)で説明します．

例題８－１

例題７－４　例題７－５について，それぞれノンパラメトリック検定を行ってください

計量値と計数値

計量値・・・量を測定
計数値・・・頻度を測定（名義尺度）
量的変量は頻度の測定も出来る．（連続量から変換する必要があるけど）
どのようなデータにも使えるので，色々なところで出てくる

カイ二乗分布

教科書P142
χ２乗分布・・・母分散を推定できる確率分布
χ^２＝ΣＺ_ｉ^２
平均からのズレの平方をとったものを足し合わせていく→偏差平方和
標準正規分布に従う独立した確率変数が1つの場合
χ^２＝Ｚ_１^２
＜参考＞独立した確率変数が二つの場合
χ^２＝Ｚ_１^２+Ｚ_２^２

カイ二乗分布表（教科書P273）

t分布と同じく自由度により確率分布は変化する
カイ二乗分布（ν＝１）の時のそれぞれの上側確率に相当する正規分布の確率（両側5%（片側2.5%ずつ）は全て上側に集約されてしまう

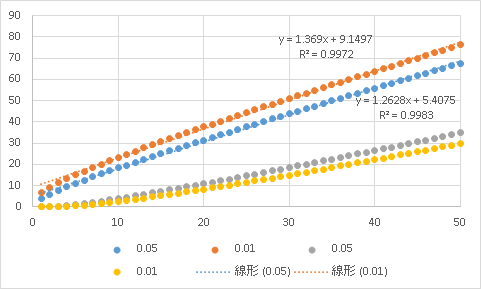
χ^２=（（X-μ）／σ）^２
χ^２_０．０５=（（１．９６-０）／１）^２
例）標準正規分布で有意水準両側５％の場合の境界値はz=1.96．カイ二乗分布表より優位水準上側５％の時のカイ二乗値＝3.84

ピアソンのカイ二乗

カイ二乗分布の話（X-μ）を（実際に出現した度数－出現が期待される度数（期待値））に置き換え
分散で除することで分子の差分を標準正規分布のN(0,1)にしていたものを，期待値で除して求めたものである．
(ポアソン分布であるとすると平均値＝期待値＝分散)
カイ二乗値＝Σ（観察度数－期待値）^２／期待値

検定

適合度の検定

P140例題28で説明
1行ｎ列
事象の起こる確率に基づく頻度（＝n×ｐ）期待値（度数））と実際に観測された度数（観察度数）の差異について検定．帰無仮説（測定した分布は想定されている分布と等しい）Ｈ_０：Ｐ＝（1/6,1/6,1/6,1/6,1/6,1/6)・・・サイコロの場合

独立性の検定

ｍ行ｎ列
こちらはそれぞれが独立しているか（関係があるか無いか）を検定
考え方は一緒
事象の起こる確率は実際に観測された度数を基に算出して全体の度数を乗じることで期待値（度数）とする．

Fisherの直接確率法

期待値が低い場合、．wilcoxonの統計量T理論分布と同様だが計算大変
故に教科書では２×２表以外出てこない（考え方は一緒）
例えばP146例題より直接確率を求めたものが以下

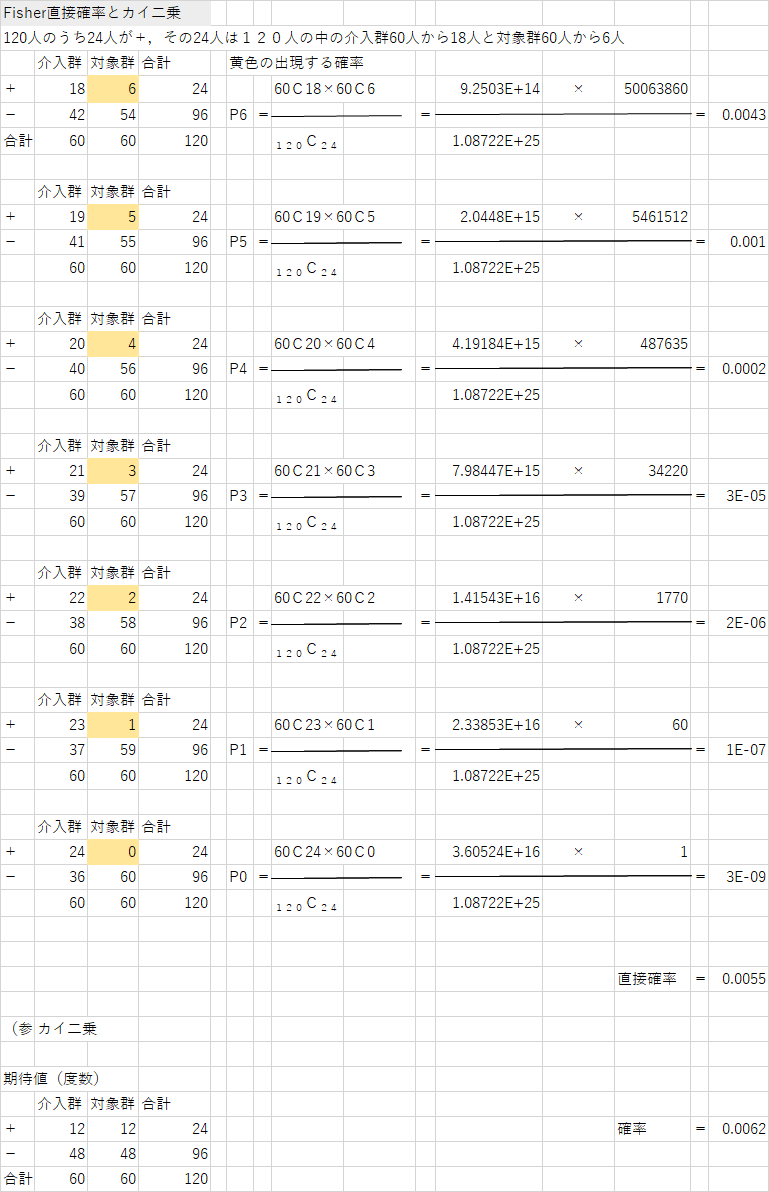
例題８－２

以下のサイコロについて通常のサイコロと異なる可能性である可能性が高いので検定を行った

サイコロ	１	２	３	４	５	６
観察度数	8	7	4	10	14	11

統計量カイ二乗値＝6.67

例題８－３

以下の薬剤と尿糖の関係について検定を行ってください

観察度数	薬剤A	薬剤B	薬剤C
尿糖＋	14	22	44
尿糖－	28	40	52

統計量カイ二乗値＝2.67

提出課題

本日の授業を受講したうえで，以下の2つの質問
１．理解できた内容，理解できなかった内容について
２．本日の授業の内容に関する質問（内容が概ね理解できているのであれば空欄でも可です）
を締切までに提出の事
締切は授業日翌日朝10時までとする

第11回　相対リスク（の前に多重検定のお話も）

【GE-01-04-02】PICO（PECO）を用いた問題の定式化かができる。
【SO-02-02-02】割合・比・率の違い及び代表的な疫学指標（有病割合、リスク比、罹患率等）を理解している。
この授業では相対リスク=Relative Risk は一般的な用語であり、その算出指標の一つにリスク比（Risk Ratio）があるのですがそれを相対危険としているケースもあり，言葉の整理が出来ていないところでもあります。

検定の話はここまでになります．

多重検定

教科書P217
ポイントとしては、それぞれの検定が独立した仮説にもとづいたものと考えて良いか否か。良いのであれば多重検定にならない
一連のものであれば対立仮説を考えたときに有意水準が５％と言いながら５％になっていないのでは？
多重に検定することでどれかあたれば帰無仮説は棄却できるので例えば3群総当たりだと有意水準0.05で多重検定（6通り）すると有意水準が0.265になってしまう。（からよくない）

有意確率補正法

Bonferriniの場合は6通り検定するのであれば、一検定あたりの有意水準だと0.05/6=0.0083となる。全体では1-(1-0.00833)^6=1-0.95103=0.0490
Sidak補正の場合は同様に1-(1-0.05)^(1/6)=0.008512　1-(1-0.008512)^6=1-0.95=0.0500
多群になるほど検定あたりの有意水準が下がる→差が出にくい

多重比較法

パラメトリック法
Tukey法・・・各ペアに対する平均値の差の検定
Dunnett検定・・・一つの対象群との対比

ノンパラメトリック法
Dunn法

問１１－１

曜日別に検査の管理用資料を測定した。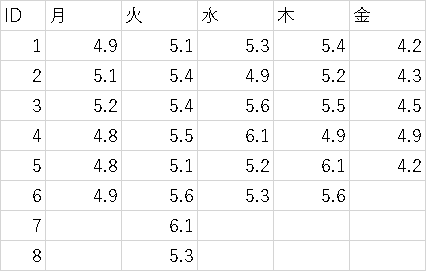


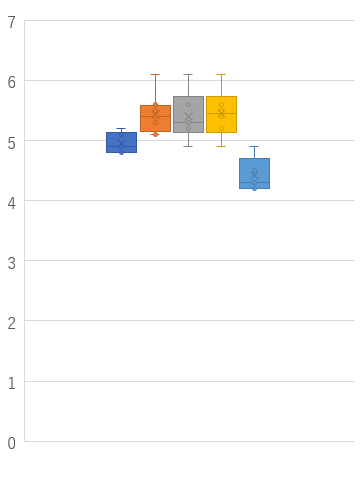
曜日別に検査の管理用資料を測定した。それぞれ総当たりで二標本t検定を行った。有意確率をBonferroni補正法を用いて有意水準５％で判定し有意な組み合わせをすべて記せ

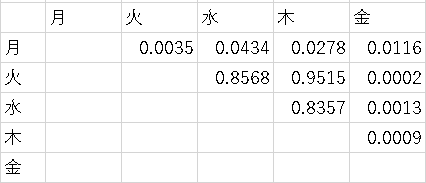
ここからは指標の話になっていきますが，検定ではなく９５％ＣＩ（信頼区間）で，その指標の意味合い（効果があると言えるのか）を確認する格好になります

研究法と相対リスク

観察研究(Observational study)

記述疫学
特段曝露について触れたものではない
ただし，人，場所，時間という曝露はあるが
記述統計と言われるものと同じ格好で，状況を可視化するもの
生態学的研究
集団レベルで曝露と疾病頻度の関係をみる．
仮説を形成するところまで
個人レベルで曝露と疾病頻度に関係が無くても集団レベルで行うと，関係が見えてくる場合がある　→　謎理論誕生
横断研究（Cross-sectional study）
曝露と疾患を同時に評価
時間軸がない場合が多く（例外は性別など）因果関係までは不明になってしまいやすい

コホート研究（Cohort study）
対象に曝露している人々と非曝露群を設定、追跡調査していくスタイル
通常前向きだが、後ろ向きにみる回顧的コホート研究というのもある。（後々でも曝露群に関する情報がある場合）

症例対照研究（Case-control study）
ある状態（例えば病気に罹患している）群と、罹患していない群を設定、時間を遡って調査していくスタイル
後ろ向きにしか行えない（前向きだと曝露→疾患の順がおかしくなる）

実験的研究（介入研究）（intervention study）

コホート研究の場合、曝露群（介入群）を研究者が割り付ける　→　被験者に対する倫理的配慮が肝要
無作為に割り付けることが出来る場合は交絡因子を制御できる（ことが期待される）
倫理的に考えると非介入群の方が不利益になってしまう可能性が高いので、配慮した研究デザインが求められる

説明用データ

	疾病発症	疾病無	計
曝露有	A	B	A+B
曝露無	C	D	C+D
計	A+C	B+D

リスク比

Risk Ratio(RR)
曝露（介入）の有る時と無の時の危険を示す指標の比
危険を示す指標には罹患率やら有病率やら死亡率やら

A～D:疾病発生頻度（頻度以外に罹患率やら有病率・・・）

曝露有群の発症リスク＝A/(A+B)
曝露無群の発症リスク＝C/(C+D)
リスク比＝A/(A+B)／C/(C+D)
もし、発生頻度が低ければA+B≒B　C+D≒D
　リスク比≒A/B／C/D＝AD/BC

オッズ比

Odds Ratio(OR)
危険な事象が起きた場合と起きなかった場合の指標の比（＝オッズ）について曝露（介入）の有無毎に求め比をとったもの

発症有群の曝露オッズ＝A/C
発症無群の曝露オッズ＝B/D
オッズ比＝A/C／B/D
　　　　＝AD/BC
上記のように発症頻度が低ければオッズ比とリスク比の近似値となる

問１１－２

適切な相対リスクの指標を算出せよ
以下はコホート研究のデータである

	不整脈あり	不整脈なし	計
曝露群	100	1900	2000
非曝露群	50	1950	2000
計	150	3850	4000

問１１－３

適切な相対リスクの指標を算出せよ
以下は症例対照研究のデータである

	不整脈あり	不整脈なし	計
曝露歴あり	100	65	165
曝露歴なし	100	135	235
計	200	200	400

問１１－４　なぜリスク比とオッズ比が乖離する場合があるのか簡潔に説明せよ

提出課題

本日の授業を受講したうえで，以下の2つの質問
１．理解できた内容，理解できなかった内容について
２．本日の授業の内容に関する質問（内容が概ね理解できているのであれば空欄でも可です）
を締切までに提出の事
締切は授業日翌日朝10時までとする

課題について

あれ？

オッズのほうが汎用性はあるかもしれないが、私たちが使うのはリスク比のほうが多いということが納得いかない

納得いかなくてよかったです．そんなことは申してなく，オッズの方をよく見かけるだろうという話．リスク比の方がそれぞれの群のリスクの比をとっているから説明しやすいという話

ネットで調べてもこの二つの比の使い分けは、前向き化後ろ向きの研究かどうかで変わるということがしっくりこない

前向きと後ろ向きで得られる集団の構成が異なるからと言ったらよいのかな？
以下のような書き込みが参考になるかと

症例対照研究でリスクが計算できないというのは、暴露歴があるかどうかで人を選んでいるのではなく、症状があるかどうかで人を選んでいるから

リスク比は基本正しいが、症例対照研究では、データの集め方がそもそも違うのでオッズ比を採用

このような理解で良いかと

リスク比は場合によって変わるが、オッズ比はほとんど変化がないことの理由

リスク比はそれぞれのリスクを求めないと計算できないが，症例対照研究のデータからそれぞれのリスクを求めることはできないですよね

えー！

やってないけど趣味で競馬を見ることが多いので（他にもゲームとかでよく見るので）、オッズの意味、計算方法が分かってすっきり

↓

競馬のオッズ計算はどうなっているの？初心者にも分かりやすく解説！（SIVA PRESS）
https://press.siva-ai.com/2018/11/30/1560/

オッズ比とリスク比がそもそもわからない

授業中に質問していただけますか

リスク比、オッズ比の求め方はわかったが、それらが意味することは分からない

意味が解らないと意味が無い

先週死ぬ気で勉強したのに既に忘れててやばい

死ぬ気で勉強すると知識にならないのでしょうね
未来がある若者ですから生き抜いていく気持ちで勉強してください

質問

オッズ比やリスク比で分母が0になった場合はどうなるの

比で出すのは困難ですね．差は出せますが

第12回　ROC解析

(教科書6章1,2,3)
教科書P115-
検査法の診断的有用性を評価する話

	疾患あり	疾患なし	指標
検査陽性	真陽性 a	偽陽性 b	陽性的中率 a/(a+b)
検査陰性	偽陰性 c	真陰性 d	陰性的中率 d/(c+d)
指標	感度 a/(a+c)	特異度 d/(b+d)	有病率 (a+c)/(a+b+c+d)

予測値

有病率の影響を受ける
陽性的中率＝P(Ｄ|陽性)
陰性的中率＝P(Ｄc|陰性)

感度と特異度

感度＝P(陽性|Ｄ) 　疾患群における真陽性の割合
偽陽性率＝P(陽性|Ｄc) 非疾患群における偽陽性の割合
特異度＝１－偽陽性率 非疾患群における真陰性の割合

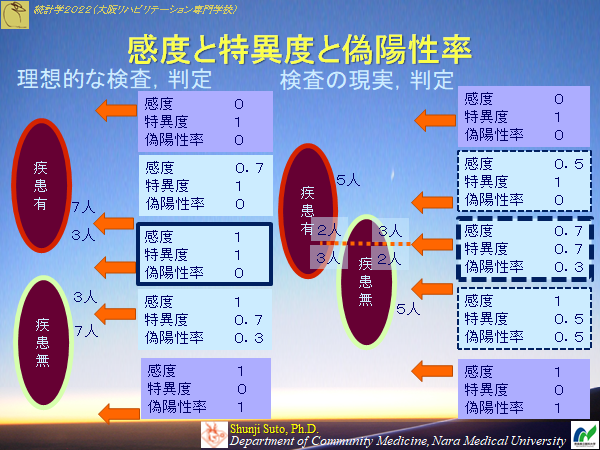
検査法の評価指標

AUC＝ROC曲線を描いて算出　検査の分別能

ROC曲線

教科書（P119）
判別度の分析
感度と偽陽性率（１－特異度）を用いて曲線を描く

カーブが左上に行くほど検査特性が優れている．（＝AUCが大きくなる）
判断基準は諸々の要素が入るが1,0と0,1の対角線と曲線の交わる部分が目安．あとは検査の目的などによって変わってくる

尤度比

教科書で尤度比としているのは陽性尤度比＝感度/偽陽性率

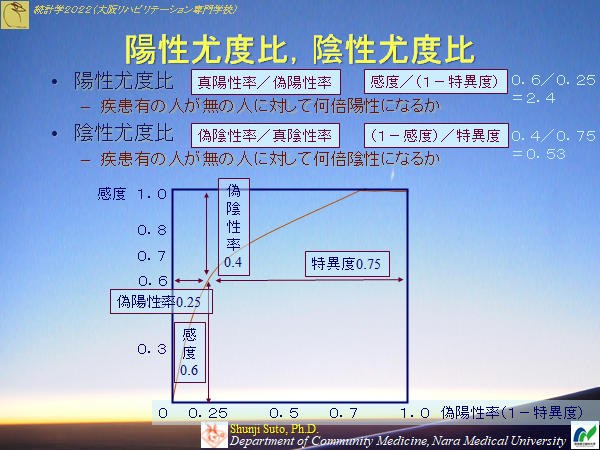
オッズ比

オッズ・・・値が高いほど感度が高い
オッズ比は疾患無しのオッズに比べ疾患有のオッズがどの程度高くなるのかの比

問１２－０１

2種類の検査法A,Bを施行したところ以下の結果を得た．
AUCを求めどちらの検査が優れているか評価せよ
また，作成の際には検査値を12.0~15.5まで0.5刻みで設定し評価のこと
A法

疾患群	14.3	15.2	13.8	14.1	13.9	12.6	14.2	14.6	13.1	13.7
非疾患群	13.2	14.1	13.8	13.6	12.9	12.4	12.1	12.3	12.3	12.8

B法

疾患群	14.3	15.2	13.8	14.1	13.9	12.6	14.2	14.6	13.1	13.7
非疾患群	13.2	14.3	13.8	12.9	14.4	14.4	12.1	15.3	12.3	12.8

解答例

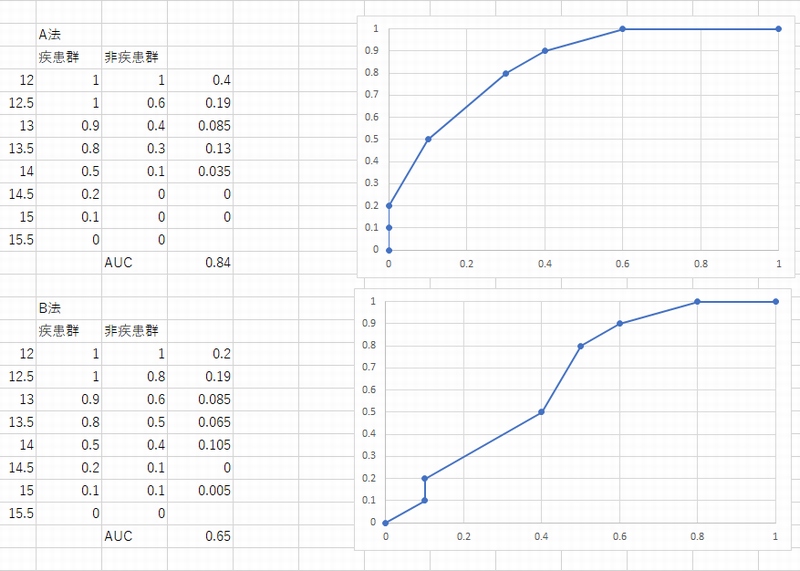
講義中にもう少し基準を細かく設定したら？という話が出たのですが，それぞれ出現した値以上で逐一求めたものは以下になります
より実態を示した結果になります

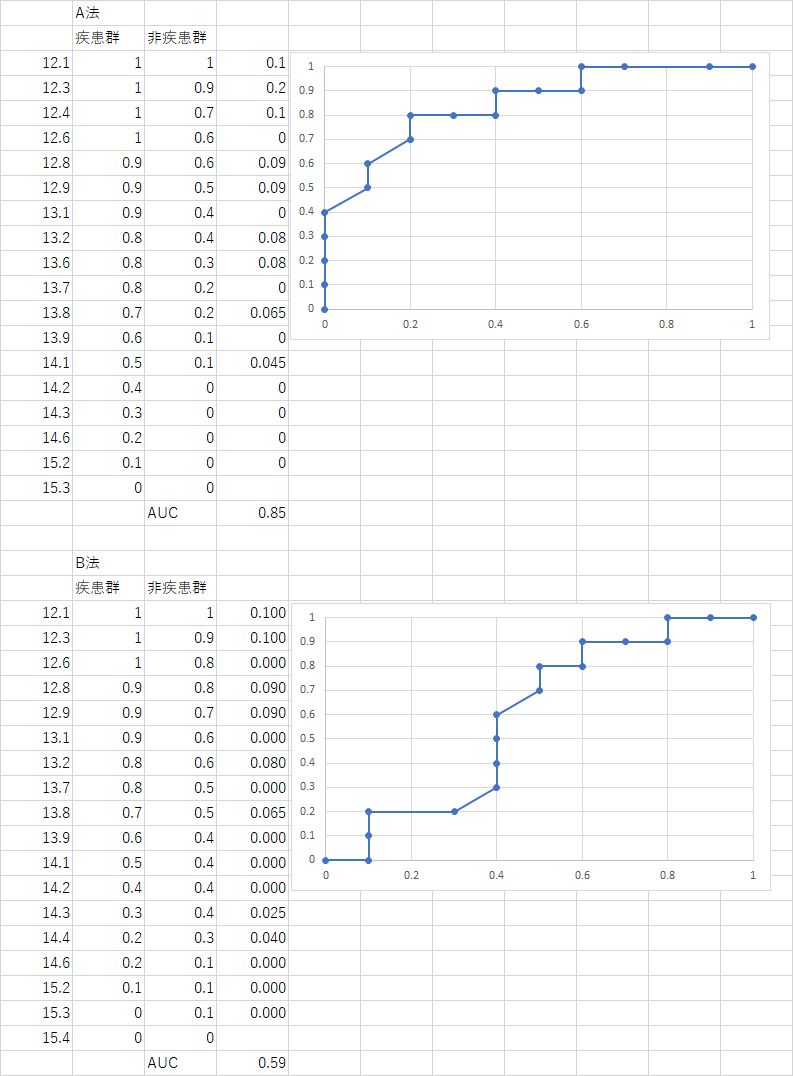
提出課題

本日の授業を受講したうえで，以下の2つの質問
１．理解できた内容，理解できなかった内容について
２．本日の授業の内容に関する質問（内容が概ね理解できているのであれば空欄でも可です）
を締切までに提出の事
締切は授業日翌日朝10時までとする

課題について

概ね大丈夫な話だったと思いますが

先週休んだら全然ついていけなかった

内容的には独立しているので先週休んだ話は関係ないように思うけど

AUCが大きいほど検査の性能が高い理由

曲線が左上に行くほどAUCは大きくなるから

ROC曲線という名前だが折れ線

生存曲線も仲間

いったいAUCの計算はどう行われているのか．どこにも記載がない．台形の面積を足すとよいらしいと分かったがもののかなり複雑

例年どおりでして，授業中に複数の台形に分解して計算する旨はお話ししておりましす
皆さんは様々な考え方で図形に分解しておりましたし，私はチャート紙の重さから求める方法なども話をしたと思います（無論授業では現実的ではりませんが）
教科書に掲載されて無いとのことで苦慮されたようですが，そこまでの説明は不要と筆者が判断していたからと思います
なお最終的に，ご自分で解決されたようですので，まさに復習を積極的に取り組み非常に良かったと思います（授業中に理解できなかった部分に取り組む）
なお授業中の状況などを鑑みて，以下のように説明を加えたケースもあります．台形の面積を足すのがややこしくないということをご理解いただけるかと思います（どのように切り分けると簡単に計算できるのか）
自分で考え手法や法則を見出すのが大学で求められる教育（学修）と捉えておりますが，それは皆さんが将来新たな知見に辿り着くための重要な部分になるもので，そのキッカケを奪ってはならないと考えているからです

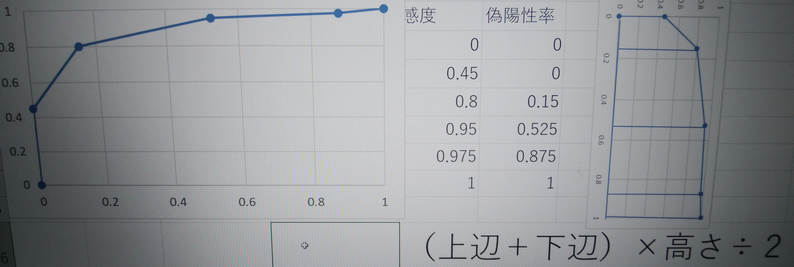
第3回　感度，特異度，ROC曲線（大阪リハビリテーション専門学校作業療法学科　統計学２０２２）　より

第13回　相関係数，回帰分析

【SO-02-03-04】相関分析、平均値と割合の検定等を実施できる。
【SO-02-03-05】多変量解析の意義を理解している。
(教科書9章1,2,3)

相関

correlative
相関関係がある・・・関連がある
相関関係が無い・・・関連がない
他方の影響を受けるか受けないか

因果

cause and effect
原因と結果
因果関係がある・・・影響がある
因果関係が無い・・・影響がない

普通は関連がある（相関がある）＝影響を及ぼす関係（因果関係がある）と考える（考えたくなる）
例
たばこを吸う－肺がん・・・・相関関係○

コーヒーを飲む－肺がん・・・相関関係○

コーヒーと肺がんの相関関係に割り込んでいる（どちらとも相関関係がある）状態＝交絡
割り込んでいるそれ＝交絡因子・・・たばこ
コーヒーと肺がんに因果関係が無いとしたならその関係は疑似相関

交絡因子について

教科書P220－

散布図

X軸とY軸に一つの対象に与えられるそれぞれの値をプロット（例：身長と体重）
とりあえず図にすると関係が直感的にわかる（場合がある）

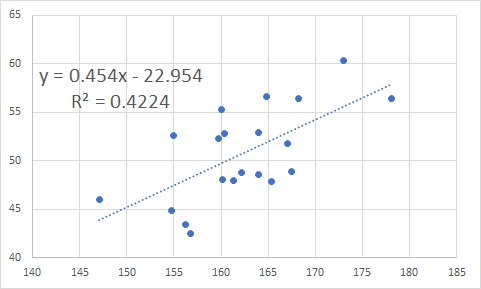
相関係数

-1から1までの値をとる
Xが増加すればYも増加する・・・1
Xが増加すればYは減少する・・・-1
Xが増加しようが減少しようがYは関係ない・・・0

X軸で見たときのバラツキ具合とY軸で見たときのバラツキ具合を元に計算してる
バラツキ＝散布度・・・分散・・・偏差の二乗の平均
共分散＝ある対象のX軸の偏差とY軸の偏差を乗じたものがベース
　　

Xの偏差	Yの偏差	乗じた結果
＋	＋	＋
＋	－	－
－	＋	－
－	－	＋

乗じた結果の平均が共分散
共分散はX軸Y軸のバラツキ具合が混ざっているのでそのままの数字だと解釈しにくい→XとYの標準偏差で除する（正規化）→相関係数

単相関係数の検定

P180-

問１３－１　例題７－４のデータより介入前と介入後の相関係数を求めよ（検定も行うこと）

回帰直線

X軸の値とY軸の値を数式（y=ax+b）で示す
直線を引いたときにそれぞれの点からの差（残差）の2乗して足したもの（平方和）が最も小さい時の数式が回帰直線

単回帰分析

教科書P195
回帰係数・・・Y=a+bXのb
決定係数・・・１に近いほど良好なモデル

決定係数

相関係数を二乗したもの
数式によって説明できる割合を示す。（寄与率とも）
高ければ高いほど数式で説明出来る

傾きの推定

傾きの推定値が0を含まないと，その項の変数（独立変数）はｙ（従属変数）にどのような影響を与えているのか説明できる

推定は計算機に

単回帰分析（t検定と信頼区間）作者: tonagai さん（ke!san）
https://keisan.casio.jp/exec/user/1491997364

重回帰分析

教科書P223
（回帰直線の話を思い出す→単回帰分析）
回帰・・・元に戻る・・・何らか（定理や関係）に基づき戻っていく
変数ごとに有意差検定を行っても他の変数の影響が含まれてしまう
予測モデル式としての話とどのような変数が影響を与えているのか

重回帰分析

Y=a+b1X1+b2x2+・・・ 目的変数・・・Y
説明変数・・・Xi
偏回帰係数・・・bi
標準偏回帰係数　β^*　目的変数と説明変数の関係を標準化したときの偏回帰係数・・・
目的変数は量的
説明変数は量的でも質的（0,1）でも
単回帰と同じく最小二乗法で求める
決定係数・・・説明変数を増やすと値は上昇 自由度調整済み決定係数・・・1-(1-R²)(n-1）/（n-k-1） n=標本数　k=独立変数

VIF　分散拡大要因

多重共線性を見つける指標
多重共線性・・・独立変数が他の独立変数と相関がある・・・偏回帰係数の標準誤差増大
VIF=(1-Ri²)^-1
Ri²：他の独立変数で重回帰させたときの決定係数
許容度：1-Ri² 目安としてVIFは10以下であること＝許容度が0.10を超えていること

分散分析

回帰式による変動と残差（回帰式と実測の差）の変動が異なるのか示している
異なると言えなければその回帰式は統計的に・・・

ロジスティック回帰モデル

目的変数を質的変量で重回帰分析できないのかな？という話
（あり・なし）の結果を確率で

ロジット変換

事象の起こる確率をpとしたときその取るべき値は0～1のいずれか．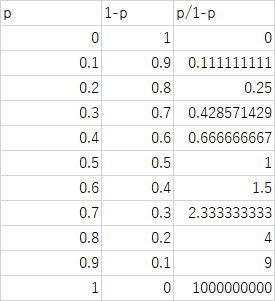


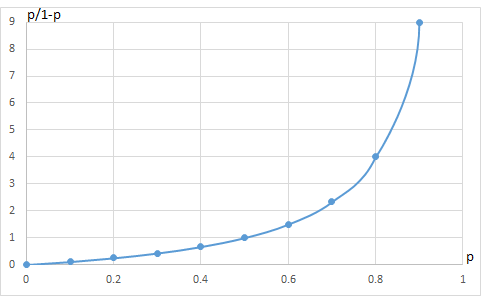
ロジット関数は，その確率の範囲を-∞～∞に拡張するもので logit(p)=ln(p)-ln(1-p)=ln(p/(1-p))で示される．


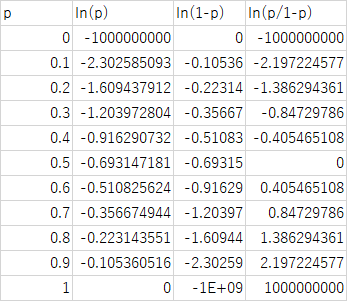
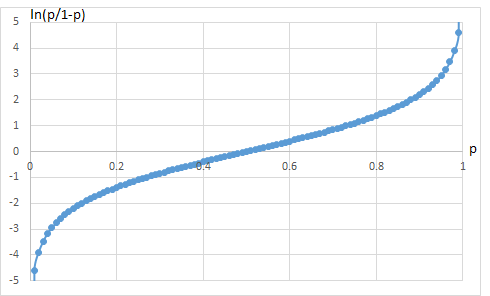
オッズを確率pで示すと
A/C=A/（A+C)／C/（A+C)=p/(1-p)
p=A/（A+C)であるが，その取りうる値は0～1．

pをロジット変換するとln(p)-ln(1-p)=ln(p/(1-p))

ln(p/(1-p))=a+b1X1+b2x2+・・・

exp(b)がオッズ比になる件

ln(p/(1-p))=a+b1x1+b2x2
とした場合
上記は
(p/(1-p))=exp(a+b1x1+b2x2+・・・)
=exp(a)*exp(b1x1)*exp(b2x2)*・・・

exp(b2)が1よりも大きい場合オッズは上昇し，1未満であれば低下する
式を整理すると
exp(b2x2)=(p/(1-p))/exp(a+b1x1+・・・)
となりexp(b2)はオッズ比を示す

問１３－２　以下の分析結果よりどのような因子が影響を受けているのか示せ

重回帰分析

パネル調査（ダミー）のデータより，自身の年収（ZQ47Aの回答を年収に変換）がどのような因子（普段の生活）によって影響を受けるのか分析した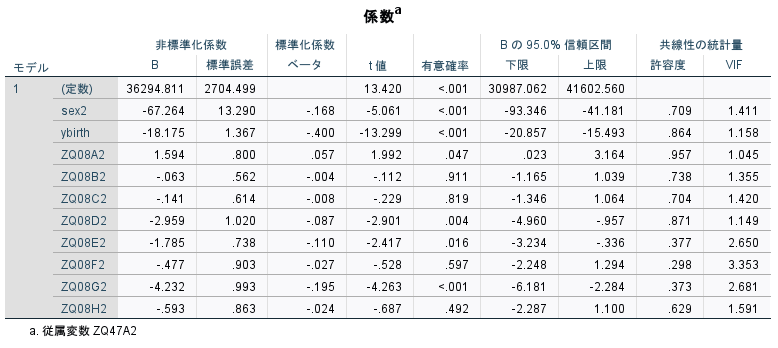

ロジスティック回帰分析

パネル調査（ダミー）のデータより，自身の健康状態（ZQ25が1と２を良好と定義）がどのような因子（普段の生活）によって影響を受けるのか分析した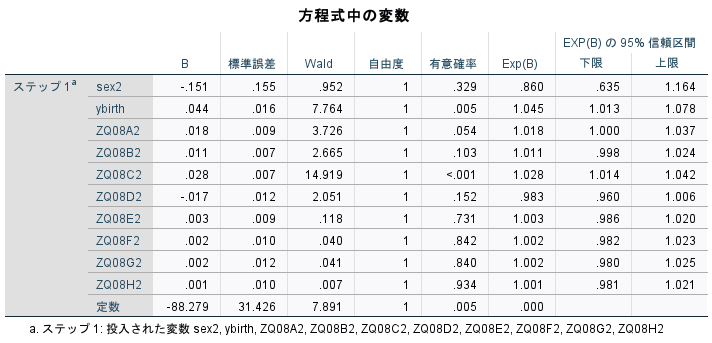

分析例で用いたデータ

非制限公開擬似データの提供（東京大学社会科学研究所附属社会調査・データアーカイブ研究センター）
https://csrda.iss.u-tokyo.ac.jp/infrastructure/urd/

提出課題

本日の授業を受講したうえで，以下の2つの質問
１．理解できた内容，理解できなかった内容について
２．本日の授業の内容に関する質問（内容が概ね理解できているのであれば空欄でも可です）
を締切までに提出の事
締切は授業日翌日朝10時までとする

課題について

簡単系

コンピュータで計算すればあとは表から読み取るだけなので簡単

重回帰分析などは実際自身で計算することは無いでしょう

悔しい系

相関係数は共通テストで何回も求めてきたのに、忘れかけていて悔しい

納得系

お金持ちで部屋が汚い人はあまり見たことがないので、家を掃除すると収入が減るということには驚くものの，見方によっては家事を手伝う手伝わないに関わるので納得

見方によってデータの見方が変わることが分かった

どのように解釈するかですよね．そのためには変数間の関係性を把握していないと適切な解釈に辿り着かない

複雑系

医学っぽくなった。難しいけど頑張る

例題7-4でt検定だと帰無仮説は棄却されるが、相関係数を使うと判定保留となるのは疑問に思ったというか意味を理解していないのかも知れない

例題７－４で明らかにしたいことに対してどのような分析が適当なのかという話になりますよね

物事の因果関係というのはあくまで一意に決めることのできないものではある。しかし今現在人々は表面的な答えを追い求めたがる。この世はそんなに単純ではない。

ありがとうございます

第14回　生存時間分析

【SO-02-02-02】割合・比・率の違い及び代表的な疫学指標（有病割合、リスク比、罹患率等）を理解している。
生存時間分析は治療法等の評価に時間軸を含めたもの
イベント発生までの時間による分析

比と率と割合（比率）

割合（比率）

proportion
全体に対してその一部がどの程度占めるか割ったもの・・・単位は無次元になる
０～１の間の値をとるpercentで表示したりする。100%を超えるのは本来おかしい
例）日本人の血液型の割合
A型　約40%
B型　約20%
O型　約30%
AB型　約10%

比

ratio
異なるもので割ったもの・・・単位は無次元の場合もある
例）BMI(Body Mass Index)
身長の二乗（m^2）に対する体重(kg)の比
身長170cmで体重70kgの人のBMI・・・７０／（１．７＾２）≒２４．２
検査表の見方（日本人間ドック学会）
http://www.ningen-dock.jp/public/method

率

rate
時間に対する何かの量の比・・・単位は無次元の場合もある
変化を表す指標
例）時速
マラソン（42.195km）を2時間6分で走った場合の時速・・・４２．１９５／２．１≒２０．１km/h
100m走を10秒で走った場合の時速・・・０．１／（１０／３６００）＝３６km/h

無次元の例としては稼働率
稼働率（JIT基本用語集）
http://www.lean-manufacturing-japan.jp/jit/cat241/post-74.html
時間を時間で割るので無次元

人年の計算法

死亡率を例として
一人の人を一年観察したとき１人年
人年に対する何かの量の比・・・率になる
例）5人の患者を1年間観察していた時に二人死亡
Aさん　1年後生存
Bさん　3ヶ月後に死亡
Cさん　9ヶ月後に死亡
Dさん　1年後生存
Eさん　1年後生存
＜本来の死亡率算出＞
観察人年＝1+0.25+0.75+1+1=4人年
その間の死亡数が２なので
2/4=0.5/年「1人年対0.5の死亡率」
＜年央人口を用いる方法だと＞
6ヶ月経過の時点での生存者4人
1年経過後の集団の死亡数が２なので
2/4=0.5/年「1人年対0.5の死亡率」

疾病頻度測定の指標

罹患率・・・率
累積罹患率・・・割合
有病率（時点有病率）・・・割合
期間有病率・・・割合
死亡率・・・率
致命率・・・比もしくは割合

＜参考＞
厚生労働統計に用いる主な比率及び用語の解説（厚生労働省）
http://www.mhlw.go.jp/toukei/kaisetu/index-hw.html
人年法の計算と利用方法,青木伸雄,日本循環器管理研究協議会雑誌 26(1),64-66,1991
https://www.jstage.jst.go.jp/article/jjcdp1974/26/1/26_1_64/_article/-char/ja/

生存率

生存率には計算方式が複数
電算機の普及によりKaplan-Meier法でも容易に計算出来る時代
そもそも率は比の特殊な形態で単位時間あたりのイベント数を表わす
Kaplan-Meierで求める非イベント発生（生存）率＝1-イベント発生（死亡）率そのものは、率では無く時点のイベント発生（死亡）割合なので注意

生存率の定義

実測生存率

イベント＝死亡として算出

補正生存率

イベント＝対象とする疾患での死亡として算出
対象としない疾患等での死亡は打切り扱い

相対生存率

実測生存率と期待生存率の比とも言えるが，割合（％表記）で用いられる
＜参考＞国がん　がん５年相対生存率は68.6％　乳がんなど3部位で9割超え（ミクスOnline）
https://www.mixonline.jp/tabid55.html?artid=70189

生存率の計算方法

直接法

観察期間終了時点（例　5年）での生存患者の割合を求める．
終了時点での追跡できた生存患者が全て？（中途打切り＝生存？死亡？）

生命保険数理法

年などで区切り区間ごとの死亡率を求め累積生存率を求める
イベントが発生した場合の生存期間（観察期間）は期間の半分まで（期待値）
＜参考＞
打ち切りの反映－計算方法は、技術の進化に応じて見直すべきか?（ニッセイ基礎研究所）
https://www.nli-research.co.jp/report/detail/id=57317?site=nli

Kaplan-Meier法

生命保険数理法が観察期間を区切っていたことに対して，実際にはイベント発生毎に算出
計算の回数が多くなるので大変・・・コンピュータの活用で解決
とはいっても，分単位での記録は難しいものが多いのではいか？
＜参考＞
生存時間データの解析（赤澤宏平　医療情報学/20 巻 (2000) 6 号）
https://www.jstage.jst.go.jp/article/jami/20/6/20_451/_article/-char/ja/
患者の生存率（地域がん登録全国協議会）
http://www.jacr.info/about/survival.html

Kaplan-Meier法による生存曲線の作成

個票データ
ここでは月単位のデータでしか取れなかったという恰好で

患者ID	診断名	観察終了時期	患者ID	診断名	観察終了時期	患者ID	診断名	観察終了時期	患者ID	診断名	観察終了時期	患者ID	診断名	観察終了時期
1	b	3	11	a	8	21	b	9	31	b	24+	41	a	3+
2	b	5	12	b	14	22	b	18	32	a	12	42	b	8
3	b	6	13	b	9	23	a	12+	33	a	3+	43	b	24+
4	b	14	14	a	1	24	a	3	34	b	13	44	a	5+
5	a	7+	15	a	2	25	b	17+	35	b	17	45	b	14
6	a	14	16	a	3	26	a	7	36	a	3
7	a	17	17	a	13	27	a	8	37	b	15
8	b	21	18	b	21	28	a	12	38	b	13
9	b	21	19	b	16	29	b	12+	39	a	21
10	b	16	20	b	24+	30	a	1	40	b	18

+は打ち切り

生存率の計算

疾患a

診断からの月数	月開始時の生存数	死亡数	中途打ち切り数	死亡割合	生存割合	累積生存率
1	20	2	0	0.100	0.900	0.900
2	18	1	0	0.056	0.944	0.850
3	17	3	2	0.176	0.824	0.700
5	12	0	1			0.700
7	11	1	1	0.091	0.909	0.636
8	9	2	0	0.222	0.778	0.495
12	7	2	1	0.286	0.714	0.354
13	4	1	0	0.250	0.750	0.265
14	3	1	0	0.333	0.667	0.177
17	2	1	0	0.500	0.500	0.088
21	1	1	0	1.000	0.000	0.000

疾患b

診断からの月数	月開始時の生存数	死亡数	中途打ち切り数	死亡割合	生存割合	累積生存率
3	25	1	0	0.040	0.960	0.960
5	24	1	0	0.042	0.958	0.920
6	23	1	0	0.043	0.957	0.880
8	22	1	0	0.045	0.955	0.840
9	21	2	0	0.095	0.905	0.760
12	19	0	1			0.760
13	18	2	0	0.111	0.889	0.676
14	16	3	0	0.188	0.813	0.549
15	13	1	0	0.077	0.923	0.507
16	12	2	0	0.167	0.833	0.422
17	10	1	1	0.100	0.900	0.380
18	8	2	0	0.250	0.750	0.285
21	6	3	0	0.500	0.500	0.143
24	3	0	3			0.143

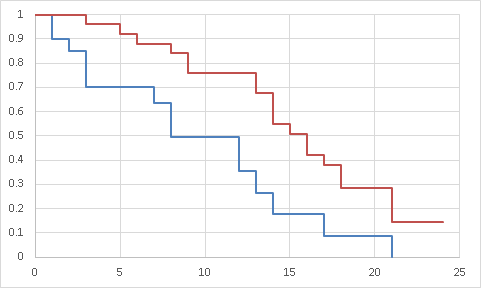
疾患a：青線
疾患b：赤線

ログランク検定

カイ二乗分布による検定を行う
（期待度数と比較してバラツキがあるか否か）

イベント発生毎のクロス表（カッコ内は期待度数）

１ヶ月

	死亡数	生存数	合計
症例a	2(0.889)	18(19.111)	20
症例b	0(1.111)	25(24.889)	25
合計	2	43	45

２ヶ月

	死亡数	生存数	合計
症例a	1(0.419)	17(17.581)	18
症例b	0(0.581)	25(24.419)	25
合計	1	42	43

以下同様な格好で観測度数と期待度数（例：期待死亡数）を求めていく

観察度数及び期待度数

診断からの月数	a観察度数	a打ち切り数	a総人数	a期待度数	b観察度数	b打ち切り数	b総人数	b期待度数
1	2	0	20	0.889	0	0	25	1.111
2	1	0	18	0.419	0	0	25	0.581
3	3	2	17	1.619	1	0	25	2.381
5	0	1	12	0.333	1	0	24	0.667
6	0	0	11	0.324	1	0	23	0.676
7	1	1	11	0.333	0	0	22	0.667
8	2	0	9	0.871	1	0	22	2.129
9	0	0	7	0.500	2	0	21	1.500
12	2	1	7	0.538	0	1	19	1.462
13	1	0	4	0.545	2	0	18	2.455
14	1	0	3	0.632	3	0	16	3.368
15	0	0	2	0.133	1	0	13	0.867
16	0	0	2	0.286	2	0	12	1.714
17	1	0	2	0.333	1	1	10	1.667
18	0	0	1	0.222	2	0	8	1.778
21	1	0	1	0.571	3	0	6	3.429

検定統計量χ^2＝Σ（ＯiーＥi）^2／Ｅi

今回は二つの群の比較・・・自由度k＝n-1=1
Ｏ1＝a観察度数の総和=15
Ｅ1＝a期待度数の総和=8.549
Ｏ2＝b観察度数の総和=20
Ｅ2＝b期待度数の総和=26.451
検定統計量χ^2＝6.441
χ^2（1,0.95）=3.8415
故に帰無仮説を棄却し対立仮説を採択する（a,bの再発率に差がある）

問１４－１

次のデータからカプランマイヤー法により生存確率を推定し生存曲線を描き，疾患ABによる違いがあるか検定せよ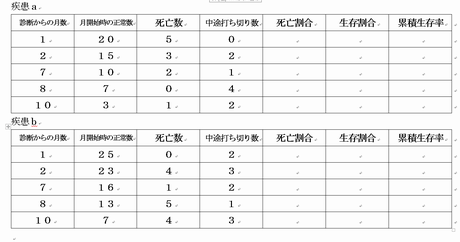

提出課題

本日の授業を受講したうえで，以下の2つの質問
１．理解できた内容，理解できなかった内容について
２．本日の授業の内容に関する質問（内容が概ね理解できているのであれば空欄でも可です）
を締切までに提出の事
締切は授業日翌日朝10時までとする