撧椙導棫堛壢戝妛丂惗暔摑寁妛俀侽侾俇
乮堛妛晹堛妛壢乯
杮庼嬈偺埵抲晅偗
堛妛嫵堢儌僨儖丒僐傾丒僇儕僉儏儔儉乛弨旛嫵堢儌僨儖丒僐傾丒僇儕僉儏儔儉乮暯惉22擭搙夵掶斉乯傪儀乕僗偵峔惉http://www.mext.go.jp/b_menu/shingi/chousa/koutou/033-1/toushin/1304433.htm
杮島媊偑弨旛嫵堢儌僨儖丒僐傾丒僇儕僉儏儔儉偵偍偄偰扴偆晹暘
俁忣曬偺壢妛
丂乮俀乯摑寁偺婎慴
丂丂妋棪榑揑側傕偺偺尒曽傪棟夝偟丄妋棪曄悢偲偦偺暘晍丄悇應揑悇寁偺尨棟偲曽朄傪棟夝偡傞丅
丂乮俁乯摑寁庤朄偺揔梡
丂丂堛妛惗暔妛偱傛偔憳嬾偡傞昗杮偵丄摑寁庤朄傪揔梡偡傞偲偒偵惗偠傞栤戣揰傗摑寁僷僢働乕僕偺棙梡傪娷傔偨嬶懱揑側埖偄曽傪廗摼偡傞
埲壓丄杮島媊偱堛妛嫵堢儌僨儖丒僐傾丒僇儕僉儏儔儉偺拞偱娭楢偡傞崁栚
乽A婎杮帠崁乿
俀堛椕偵偍偗傞埨慡惈妋曐
丂乮侾乯埨慡惈偺妋曐
丂丂係乯堛椕偺埨慡惈偵娭偡傞忣曬傪嫟桳偟丄帠屻偵栶棫偰傞偨傔偺暘愅偺廳梫惈傪愢柧偱偒傞
係壽戣扵媶丒夝寛擻椡
丂乮俁乯堛妛尋媶傊偺巙岦偺熂梴
丂丂俁乯姵幰傗幘姵偺暘愅傪傕偲偵丄嫵壢彂丒榑暥摍偐傜嵟怴偺忣曬傪専嶕丒惍棟摑崌偟丄幘姵偺棟夝丒恌抐丒帯椕偺怺壔偵偮側偘傞偙偲偑偱偒傞丅
丂丂係乯専嶕丒専弌偟偨堛妛丒堛椕忣曬偐傜怴偨側壽戣丒壖愢傪愝掕偟丄夝寛偵岦偗偰壢妛揑尋媶乮椪彴尋媶丄塽妛尋媶丄惗柦壢妛尋媶摍乯偵嶲壛偡傞偙偲偑偱偒傞丅
丂乮俆乯堛椕偺昡壙丒専徹
丂丂侾乯壢妛揑崻嫆偵婎偯偄偨堛椕偺昡壙偲専徹偺昁梫惈傪愢柧偱偒傞丅
乽B堛妛丒堛椕偲幮夛乿
丂乮俀乯抧堟堛椕
丂丂侾乯抧堟幮夛偵偍偗傞堛椕偺忬嫷丄婡擻偍傛傃懱惂摍傪娷傔偨抧堟堛椕偵偮偄偰奣愢偱偒傞丅
丂丂俀乯堛巘偺曃嵼乮抧堟媦傃恌椕壢乯偺尰忬偵偮偄偰愢柧偱偒傞丅
丂乮俁乯塽妛偲梊杊堛妛
丂丂俁乯幘昦丒桳昦丒彎奞摑寁丄擭楊挷惍棪偲昗弨壔巰朣斾傪愢柧偱偒傞丅
丂乮俉乯椪彴尋媶偲堛椕
丂丂係乯尋媶僨僓僀儞傪奣愢偱偒傞
庼嬈儊僯儏乕
戞1夞丂僆儕僄儞僥乕僔儑儞
戞2夞丂広搙丒搙悢暘晍
戞3夞丂戙昞抣丒嶶晍搙
戞4夞丂暯嬒抣偺悇掕
戞5夞丂憡娭學悢丒夞婣捈慄
戞6夞丂姶搙丒摿堎搙丒ROC嬋慄
戞7夞丂憡懳婋尟搙
戞8夞丂専掕偺尨棟
戞9夞丂僷儔儊僩儕僢僋専掕
戞10夞丂僲儞僷儔儊僩儕僢僋専掕
戞11夞丂寁悢抣僨乕僞偺専掕
戞12夞丂撈棫懡孮娫偺斾妑
戞13夞丂懡曄検夝愅
戞14夞丂惗懚帪娫暘愅
戞15夞丂傑偲傔
戞1夞丂僆儕僄儞僥乕僔儑儞
摓払栚昗侾亅侾庼嬈偺奣梫傪愢柧偱偒傞
侾亅俀摑寁偺庬椶偵偮偄偰愢柧偱偒傞
侾亅俁僨乕僞偺壜帇壔偺昁梫惈偵偮偄偰愢柧偱偒傞
杮庼嬈偺栚揑
丂惗暔摑寁妛偼丄摑寁揑庤朄傪梡偄偰曐寬堛椕暘栰偵偍偗傞壽戣偺夝寛偵帒偡傞妛栤椞堟偱偁傞丅偦偺偨傔摑寁妛偺婎慴偩偗偱偼側偔丄偙傟傑偱杮暘栰偵偍偄偰偳偺傛偆側摑寁揑庤朄偑梡偄傜傟偰偒偨偺偐棟夝偟丄僨乕僞偺廂廤丒夝愅丒夝庍傪幚巤偡傞嵺偵嵟揔側庤朄傪慖戰偡傞偨傔偺抦幆偲丄偦傟傪妶梡偡傞擻椡偺妉摼傪栚揑偲偡傞丅
杮庼嬈偺摓払栚昗
侾乯僨乕僞偺惈幙偵娭偟偰愢柧偱偒傞俀乯揔愗側摑寁庤朄傪慖戰偱偒傞
俁乯壖愢偺摑寁妛揑専掕朄傪愢柧偱偒傞
係乯尋媶僨僓僀儞枅偺摿挜偲僨乕僞傪庢傝埖偆忋偱偺拲堄揰傪愢柧偱偒傞
侽乯摑寁庤朄側偳昁梫偵墳偠偰乽曌嫮偡傟偽弌棃傞傛偆偵側傞擻椡乿傪妉摼偡傞
嫵壢彂
僇儔乕僀儊乕僕偱妛傇亙怴斉亜摑寁妛偺婎慴http://www.nikkyoken.com/pub/edu.html
嶲峫恾彂
僶僀僆僒僀僄儞僗偺摑寁妛亅惓偟偔妶梡偡傞偨傔偺幚慔棟榑http://www.nankodo.co.jp/g/g9784524220366/
嶲峫帒椏
昁梫偵墳偠偰揔媂攝晍偟傑偡庼嬈偺恑傔曽
揹戩巊偄傑偡偺偱傛傠偟偔偍婅偄偟傑偡乮庼嬈拞偼僗儅儂偱壜偱偡偑帋尡偺帪偼亊乯
statflex偼庼嬈拞巹偟偐巊偊側偄偺偱丄夋柺尒偰偔偩偝偄
婰弎摑寁偲悇應摑寁
摑寁偲偼俀偮埲忋偺梫慺偺廤傑傝偐傜側傞廤抍偺摿惈傪柧傜偐偵偡傞偙偲廤抍偺摿惈佮屄乆偺摿惈丂偲偄偆峫偊曽丅幚嵺偵偼丂廤抍偺摿惈亗屄乆偺摿惈丂偺働乕僗傕懡偄
婰弎摑寁妛
僨乕僞偺廤抍偑壗傪帵偡偺偐乮庢傝埖偆僨乕僞偑慡偰乯搙悢暘晍丒戙昞抣丒嶶晍搙
悇應摑寁妛
悇掕偲専掕偵暘偐傟傞偳偪傜傕庢傝埖偆僨乕僞偼柧傜偐偵偟偨偄慡懱偺堦晹暘偲側傞
悇掕
僨乕僞偑壗傪帵偡偺偐丂堦晹偺僨乕僞傪懳徾丂 仺丂慡懱傪悇應
専掕
僨乕僞偑偳偺傛偆側忬嫷偐丂梌偊傜傟偨僨乕僞傪懳徾丂仺丂専徹丒丒丒枹棃梊應
椉幰偼枾愙偵娭楢偟偰偄傞
摑寁僨乕僞偺棙妶梡
僗儅儂偺埵抲僨乕僞
yahoo傾僾儕偺棙梡忬嫷傪抧恾忋偵昞帵
搶擔杮戝恔嵭娭楢偺擔偺搶嫗嬤曈
岞奐偝傟偰偄傞帪宯楍僨乕僞
僌儔僼偱恾帵壔偡傞偲僩儗儞僪偑椙偔傢偐傞暯惉27擭斉丂忣曬捠怣敀彂乮憤柋徣乯
搶擔杮戝恔嵭慜屻偺抧恔僨乕僞偺壜帇壔丅僌儔僼偩偗偱側偔抧棟忣曬傪娷傔傞偲忬嫷偑椙偔傢偐傞
http://chihochu.jp/52515696/
搶擔杮戝恔嵭偺
朰傟側偄乣恔嵭媇惖幰偺峴摦婰榐
摓払搙妋擣
侾乯婰弎摑寁偲悇應摑寁偵偮偄偰傑偲傔傛庼嬈屻曗懌
|
徯夘偟偨儕儞僋愭偺儁乕僕偺抧恔偵娭偡傞摑寁僨乕僞偺壜帇壔偺晹暘偺傒尒偰捀偒傑偟偨丅 幚嵺偺塮憸偵娭偟偰偼峊偊傑偟偨丅偛帺恎偺敾抐偱偛棗偔偩偝偄丅 摑寁張棟偵傛傝岅傟傞偙偲丄尰応傪尒偰岅傟傞偙偲偺堘偄偵偮偄偰峫偊偰偍偄偰偔偩偝偄丅 壢妛揑崻嫆偼摑寁張棟偵傛傝偦傟偧傟偺屌桳偺愲偭偰偄傞晹暘偑柍偔側偭偰偟傑偆偺偱丄椪彴偱偼偦偺屌桳偺愲偭偰偄傞晹暘傪曗揢偟偰峫偊側偔偰偼偄偗側偄 慡悢挷嵏乮幓奆挷嵏乯偼楯椡偑偐偐偭偰戝曄乮崙惃挷嵏乯 |
戞2夞丂広搙丒搙悢暘晍
摓払栚昗俀亅侾僨乕僞偺広搙暘椶乮係偮偺広搙乯偵偮偄偰愢柧偱偒傞
俀亅俀搙悢暘晍昞偑嶌惉偱偒傞
俀亅俁昗杮偺拪弌偵傛偭偰寢壥偑曄傢傞偙偲傪愢柧偱偒傞
柤屆壆偐傜挿栰傑偱宷偑偭偰偄傞丅傑偝偵拞墰峔憿慄増偄丅嶐擔偺抧恔傛傝偼傞偐偵峀斖埻偱儅僌僯僠儏乕僪傕戝偒偄丅RT @dom_kyon: 斖埻峀偄 pic.twitter.com/3pKAYJD7qD
— 娾忋埨恎 (@iwakamiyasumi) 2016擭4寧15擔
亂巻柺亃恔尮堟 懷忬偵丅孎杮導丒戝暘導偺庡側旐奞偲抐憌懷丅傎偐 徻偟偔偼杮擔(4寧17擔晅)搶嫗怴暦挬姧偵偰丅 pic.twitter.com/hI9P8Vmd2b
— 搶嫗怴暦傎偭偲Web 僆僼傿僔儍儖 (@tokyohotweb) 2016擭4寧16擔
曣廤抍偲偼
懳徾偲偟偰偄傞廤抍偺慡懱傪巜偟帵偡偲偒偵乽曣乿傪嵟弶偵晅偗傞丅柍尷曣廤抍偲桳尷曣廤抍偐傜側傞丅
懳徾偑桳尷偐柍尷偵憹怋偡傞偐偺堘偄
昗杮偲偼
曣廤抍偺堦晹丅崺拵昗杮傪巚偄晜偐傋傞偲丄曃傝偵拲堄偡傞昁梫偑偁傞偙偲偼帺柧丅
嶲峫
昗杮挷嵏偼僒儞僾儖拪弌偑柦乮The Huffington Post Japan乯http://www.huffingtonpost.jp/nissei-kisokenkyujyo/sample-survey_b_5878832.html
椺乯暅尦拪弌偲旕暅尦拪弌
嬌抂側椺丒丒丒傾僞儕僇乕僪侾枃偲奜傟僇乕僪侾枃擖偭偨敔偐傜俀夞僇乕僪傪堷偔丒丒丒傾僞儖妋棪50%
暅尦拪弌丒丒丒傾僞儕偑弌傞妋棪75%乮僐僀儞僩僗偺傛偆側姶偠乯
旕暅尦拪弌丒丒傾僞儕偑弌傞妋棪100亾
侾侽枃偺偔偠乮偁偨傝2杮乯偐傜俆枃拪弌丅暅尦拪弌偟偨応崌偲旕暅尦拪弌傪偟偨応崌偺寢壥偺堘偄
梋択
妋棪偼帠慜忣曬偵傛偭偰曄壔偡傞仺儀僀僘棟榑儌儞僥傿儂乕儖栤戣
僱僐偱傕傢偐傞儌儞僥傿儂乕儖僕儗儞儅(DOFI-BLOG 偳傆偂傇傠偖)
偙偺応崌偼嵟弶偵慖傇僇乕僪偵娭偡傞忣曬偑梌偊傜傟偰偄側偄偙偲丅
俀夞栚偺慖戰偵偍偄偰忣曬偑梌偊傜傟偰偄傞偙偲丅
椪彴偵偍偄偰偼條乆側忣曬傪get偟側偑傜僇乕僪傪慖傫偱偄偔
曄検(僨乕僞)偺暘椶
曄検偼條乆側傕偺偑偁傞偑偦傟傜偺惈幙傪偲傝傑偲傔暘椶偡傞偙偲偑弌棃傞丅偦傟偧傟傪広搙偲屇傃丄4偮偵暘椶偡傞偺偑堦斒揑偱偁傞
侾暘椶広搙乮柤媊広搙乯
俀弴彉広搙
俁娫妘広搙
係斾広搙乮斾椺乯
侾丆俀傪幙揑曄検乮掕惈揑乯
俁丆係傪検揑曄検乮掕検揑乯
惈幙偲偟偰偼忋埵屳姺惈偑偁傝
係亜俁亜俀亜侾
嫵壢彂偼娫妘広搙媦傃斾広搙偵娭偟偰摑寁張棟忋嬫暿偡傞堄枴偼柍偄偲側偭偰偄傞偑丄拲堄偼昁梫
億僀儞僩偼悢妛揑偵偼惓偟偐偭偨偲偟偰傕堄枴揑偵惓偟偄偐偳偆偐
搙悢暘晍昞
偦傟偧傟偺僨乕僞乮曄検乯偺悢乮弌尰昿搙乯傪傑偲傔偨傕偺曄検偑柤媊広搙偺帪偼懡偄弴乮偍嶌朄偲偟偰丅扐偟偦偺懠傪弌偡側傜堦斣嵟屻乯
弴彉広搙埲崀偱偁傟偽弴乮柤媊広搙偱傕斾妑偺偨傔偵偍嶌朄傪攋傞偙偲偼偁傞乯
搙悢丂丂丒丒丒弌尰昿搙
椵愊搙悢丒丒丒忋埵偺曄検偺搙悢傕偁傢偣偨搙悢
憡懳搙悢丒丒丒憤弌尰昿搙傪1乮100%乯偲偟偨偲偒偵丄偦傟偧傟偺搙悢偑偟傔傞妱崌
椵愊憡懳搙悢丒丒丒椵愊搙悢偺憡懳斉
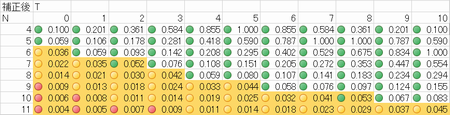
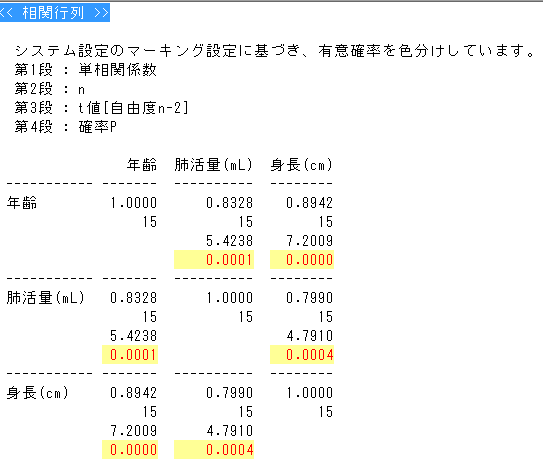
嫵壢彂P76偺A嵻偵傛傞擜検偺搙悢暘晍昞傪嶌惉偟偰偔偩偝偄
| 奒媺 | 奒媺抣 | 搙悢 | 憡懳搙悢 | 椵愊搙悢 | 椵愊憡懳搙悢 |
|---|---|---|---|---|---|
| 0.5乣1.0 | 0.75 | 5 | 0.167 | 5 | 0.167 |
| 1.0乣1.5 | 1.25 | 5 | 0.167 | 10 | 0.334 |
| 1.5乣2.0 | 1.75 | 12 | 0.4 | 22 | 0.734 |
| 2.0乣2.5 | 2.25 | 3 | 0.1 | 25 | 0.834 |
| 2.5乣3.0 | 2.75 | 3 | 0.1 | 28 | 0.934 |
| 3.0乣3.5 | 3.25 | 1 | 0.033 | 29 | 0.967 |
| 3.5乣4.0 | 3.75 | 1 | 0.033 | 30 | 1.00 |
| 寁 | ----- | 30 | 1.00 | ----- | ----- |
摓払搙妋擣
侾乯忋婰偺搙悢暘晍昞傪姰惉偝偣傛庼嬈屻曗懌
|
嫵壢彂奩摉儁乕僕 戞1復乮P10-P20乯 戞2復乮P22,P31乯 儌儞僥傿儂乕儖栤戣偺妛惗偺夞摎忬嫷 A慻丗 俀枃偵偟偨偲偒偵妋棪偑崅偔側傞傕偺偼丠 嵟弶偵慖傫偩曽丒丒丒俁柤 偳偪傜傕摨偠丒丒丒俀侽柤 慖傫偱側偄曽丒丒丒侾俀柤 俀枃偵側偭偨偲偒嵟弶偵慖傫偩傎偆偺妋棪偼丠 侾侽亾丒丒丒俀侽柤乮僇乕僪傪ABC俁枃偱偼側偔侾侽枃偱乯 俆侽亾丒丒丒侾侽柤 B慻丗 俀枃偵偟偨偲偒偵妋棪偑崅偔側傞傕偺偼丠 嵟弶偵慖傫偩曽丒丒丒俉柤 偳偪傜傕摨偠丒丒丒丒俉柤 慖傫偱側偄曽丒丒丒俀侾柤 乮俀侾柤偺撪偙偺榖傪抦偭偰偄偨妛惗侾係柤乯 宱堒傪攃埇偟偰偦偺忣曬傪妶偐偝側偄偲愜妏偺僠儍儞僗傪幐偆偲偄偆榖 偨偩偟丄偙傟偼妋棪偺榖偱偁偭偰丄 |
搙悢暘晍恾
搙悢暘晍昞傪僌儔僼壔偟偨傕偺廲朹僌儔僼偩偑検揑曄検偵尷偭偰偼乽僸僗僩僌儔儉乿偦偺朹偺晹暘偺柺愊偑搙悢傪帵偟偰偄傞
僗僞乕僕僃僗偺岞幃
検揑曄検偺搙悢暘晍昞丒恾嶌惉偺帪偵奒媺暆愝掕偺嶲峫偵側傞岞幃K乮奒媺悢乯亖1亄log2乮僒儞僾儖悢乯
僒儞僾儖悢偼14側偺偱
1+3.81=4.81
4乣5偖傜偄偑揔摉
忋婰傪嶲峫偵偟側偑傜奒媺暆傪寛傔傞偲傛偄乮偐傕掱搙偱乯
嶲峫丗僸僗僩僌儔儉偼晐偄亅僗僞乕僕僃僗偺岞幃乮崅峑悢妛偺栤戣傪嶌傞 亅岺晇丒僐僣偲僨乕僞亅乯
http://www10.plala.or.jp/mondai/columun/hist.pdf
乮宱尡懃偵婎偯偄偨傕偺偩偲偽偐傝巚偭偰偄偨偺偱價僢僋儕仺僂僃乕僶乕丒僼僃僸僫乕偺朄懃乯
恖娫偺屲姶偼懳悢偵曄姺偝傟偰偄傞乮偼傑偖傝偺悢妛乯
僑儖僑偺抧恔挻晐偄僐儔傪巚偄弌偡 pic.twitter.com/t44gJNqVA7
— 僫儖僷僕儞 (@narupajin) 2016擭4寧15擔
曗懌
|
嫵壢彂奩摉儁乕僕 戞1復乮P10-P20乯 戞2復乮P22,P31乯 |
戞3夞丂戙昞抣丒嶶晍搙
摓払栚昗俁亅侾戙昞抣偺嶼弌媦傃摿惈偵偮偄偰愢柧偱偒傞
俁亅俀嶶晍搙偺嶼弌媦傃摿惈偵偮偄偰愢柧偱偒傞
戙昞抣偲嶶晍搙偲戝偒偝n乮屄悢傗帠徾悢乯偑採帵偝傟傟偽丄偦偺廤抍偑偳傫側傕偺偐憐憸弌棃傞乮儅儔僜儞幚嫷乯
戙昞抣
average乮偦偺廤抍傪悢抣堦偮偱昞偡丅excel偼average娭悢偱嶼弍暯嬒傪弌偡偑丄傑偀戙昞抣偺戙昞偲偄偆偙偲偩偐傜偲夝庍偟偰偄傑偡乯嶼弍暯嬒
mean乮嶼弍暯嬒埲奜偵傕憡忔暯嬒乮愊偟偰椵忔崻傪偲傞乯側偳傕偁傝傑偡乯1/n丒儼xii
惓幮堳抝惈偺暯嬒媼梌乽527枩墌乿丂堷偒忋偘偰偄傞偺偼扤側偺偐丠乮BLOGOS-僉儍儕僐僱僯儏乕僗2014擭10寧04擔乯
http://blogos.com/article/95831/
僷儗乕僩偺朄懃乮80-20偺朄懃乯
戙昞抣側偺偵幚嵼偟側偄応崌偑偁傞丂仺丂廤抍偺巜昗偱偁偭偰丄戙昞偡傞帠徾傪帵偟偰偄傞偲偼尷傜側偄
搙悢暘晍昞傪婎偵偟偨暯嬒抣偺寁嶼朄偵偮偄偰
儼乮奒媺抣亊搙悢乯乛娤應悢
拞墰抣
median乮暿柤戞俀巐暘埵悢乯検揑曄検傪弴彉広搙偱張棟偟偨戙昞抣
弴斣偵暲傋偨偲偒恀傫拞偺弴埵偵偒偨屄懱偺抣
屄懱悢偑嬼悢偺帪偼恀傫拞2偮偺悢抣偺暯嬒抣
僗僉乕僕儍儞僾偺旘宆揰偼拞墰抣揑側僲儕偱嶼弍暯嬒偟偰偄傞
僗僉乕僕儍儞僾傪抦傠偆両両儖乕儖夝愢乮僕儍儞僾愥報儊僌儈儖僋乯
https://www.meg-snow.com/jump/rule/rule.html
嵟昿抣
mode乮棳峴丆偼傗傝乯堘偆堄枴偱悢偺棟榑乮懡悢寛乯偺悽奅
検揑曄検傪柤媊広搙偱張棟偟偨戙昞抣
柤媊広搙偱傢偐傞偙偲偼堦弿偐堘偆偐
奒媺枅偵搙悢傪僇僂儞僩
堦斣懡偄偲偙傠偺奒媺抣
堦埵偑摨揰偺帪偼暪婰乮暯嬒傪偲傞偲丂偊偭僆儗桪彑両丠忬懺偵側傞乯
嶶晍搙
dispersion嵟戝抣偲嵟彫抣傪巊偆
嵟戝抣偲嵟彫抣偑傢偐傟偽偦偺廤抍偺僶儔僣僉偑傢偐傞嵟戝抣maximum excel max娭悢
嵟彫抣minimum excel min娭悢
斖埻
RangeR=嵟戝抣亅嵟彫抣
摿挜
丂奜傟抣傕傂傜偆
丂嶼弌偑梡堄
巐暘埵悢傪巊偆
Quartile彫偝偄弴乮徃弴乯偵暲傋偰廤抍傪4暘妱
戞侾巐暘埵悢 First Quartile:Q1 =丂25th percentile 25%僞僀儖抣
戞俀巐暘埵悢 Second Quartile:Q2 = 50th percentile 50%僞僀儖抣丂亖丂Median丂拞墰抣
戞俁巐暘埵悢 Third Quartile:Q3 =丂75th percentile 75%僞僀儖抣
巐暘埵悢偺媮傔曽丒丒丒尩枾偵偼悢庬椶偁傞(P43)
偙偺庼嬈偺悽奅偱偺庢傝寛傔
巐暘埵偼摿偵巜掕偟側偄尷傝tukey偺僸儞僕偱
http://medbb.exblog.jp/12047409/
庼嬈偱梡偄偨悢抣乮偩傫偛乯偼埲壓偺偲偍傝
巐暘埵斖埻
IQR(interquartile range)IQR=Q3-Q1
巐暘埵曃嵎
QD(Quartile Deviation)QD=IQR/2
斖埻偼廤抍傪奜偐傜尒偨僶儔僣僉傪僀儊乕僕
曃嵎偼廤抍偺撪晹偺偁傞抣偐傜偺僶儔僣僉傪僀儊乕僕
暯嬒抣傪巊偆
mean曃嵎
Deviation傕偲傕偲偼昗弨偲側傞悢抣偐傜偺僘儗乮曃傝乯傪堄枴偡傞傕偺偩偑摑寁偺悽奅偱偼廤抍偺暯嬒抣偐傜偺僘儗傪帵偡
曃嵎偺暯嬒傪偲傟偽廤抍撪偺奺乆偺僘儗偭傉傝偑傢偐傞丂仺丂崌寁偼忢偵侽丂屘偵暯嬒傕忢偵侽
暘嶶
varianceV丂excel娭悢偼VAR
曃嵎偺擇忔偟偨傕偺偺暯嬒
昗弨曃嵎
Standard Deviation婰崋偼昗杮昗弨曃嵎s丂曣昗弨曃嵎冃
s=併V
乮屘偵V偼s^2傗冃^2偱昞尰偡傞乯
庼嬈拞愢柧偵梡偄偨昞
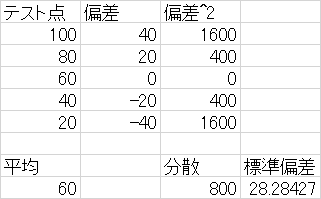
摓払搙妋擣
俀乯係偮偺広搙偵偮偄偰偦傟偧傟偺曄検偺椺傪偁偘丄摿挜傪婰偣
俁乯師偺搙悢暘晍昞偺A乣C偵擖傞悢抣傪婰偟擜検偺暯嬒抣傪奣嶼偣傛
係乯乮傑偲傔偰偍偔偙偲乯側偤丄晄曃暘嶶偱偼曃嵎暯曽榓傪n偱偼側偔n-1偱妱傞偺偐丅徹柧偣傛
| 奒媺 | 奒媺抣 | 搙悢 | 憡懳搙悢 | 椵愊搙悢 | 椵愊憡懳搙悢 |
|---|---|---|---|---|---|
| 0.5乣1.0 | |||||
| 1.0乣1.5 | 6 | A | 0.325 | ||
| 1.5乣2.0 | 0.1 | 17 | |||
| 2.0乣2.5 | B | 0.65 | |||
| 2.5乣3.0 | 7 | ||||
| 3.0乣3.5 | 0.125 | C | |||
| 3.5乣4.0 | |||||
| 寁 | ----- | 1.00 | ----- | ----- |
曗懌
|
嫵壢彂奩摉儁乕僕 戞2復乮P22-33,P43乯 暘嶶偺偲偙傠偪傚偭偲惍棟偟偰偍偒傑偟傚偆丅 嫵壢彂偱偼昗杮昗弨曃嵎傪晄曃暘嶶偵傛傞傕偺偲偟偰偄傞偺偱 乮幚梡忋偦傟偱傛偄偑丄崿棎偟側偄傛偆偵惍棟乯 曣暘嶶 冃^2丗曣廤抍偺暘嶶丒丒丒慡梫慺偺抣偑昁梫 昗杮暘嶶 倱^2丗昗杮偺暘嶶丒丒丒昗杮偺抣偑昁梫 晄曃暘嶶 倳^2丗昗杮傛傝曣暘嶶偺晄曃悇掕検傪傕偲傔偨傕偺 亙嶲峫亜昗杮暯嬒, 昗杮暘嶶, 晄曃暘嶶乮棶媴戝妛岺妛晹揹婥揹巕岺妛壢揹巕僔僗僥儉岺妛島嵗(弝嫵庼)敿毰 帬乯 http://dsl4.eee.u-ryukyu.ac.jp/DOCS/error/node19.html 昗杮暘嶶偲晄曃暘嶶傕偳偪傜傕曣暘嶶偺悇掕抣丒暯嬒抣偺悇掕偲偼儚働偑堘偆 忋婰僒僀僩偐傜堷梡乽惓婯暘晍偵懳偟, 昗杮暯嬒偼暯嬒偺嵟栟悇掕検偐偮晄曃悇掕検側偺偱偁傞偑, 昗杮暘嶶偼暘嶶偺嵟栟悇掕検偱偼偁傞偑晄曃悇掕検偱偼側偔, 晄曃暘嶶偼暘嶶偺晄曃悇掕検偱偼偁傞偑嵟栟悇掕検偱偼側偄丅 乿 |
戞4夞丂暯嬒抣偺悇掕
摓払栚昗係亅侾昗弨曃嵎偲昗弨岆嵎偺堘偄傪愢柧偱偒傞
係亅俀曣暘嶶偑枹抦偺応崌偱傕曣暯嬒傪嬫娫悇掕偱偒傞
悇掕
曣廤抍偐傜拪弌偟偨昗杮傪婎偵曣廤抍偺暘晍傪帵偡抣乮曣悢乯傪悇應偡傞揰悇掕偲嬫娫悇掕偑偁傞
揰悇掕
堦偮偺抣偱悇掕曣暯嬒偺悇掕抣偼昗杮暯嬒
曣暘嶶偺悇掕抣偼晄曃暘嶶
嬫娫悇掕
曣悢偑偁傞妋棪偱擖傞暆傪帩偭偨悇掕抣P25偺傛偆偵丄曣暯嬒偼堦掕偩偑昗杮暯嬒偼昗杮枅偵堎側傞
昗杮暯嬒偵暆傪帩偨偣傞偙偲偱丄偦偺榞撪偵曣暯嬒偑擖傞
惓婯暘晍
嵍塃懳徧偺掁忇忬暘晍乮嫵壢彂P34乯暯嬒抣偵嬤偄傎偳弌尰棪偑崅偔墦偞偐傞偵廬偭偰掅偔側傞乮偙偲偑懡偄乯
摨偠儌僲傪摨偠忦審偱孞傝曉偡偲惓婯暘晍偲偄偆榖
恀搙偲惛搙偺榖乮岆嵎乯偵抲姺偊傞偲

忋抜偑惓婯暘晍丅悶峀偑傝偑塃偵峴偔傎偳峀偑傞
壓偺抜偼椙偔傢偐傜側偄暘晍偵側傞偑丄椺偊偽P35偺傛偆側崿惉暘晍偺応崌傕偁傝偆傞
倠丂怣棅嬫娫尷奅巜悢丒丒丒昗弨惓婯暘晍偱z僗僐傾偺偙偲
昗弨惓婯暘晍
暯嬒抣偑侽昗弨曃嵎亖侾乮暘嶶傕侾乯偵側傞傛偆偵抣傪曄姺偟偨傕偺
曃嵎抣偼暯嬒抣傪50丄昗弨曃嵎亖侾侽偵側傞傛偆偵抣傪曄姺偟偨傕偺
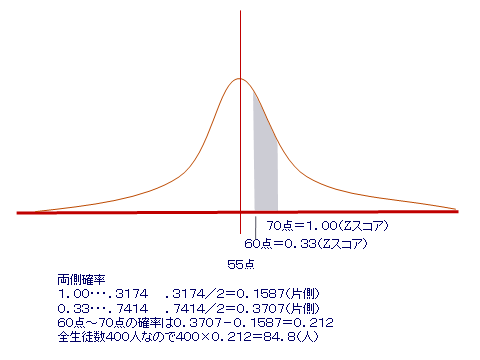
P41椺戣4傪偟偰傒偰偔偩偝偄丅乮係乯偲偟偰60揰乣70揰偵娷傑傟傞妛惗偼壗恖丠
夞摎椺
拞怱嬌尷掕棟
昗杮偺戝偒偝偑廫暘偱偁傟偽昗杮暯嬒偺暘晍偼惓婯暘晍丂仺惓偟偔應掕偝傟偰偄傞偺偱偁傟偽嬼慠岆嵎偺敪惗偼惓婯暘晍偵廬偆
丂仺應掕夞悢傪憹傗偣偽憹傗偡傎偳
亙嶲峫亜 http://aoki2.si.gunma-u.ac.jp/lecture/SampleSurvey/samplesize.html
昗弨曃嵎偲昗弨岆嵎
乮嫵壢彂P52乯丒昗弨曃嵎偼昗杮偺暘晍偺僶儔僣僉嬶崌傪帵偟偨傕偺
丒昗弨岆嵎偼曣廤抍偐傜拪弌偟偨昗杮偺暯嬒抣偺僶儔僣僉嬶崌
SE=冃乛併n
P89偺榖偼岆嵎揱斃偺朄懃偺榖
巹偑夁嫀偵棟桼傪愢柧偟偨偲偒偺帒椏 http://www.medbb.net/education/ocrstat2015/index.html
曣昗弨曃嵎偑枹抦偺応崌偺嬫娫悇掕
P63-69 惓婯暘晍偼曣暯嬒抣偲曣昗弨曃嵎偑暘偐傜側偄偲巊偊側偄仺n偑懡偄応崌昗杮暯嬒偲昗杮昗弨曃嵎偱嬤帡偱偒傞偑n偑彮側偄応崌偼嬤帡偱偒側偄仺t暘晍(昗杮偺帺桼搙兯偝偊傢偐偭偰偄傟偽丄屻偼専掕摑寁検傪媮傔傟偽妋棪偑傢偐傞)
倲暘晍
P63
帺桼搙偺傒偱偒傑傞妋棪暘晍
帺桼搙丒丒丒昗杮偺拞偱帺桼偵怳傞晳偆偙偲偑嫋偝傟偰偄傞屄懱偺悢
丂丂丂丂丂丂摑寁抣偑曣悢偺悇掕偲側傞偲丄帺桼偵怳傞晳偊側偄屄懱偑弌偰偔傞乮偮偠偮傑崌傢偣乯
昗杮暘嶶偼曃嵎擇忔榓傪屄懱偺悢偱彍偡傞偙偲偱媮傔傞偑曣暘嶶偺傎偳傛偄悇掕偱偁傞晄曃暘嶶偼n-1乮帺桼搙乯偱彍偡傞
曣昗弨曃嵎偑枹抦偺応崌偲婛抦偺応崌傑偲傔
P69
摓払搙妋擣
侾乯P33墘廗侾偺僨乕僞傪梡偄偰偦偺恖偺曣暯嬒懱廳偺95%怣棅嬫娫傪媮傔傛俀乯P68椺戣9偺95%怣棅嬫娫傪亇0.2埲撪偵梷偊傞偵偼旐尡幰偼壗柤埲忋昁梫偐媮傔傛
俁乯乮傑偲傔偰偍偔偙偲乯側偤丄昗弨岆嵎偼昗弨曃嵎s傪應掕夞悢偺惓偺暯曽崻併n偱妱傞偺偐
曗懌
|
嫵壢彂奩摉儁乕僕 戞2復乮P25,33,35-41乯 戞3復乮P52-53乯 戞4復乮P63-69乯 摓払搙妋擣偺摎偊 侾乯 P242傛傝 暯嬒抣亖53.3kg 晄曃暘嶶=0.363 晄曃昗弨曃嵎=0.602kg t兛=2.447 怣棅嬫娫[53.3-2.447*0.602/sqrt(7),53.3+2.447*0.602/sqrt(7)] [52.7,53.9] 俀乯 t兛傪屌掕偡傞傋偒偐壜曄偡傋偒偐偱榖偑彮偟曄傢傞偑 屌掕偺応崌丂(2.030*1.1/0.2)^2=124.6 125恖埲忋 t兛=1.96偲偡傞偲(1.96*1.1/0.2)^2=116.2 117恖埲忋 僉僢僠儕寁嶼偡傞偲(1.981*1.1/ 栤戣偺傑傑偱偁傟偽晄曃暘嶶傪媮傔偨偲偒偺怣棅嬫娫尷奅巜悢偱悇掕偡傞偺偑懨摉丂仺丂125恖埲忋偲偡傞丅 乮偲傕偐偔0.2埲撪偵梷偊傞偙偲傪峫偊傞偲丄崅偔側傞忦審偱媮傔傞傋偒偱怣棅嬫娫尷奅巜悢偑崅偔側傞忦審偱偁傞偙偲偲丄晄曃暘嶶傕僒儞僾儖偑憹偊偨偲偒偵彫偝偔側傞偙偲偑婜懸(n-1佮n偲側傞)偝傟傞偺偱乯丒丒丒扐偟摿偵巜帵偑柍偄偺偱嶼弌崻嫆傪帵偣偽椙偄 堦晹偺妛惗偝傫偲丄侾乯偺夞摎偑惓婯暘晍傪巊偭偰偄傞働乕僗偑懡偐偭偨榖傪偟偰偄偨偺偱偡偑丄偦偙偐傜曗惓懳徾栤戣偺榖傪偟傑偟偨丅僱僢僩忋偱偼堛巘崙壠帋尡偵娭偡傞偲偙傠偼尒偁偨傝傑偣傫偱偟偨丅 栻嵻巘崙壠帋尡偺傕偺偼埲壓乮m3.com乯 https://www.m3.com/news/iryoishin/310654 |
戞5夞丂婰弎摑寁乮嘩乯亅憡娭學悢丒夞婣捈慄
摓払栚昗俆亅侾憡娭學悢傪愢柧丒寁嶼偡傞偙偲偑弌棃傞
俆亅俀夞婣捈慄偑偳偺傛偆側傕偺偐愢柧偡傞偙偲偑弌棃傞
憡娭
乮嫵壢彂P19乯 correlative憡娭娭學偑偁傞丒丒丒娭楢偑偁傞
憡娭娭學偑柍偄丒丒丒娭楢偑側偄
懠曽偺塭嬁傪庴偗傞偐庴偗側偄偐
場壥
cause and effect尨場偲寢壥
場壥娭學偑偁傞丒丒丒塭嬁偑偁傞
場壥娭學偑柍偄丒丒丒塭嬁偑側偄
晛捠偼娭楢偑偁傞乮憡娭偑偁傞乯亖塭嬁傪媦傏偡娭學乮場壥娭學偑偁傞乯偲峫偊傞乮峫偊偨偔側傞乯
椺
偨偽偙傪媧偆亅攛偑傫丒丒丒丒憡娭娭學仜
僞僶僐傪媧偆恖偵僐乕僸乕傪堸傓恖偑懡偄偺偼丒丒丒乮yahoo抦宐戃乯
http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1293675642
偙偺娭學傪巊偆偲
僐乕僸乕傪堸傓亅攛偑傫丒丒丒憡娭娭學仜
僐乕僸乕垽堸幰偵攛偑傫偑懡偄棟桼偼丠惗妶廗姷偲偺娭楢傪専徹
傾儊儕僇偱栺50枩恖傪懳徾偵偟偨挷嵏偐傜
from International journal of epidemiology
http://medley.life/news/item/5589521b660815fe00d5ec8e
僐乕僸乕偲攛偑傫偺憡娭娭學偵妱傝崬傫偱偄傞乮偳偪傜偲傕憡娭娭學偑偁傞乯忬懺亖岎棈)
妱傝崬傫偱偄傞偦傟亖岎棈場巕丒丒丒偨偽偙
僐乕僸乕偲攛偑傫偵場壥娭學偑柍偄偲偟偨側傜偦偺娭學偼媈帡憡娭
椺丗揹幵偵忔傞偲偒奆偑偦傟偧傟墂偵岦偐偭偰拠椙偔曕偄偰傞傛偆偵尒偊傞偑丄屳偄偵娭學偼柍偄丅
夝愢偼嫵壢彂P191
杮庼嬈乮摑寁妛乯偼堛椕宯懳徾偱乽採嫙偡傞堛椕偑媦傏偡塭嬁傗偦偺梫場偵娭偡傞朄懃惈傪尒偄偩偡曽朄傪扵媮偡傞妛栤暘栰乿乮嵞宖乯
抦傝偨偄偺偼乽塭嬁乿偱偁傞偐傜栚揑傪尒幐傢側偄傛偆偵
憡娭恾
X幉偲Y幉偵堦偮偺懳徾偵梌偊傜傟傞偦傟偧傟偺抣傪僾儘僢僩乮椺丗恎挿偲懱廳乯偲傝偁偊偢恾偵偡傞偲娭學偑捈姶揑偵傢偐傞乮応崌偑偁傞仺岎棈尰徾岎屳嶌梡偵拲堄乯
憡娭學悢
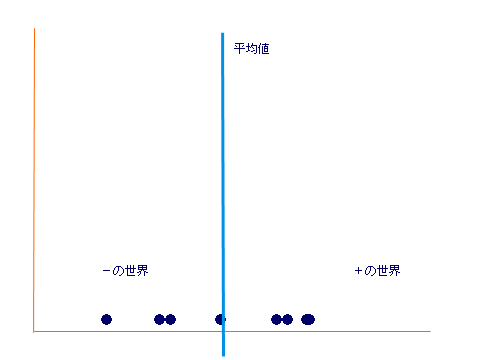
-1偐傜1傑偱偺抣傪偲傞乮嫵壢彂P163乯亄偺応崌惓偺憡娭丂亅偺応崌晧偺憡娭
X偑憹壛偡傟偽Y傕憹壛偡傞丒丒丒1
X偑憹壛偡傟偽Y偼尭彮偡傞丒丒丒-1
X偑憹壛偟傛偆偑尭彮偟傛偆偑Y偼娭學側偄丒丒丒0
憡娭學悢偑0弌側偗傟偽憡娭偼乽偁傞乿儚働偩偑掱搙偼悢帤偑0偐傜棧傟傞傎偳嫮偔側傞
堦斒偵乣0.2偱偁傟偽憡娭偼側偔丄0.7乣偱偁傟偽嫮偄憡娭偺栚埨偲偝傟偰傞丅
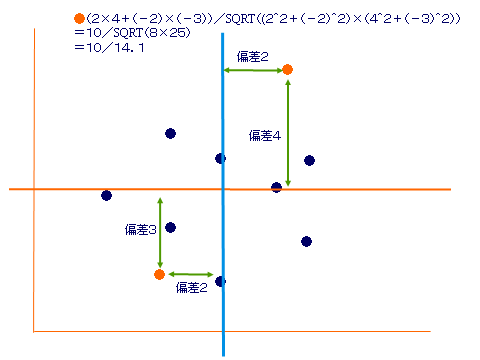
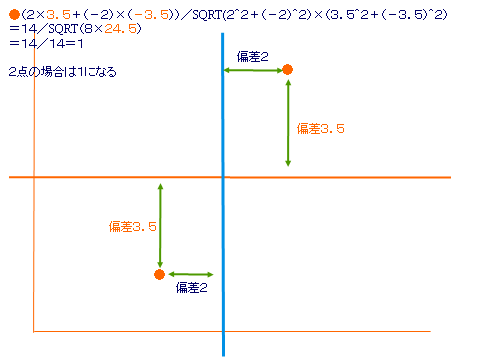
X幉偱尒偨偲偒偺僶儔僣僉嬶崌偲Y幉偱尒偨偲偒偺僶儔僣僉嬶崌傪尦偵寁嶼偟偰傞
僶儔僣僉亖嶶晍搙丒丒丒暘嶶丒丒丒曃嵎偺擇忔偺暯嬒
嫟暘嶶亖偁傞懳徾偺X幉偺曃嵎偲Y幉偺曃嵎傪忔偠偨傕偺偑儀乕僗
拲堄
婎杮帠崁偺偲偙傠偼曃嵎暯曽榓偺榖偵側偭偰偄傞偑昗杮暘嶶偺応崌椉曈傪n偱妱傜側偄偲偄偗側偄
妱傞偲丒丒丒擇忔偺暯嬒亅暯嬒偺擇忔丂偲偄偆儕僘儉姶偺偁傞岞幃偑弌棃傞
丂丂
| X偺曃嵎 | Y偺曃嵎 | 忔偠偨寢壥 |
|---|---|---|
| 亄 | 亄 | 亄 |
| 亄 | 亅 | 亅 |
| 亅 | 亄 | 亅 |
| 亅 | 亅 | 亄 |
嫟暘嶶偼X幉Y幉偺僶儔僣僉嬶崌偑崿偞偭偰偄傞偺偱偦偺傑傑偺悢帤偩偲夝庍偟偵偔偄仺X偲Y偺昗弨曃嵎偱彍偡傞乮惓婯壔乯仺憡娭學悢
愢柧偡傞偲乮僋儕僢僋偡傞偲暿僂僀儞僪僂棫偪忋偑傝傑偡乯

捈慄偱柍偄応崌偼曄悢曄姺乮椺偊偽懳悢曄姺乯偟偰偐傜寁嶼偟偰傕傛偄乮懳悢僌儔僼乯
懳悢僌儔僼偺椺乮曽娽巻僱僢僩乯
http://houganshi.net/taisuu.php
夞婣捈慄
X幉偺抣偲Y幉偺抣傪悢幃乮y=ax+b乯偱帵偡捈慄傪堷偄偨偲偒偵偦傟偧傟偺揰偐傜偺嵎乮巆嵎乯偺2忔偟偰懌偟偨傕偺乮暯曽榓乯偑嵟傕彫偝偄帪偺悢幃偑夞婣捈慄
寛掕學悢
憡娭學悢傪擇忔偡傞偲媮傔傜傟傞悢幃偵傛偭偰愢柧偱偒傞妱崌傪帵偡丅乮婑梌棪偲傕乯
偮傑傝崅偗傟偽崅偄傎偳悢幃偱愢柧弌棃傞偙偲偵側傞
僨儌乮P169椺戣33乯曗懌
曄悢偺掕媊撈棫曄悢丒丒丒input乮僐儞僩儘乕儖弌棃傞乯
廬懏曄悢丒丒丒output乮宯偵傛偭偰寛傑傞乯
桳堄嵎偺榖偼丄戞8夞丂専掕偺尨棟
偱愢柧偡傞梊掕偱偡偺偱丄崱夞偺偲偙傠偼僗儖乕偟傑偡
乮嫵壢彂P171r昞偺榖側偳偼偦偺帪偵乯
摓払搙妋擣
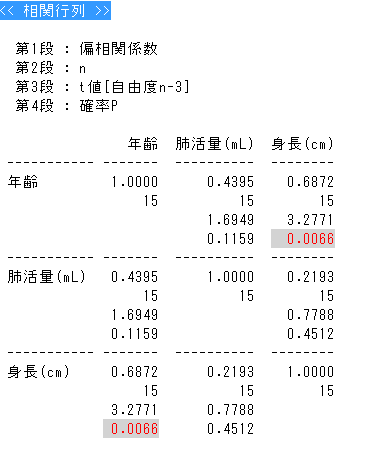
侾乯P188椺戣38偺僨乕僞傛傝憡娭學悢傪媮傔傛俀乯師偺昞偵帵偡4慻偺僨乕僞偺憡娭學悢倰亖-1偩偭偨丅A丂B丂偵擖傞悢抣傪婰偣
| ID | x | y |
|---|---|---|
| 1 | 4.5 | 1.2 |
| 2 | -1 | A |
| 3 | B | 4 |
| 4 | 8.5 | 0.6 |
曗懌
|
嫵壢彂奩摉儁乕僕 戞1復乮P19乯 戞9復乮P162-170,181-188乯 戞10復乮PP191-192乯 摓払搙妋擣偺摎偊 侾乯 r=Sxy/sqrt(Sxx亊Sxy)偵壓婰偺抣傪戙擖 Sxx=64.85 Syy=66.35 Sxy=62.85 r=62.85/sqrt(64.85*66.35)=0.958 媽朄偲怴朄偺榖偱偡偐傜憡娭學悢掅偄偲偦偺傑傑戙懼偡傞偵偼栤戣偱偁傝傑偡丅 P164偺曽朄偱峴偆応崌偙偙偱弌偰偄傞昗弨曃嵎偲偼晄曃昗弨曃嵎乮曣廤抍偺悇掕乯側偺偱乮n-1偱妱偭偰偄傞乯拲堄偺偙偲 偙偺嫵壢彂偱偼昗杮暘嶶傪晄曃暘嶶偲偟偰偄傞偨傔曃嵎暯曽榓偵傛傞寁嶼幃偵偟偰偄傞 俀乯 ID1媦傃4傛傝 y=-0.15x+1.875 A=-0.15*(-1)+1.875=2.025 4=-0.15B+1.875 亪B=(4-1.875)/(-0.15)=-14.167 傕偆彮偟僉儕椙偔摎偊弌偣傞梊掕偱偟偨偑丒丒丒 俀乯偺栤戣偺傛偆側憡娭學悢抣偁傝偒偺榖偼捠忢桳傝摼側偄丅棟夝偺偨傔栤戣偵偟傑偟偨 |
戞6夞丂姶搙丒摿堎搙丒ROC嬋慄
摓払栚昗俇亅侾敾暿摿惈抣偺寁嶼偑弌棃傞
俇亅俀昡壙寢壥傛傝ROC嬋慄傪嶌惉偟昡壙傗僇僢僩僆僼抣偺専摙偑弌棃傞
専嵏朄偺恌抐揑桳梡惈傪昡壙偡傞榖
桳昦棪偺塭嬁傪庴偗傞巜昗丄庴偗側偄巜昗傪惍棟偟偰偍偔偙偲
姶搙偲摿堎搙
嫵壢彂乮P104乯姶搙亖P(梲惈|俢) 丂幘姵孮偵偍偗傞恀梲惈偺妱崌
婾梲惈棪亖P(梲惈|俢c) 旕幘姵孮偵偍偗傞婾梲惈偺妱崌
摿堎搙亖侾亅婾梲惈棪 旕幘姵孮偵偍偗傞恀堿惈偺妱崌
梊應抣
丂梲惈揑拞棪亖P(俢|梲惈)
丂堿惈揑拞棪亖P(俢c|堿惈)
専嵏朄偺昡壙巜昗
丂栟搙斾亖姶搙/婾梲惈棪丂
丂僆僢僘斾亖嫵壢彂嶲徠丂専嵏偺桳梡惈
丂ROC亅AUC亖ROC嬋慄傪昤偄偰嶼弌丂専嵏偺暘暿擻
壗偱傕梲惈偲敾抐偡傞専嵏偼姶搙傕婾梲惈棪傕侾偵側傞
乮側傫偱傕偐傫偱傕丄偁傝傑偡!両丂偺僲儕乯
ROC嬋慄
嫵壢彂乮P107乯敾暿搙偺暘愅
姶搙偲婾梲惈棪乮侾亅摿堎搙乯傪梡偄偰嬋慄傪昤偔
椺戣20偱嘐傪僇僢僩僆僼抣偲偟偨偲偒偺姶搙丒摿堎搙丒梲惈揑拞棪丒堿惈揑拞棪傪媮傔偰傒偰偔偩偝偄
庼嬈偱偼儅儞儌僌儔僼傿偺椺傪徯夘偡傞偺偱埲壓徯夘偟偰偍偒傑偡
嶲峫丗儅儞儌僌儔僼傿媄弍曇乮堛椕壢妛幮乯偺尒杮
http://www.iryokagaku.co.jp/frame/03-honwosagasu/391/index03-391.html
摓払搙妋擣
侾乯側偤梊應抣乮椺偊偽梲惈揑拞棪乯偼桳昦棪偺塭嬁傪庴偗丄姶搙偼塭嬁傪庴偗側偄偐娙寜偵弎傋傛俀乯P108椺20偺AUC傪媮傔傛乮僉僢僠儕寁嶼弌棃傑偡乯
俁乯師偺儅儞儌僌儔僼傿偺専嵏寢壥偐傜ROC嬋慄傪昤偒丄AUC傪乮彫悢揰埲壓2寘傑偱媮傔巐幪屲擖乯媮傔傛丅傑偨僇僢僩僆僼抣傪専摙偣傛
| 堎忢側偟乮侾乯 | 椙惈乮俀乯 | 埆惈傪斲掕偱偒側偄乮俁乯 | 埆惈偺媈偄乮係乯 | 埆惈乮俆乯 | 寁 | |
|---|---|---|---|---|---|---|
| 幘姵孮 | 1 | 1 | 6 | 14 | 18 | 40 |
| 旕幘姵孮 | 5 | 14 | 15 | 6 | 0 | 40 |
曗懌
|
嫵壢彂奩摉儁乕僕 戞6復乮P104-111乯 惈擻昡壙偺榖傪帺摦幵偺僄儞僕儞偱峫偊傞偲棟夝偟傗偡偄(偲彑庤偵巚偭偰偄傑偡) 攏椡偑偁偭偰傕忢梡夞揮堟偺晹暘偑僗僇僗僇乮僺乕僉乕乯偩偲埖偄偵偔偄側偳側偳 摓払搙妋擣偺摎偊 俀乯侽丏俉俆 俁乯侽丏俉俉 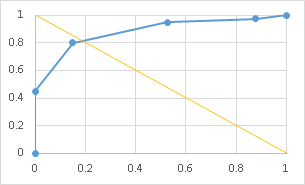 僇僢僩僆僼抣偺栚埨偼俀偲俁偺娫乮1-摿堎搙乮婾梲惈棪乯傗姶搙偺悢抣傪彂偐傟偰傕崲傞偺偱拲堄乯 専嵏偱偺僇僢僩僆僼抣偺堄枴崌偄偺榖偲擖帋偺僇僢僩僆僼抣偺榖丅屻幰偼擖妛偟偨帪揰偐傜僗僞乕僩側傢偗偱丄偦傟偼嫵堢偑愗傝奐偔枹棃偺榖偱傕偁傞丅 懖嬈帪偵擖妛偟偰椙偐偭偨偲側傞傛偆偵丄奆偝傫傕巹傕娷傔偨娭學奺埵壗懖傛傠偟偔偍婅偄偄偨偟傑偡丅 妛惗偐傜偺幙栤媦傃摓払搙妋擣偺夞摎 幙栤 Q1乯姶搙偑崅偄専嵏偱堿惈偱偁傟偽幘姵偱偁傞壜擻惈偑掅偄丂偲夝庍弌棃傞棟桼 Q2乯摿堎搙偑崅偄専嵏偱梲惈偱偁傟偽幘姵偱偁傞壜擻惈偑崅偄丂偲夝庍弌棃傞棟桼 夞摎 A1乯 庼嬈撪梕傪巚偄晜偐傋傞偲姶搙偺榖偱堿惈偺榖偼娭學側偄傛偆偵巚偭偰偟傑偆傢偗偱丅 姶搙=a/(a+c)偑崅偄偲尵偆偙偲偼丄a偑崅抣庒偟偔偼c偑掅抣 偙偙偱弎傋偰偄傞榖偼堿惈揑拞棪偺偙偲 堿惈揑拞棪=d/(c+d)偑崅偔側傞偵偼丄c偑掅抣偺応崌 桳昦棪傪堦掕偲偟偨傜丄a+c偑堦掕側偺偱姶搙偑崅偄a偼崅抣妿偮c偼掅抣偲側傞 備偊偵堿惈揑拞棪偼崅偔側傞偲偄偆榖 A2)偼摨條偺峫偊曽偱 僇僢僩僆僼抣偺榖偱忣曬張棟媄弍宯偺帋尡偺崌奿婎弨偺榖傪偟傑偟偨偑丄偁傞嬝偐傜棪傪挷惍偟偰偄傞偲暦偄偰偄偨偺偱丄偦偺傑傑挐偭偪傖偄傑偟偨偑幚嵺偵偼揰悢偱寛傔偰偍傝傑偡丅 偍偦傜偔擄堈搙偱崌奿棪傪挷惍偟偰偄傞偲尵偆榖側偺偩偲巚偄傑偡偑丄岆夝偑側偄傛偆偵 IPA丄忣曬僙僉儏儕僥傿儅僱僕儊儞僩帋尡偲婎杮忣曬媄弍幰帋尡偺崌奿幰傪敪昞丄堎椺偺崌奿棪丄梊憐奜偺庴尡幰憌(帒奿Zine僯儏乕僗) http://shikakuzine.jp/article/detail/124 |
戞7夞丂憡懳婋尟搙
摓払栚昗俈亅侾憡懳婋尟搙傪帵偡巜昗偵偳偺傛偆側傕偺偑偁傞偐愢柧偱偒傞丂
俈亅俀徢椺懳徠尋媶偱偼憡懳婋尟傪僆僢僘斾偱嶼弌偡傞棟桼傪愢柧偱偒傞
憡娭偼娭楢偑偳偺掱搙偁傞偐
敾抐暘愅偼丄幘姵傪専嵏偵傛傝偳偺掱搙敾抐偡傞偙偲偑弌棃傞偐
憡懳婋尟搙偼丄幘姵乮寢壥乯偑敇業乮尨場乯偺塭嬁傪偳偺掱搙庴偗偰偄傞偺偐
巜昗偼悢帤偲偟偰寁嶼弌棃傞尷傝寢壥偑尰傟傞偺偩偑丄偦傟偺夝庍傪岆傜側偄傛偆偵偡傞偙偲偱偁偭偨傝丄偦傕偦傕夝庍偟傛偆偑柍偄偺偱弌偟偰傕堄枴側偟偺応崌傕偁傞
偙偺庼嬈偱偼憡懳婋尟搙=Relative Risk 偼堦斒揑側梡岅偱偁傝丄偦偺嶼弌巜昗偺堦偮偵憡懳婋尟亖儕僗僋斾乮Risk Ratio乯偑偁傞偲惍棟偟傑偡
堦斒揑偵偼偙偙傜傊傫偺尵梩僑僠儍僑僠儍偱偡丅
尋媶庤朄偺榖
乮嫵壢彂P190乯娤嶡尋媶(Observational study)
墶抐尋媶乮Cross-sectional study乯敇業偲幘姵傪摨帪偵昡壙
帪娫幉偑側偄応崌偑懡偔乮椺奜偼惈暿側偳乯場壥娭學傑偱偼晄柧偵側偭偰偟傑偄傗偡偄
僐儂乕僩尋媶乮Cohort study乯
懳徾偵敇業偟偰偄傞恖乆傪攃埇偟丄偦偺拞偐傜敇業孮偲旕敇業孮傪愝掕丄捛愓挷嵏偟偰偄偔僗僞僀儖
捠忢慜岦偒偩偑丄屻傠岦偒偵傒傞夞屭揑僐儂乕僩尋媶偲偄偆偺傕偁傞丅乮屻乆偱傕敇業孮偵娭偡傞忣曬偑偁傞応崌乯
徢椺懳徠尋媶乮Case-control study乯
偁傞忬懺乮椺偊偽昦婥偵滊姵偟偰偄傞乯孮偲丄滊姵偟偰偄側偄孮傪愝掕丄帪娫傪慿偭偰挷嵏偟偰偄偔僗僞僀儖
屻傠岦偒偵偟偐峴偊側偄乮慜岦偒偩偲敇業仺幘姵偺弴偑偍偐偟偔側傞乯
幚尡揑尋媶乮夘擖尋媶乯乮intervention study乯
僐儂乕僩尋媶偺応崌丄敇業孮乮夘擖孮乯傪尋媶幰偑妱傝晅偗傞丂仺丂旐尡幰偵懳偡傞椣棟揑攝椂偑娞梫柍嶌堊偵妱傝晅偗傞偙偲偑弌棃傞応崌偼岎棈場巕傪惂屼偱偒傞乮偙偲偑婜懸偝傟傞乯
椣棟揑偵峫偊傞偲旕夘擖孮偺曽偑晄棙塿偵側偭偰偟傑偆壜擻惈偑崅偄偺偱丄攝椂偟偨尋媶僨僓僀儞偑媮傔傜傟傞
愢柧梡僨乕僞
| 幘昦敪徢 | 幘昦柍 | 寁 | |
|---|---|---|---|
| 敇業桳 | A | B | A+B |
| 敇業柍 | C | D | C+D |
| 寁 | A+C | B+D |
憡懳婋尟
Risk Ratio(RR)乽儕僗僋斾乿偲尵偭偨曽偑傢偐傝傛偄乮偲巚偆偑乯
敇業乮夘擖乯偺桳傞帪偲柍偺帪偺婋尟傪帵偡巜昗偺斾
婋尟傪帵偡巜昗偵偼滊姵棪傗傜桳昦棪傗傜巰朣棪傗傜
A乣D:幘昦敪惗昿搙乮昿搙埲奜偵滊姵棪傗傜桳昦棪丒丒丒乯
敇業桳孮偺敪徢儕僗僋亖A/(A+B)
敇業柍孮偺敪徢儕僗僋亖C/(C+D)
儕僗僋斾亖A/(A+B)乛C/(C+D)
傕偟丄敪惗昿搙偑掅偗傟偽A+B佮B丂C+D佮D
丂儕僗僋斾佮A/B乛B/D亖AD/BC
僆僢僘斾
Odds Ratio(OR)乽儕僗僋斾乿傪弌偣側偄応崌偱傕弌偣傞乮儕僗僋斾偼偦傟偧傟偺孮偺儕僗僋偑傢偐偭偰偄側偄偲弌偣側偄乯
婋尟側帠徾偑婲偒偨応崌偲婲偒側偐偭偨応崌搙悢偺斾乮亖僆僢僘乯偵偮偄偰敇業乮夘擖乯偺桳柍枅偵媮傔斾傪偲偭偨傕偺
敪徢桳孮偺敇業僆僢僘亖A/C
敪徢柍孮偺敇業僆僢僘亖B/D
僆僢僘斾亖A/C乛B/D
丂丂丂丂亖AD/BC
忋婰偺傛偆偵敪徢昿搙偑掅偗傟偽僆僢僘斾偲儕僗僋斾偺嬤帡抣偲側傞
摓払搙妋擣
僐儂乕僩偲徢椺懳徠尋媶椉曽偱峴偭偰偄偨傕偺偲偡傞丅侾乯偦傟偧傟偐傜憡懳婋尟搙乮儕僗僋斾傕偟偔偼僆僢僘斾乯傪媮傔傛
俀乯儕僗僋斾偲僆僢僘斾偼嬤帡抣偲側傞忦審傪弎傋傛
俁乯徢椺懳徠尋媶偱偼側偤儕僗僋斾傪媮傔偰偨傜偩傔側偺偐丅娙寜偵弎傋傛
係乯夘擖尋媶偱偼椣棟揑側栤戣偵拲堄偟側偔偰偼側傜側偄偑僫僛偐丠帺暘偺峫偊傪娙寜偵弎傋傛
僐儂乕僩尋媶
| 晄惍柆偁傝 | 晄惍柆側偟 | 寁 | |
|---|---|---|---|
| 敇業孮 | 100 | 1900 | 2000 |
| 旕敇業孮 | 50 | 1950 | 2000 |
| 寁 | 150 | 3850 | 4000 |
| 晄惍柆偁傝 | 晄惍柆柍偟 | 寁 | |
|---|---|---|---|
| 敇業楌偁傝 | 50 | 30 | 80 |
| 敇業楌柍偟 | 50 | 70 | 120 |
| 寁 | 100 | 100 |
曗懌
|
嫵壢彂奩摉儁乕僕 戞10復乮P190-194乯 徯夘偟偨摦夋乮NATS嶌惉旘峴婡偺壜帇壔乯 http://videotopics.yahoo.co.jp/videolist/official/others/p2fa7e9e1ddcf091a4586fb2068d46390 |
戞8夞丂専掕偺尨棟
摓払栚昗俉亅侾妋棪偑偳偺傛偆側堄枴崌偄偺傕偺偐棟夝偡傞
俉亅俀壖愢専掕偺榑棟峔惉傪愢柧偱偒傞
嫵壢彂戞嶰復P48乣
妋棪
偁傞帠徾偑婲偙傞偙偲偑婜懸偝傟傞搙崌偄乮妱崌乯偁傞屄懱偵帠徾偑婲偙傞乛婲偙傜側偄偺偄偢傟偐偲偟偰傕丄妋棪偱偼摎偊傜傟側偄
帋峴丂僒僀僐儘傪怳偭偰俁偺栚偑弌傞(y or n)
妋棪丂僒僀僐儘傪怳偭偰俁偺栚偑弌傞(1/6)
孞傝曉偟帋峴傪峴偆偲昿搙妱崌偼偦偺帠徾偺妋棪傊廂懇偟偰偄偔
惗暔傪懳徾偲偟偨応崌帋峴傪孞傝曉偣傞丠仺柍棟側応崌偑懡偄仺忦審傪嬤偯偗偰孞傝曉偟偨偲尒橍偡
婣擺乮屄暿偺帠徾偐傜朄懃傪摫偒弌偡乯佁墘銏
嶲峫
悇榑偺婎杮乽墘銏朄乿偲乽婣擺朄乿傪巊偄暘偗偰峫偊傞椡傪恎偵偮偗傛偆
http://matome.naver.jp/odai/2139625697364840601
偟偐偟帋峴偺寢壥偼帠幚偲偟偰惓偟偄偑丄偐偲偄偭偰偦傟偑妋棪揑偵惓偟偄乮恀乯偲偼尷傜側偄
師偺帋峴埲崀偱堎側傞寢壥偑偱傞壜擻惈傪攔彍偱偒側偄仺塱墦偵帋峴傪孞傝曉偝側偄偲側傜偢朄懃偑弌偣側偄
乮屘偵堎側傞尰徾偺婲偙傞妋棪偵偨偄偟偰鑷抣傪掕傔偰丄側偐偭偨偙偲偵偟偰堦斒惈傪庡挘偡傞僗僞僀儖乯
帠徾偺婲偙傞妋棪偑挊偟偔掅偔偰傕丄幚嵺偵婲偙傜側偄傢偗偱偼側偄丅
嶲峫
傑偝偵楌巎揑弖娫丄僆僶儅戝摑椞偺旐敋抧僸儘僔儅朘栤偵偝偡偑偺僥儗價搶嫗傕摿暿斣慻偱惗拞宲
http://kabumatome.doorblog.jp/archives/65863513.html
攚棟朄
柦戣偺斲掕傪壖掕偟偰榖傪偡偡傔傞偙偲偱柕弬傪帵偡偙偲偱柦戣偑惉傝棫偮偲偡傞榑朄壖愢専掕
嫵壢彂P48-亙戝慜採亜傗傒偔傕偵専掕偡傞偺偱偼側偔丄専掕偡傞棟桼丒妋怣偑偁傞偐傜妋偐傔傞丂偲偄偆姶偠偱
庤弴侾丗壖愢傪偨偰傞乮婣柍壖愢H0偍傛傃懳棫壖愢H1乯
攚棟朄偵婎偯偔徹柧傪偟偰偄傞丅
乮嵎偑側偄壖愢偑徹柧偱偒側偄偺偱丄偦偺懳棫偱偁傞嵎偑偁傞壖愢傪嵦戰偡傞乯
庤弴俀丗桳堄悈弨傪寛傔傞
妋棪揑偵昁慠偲嬼慠傪愗傝暘偗偰偄傞丅堦斒偵俆亾偱暘偗偰偄傞偑侾亾偺帪傕偁傞
庤弴俁丗専掕摑寁検傪寁嶼偡傞
偦偺帠徾偺婲偙傞妋棪傪寁嶼偟偰偄傞偙偲偵側傞偑丄梡偄傞妋棪暘晍偵傛偭偰寁嶼幃偑堎側傞丅
庤弴係丗桳堄悈弨偲斾妑偟丄壖愢傪婞媝嵦戰偡傞
椺乯婣柍壖愢H0傪婞媝偟懳棫壖愢H1嵦戰
拲堄
嬫娫悇掕偺榖偺墑挿慄忋偑専掕乮P69偲P50傪斾妑乯
攝晍帒椏偺夝愢
壖愢専掕偑偟偭偔傝偟側偄偦傕偦傕
乽偁傞乿偺斀懳偑乽側偄乿偭偰偺偼堘偆傫偠傖側偄偺乮壗偑偁傞偺丠側偄偺丠乯
懳棫壖愢乮偁傞乯偺斲掕偼婣柍壖愢乮側偟乯偱偼乮側偟乯偺斀懳偼擇廳斲掕偵側傞偵偼丂仺丂壖愢偺棫偰曽
乽娭怱偑偁傞乿偺斀懳偼乽娭怱偑側偄乿丅偩偐傜乽岲偒乿偺斀懳偼乽娭怱偑側偄乿偦偟偰乽寵偄乿偺斀懳傕乽娭怱偑側偄乿
晄姰慡側婣擺朄偱摫偔偺偭偰婋尟偠傖側偄偺
僄儔乕傪婲偙偡偙偲偑慜採偺婣擺朄乮偲傝偁偊偢寢榑傪憗偔弌偣傞傕偺偺乯兛僄儔乕丂兝僄儔乕偑懚嵼偡傞
僄儔乕傪婥偵偟側偗傟偽偄偮偺擔偐丄搒崌偺椙偄寢榑偑摼傜傟傞偐傕偟傟側偄
屘偵傗傒偔傕偵専掕偡傞偺偱偼側偔丄帄傞傑偱偺僗僩乕儕乕偑戝愗
暔岅慡懱偼墘銏朄偺榖丅専徹傪壖愢専掕巊偭偰偄傞偲棟夝偡傟偽傛偄
僨乕僞儅僀僯儞僌偺悽奅偼婣擺朄乮壖愢偼惗惉偱偒傞乯
偟偭偔傝偡傞億僀儞僩偼彑庤偵奼戝夝庍偟側偄偙偲偱丄壖愢専掕偼梡朄傪庣傝惓偟偔巊偄傑偟傚偆
僄儔乕
嫵壢彂P202戞堦庬偺夁岆乮兛僄儔乕乯丒丒丒岆偭偰堘偆偲敾掕偡傞妋棪
戞擇庬偺夁岆乮兝僄儔乕乯丒丒丒岆偭偰堦弿偲敾掕偡傞妋棪
亙嶲峫亜
惓偟偔乽摨偠乿偲敾掕偡傞妋棪丒丒丒侾亅兛
惓偟偔乽堘偆乿偲敾掕偡傞妋棪丒丒丒侾亅兝
娭楢偡傞榖
P204,198,207
桳堄嵎専掕偺桳堄悈弨偼0.05偱傛偄偺
兝僄儔乕偼0.2乮僨乕僞悢偺愝掕乯
専掕夞悢偑懡偄偲曗惓偑昁梫側棟桼
摓払搙妋擣
侾乯P50椺戣俇偺昗弨曃嵎傪偦傟偧傟俁丆俆丆俈cm僋儔僗偺恖悢傪16,25,49恖偲偟偨偲偒偵丄偦傟偧傟慡崙暯嬒偲斾傋偨偲偒慡崙悈弨偲堘偆偲尵偊傞偐丅桳堄悈弨偼1%媦傃5%偲偡傞 乮彂偒曽乯n.s. 旕桳堄 *:P亙0.05 **:P亙0.01丂
俀乯懡孮娫傪専掕偡傞嵺偵拲堄偟側偔偰偼側傜側偄偺偼偳偺傛偆側偙偲偐丠棟桼傕娷傔偰傑偲傔傛丅
曗懌
|
嫵壢彂奩摉儁乕僕 戞3復乮P48-54乯 戞10復乮P198-209乯 攝晅帒椏奩摉儁乕僕 怱棟妛揑尋媶偵偍偗傞摑寁揑桳堄惈専掕偺揔梡尷奅,妺惣弐帯,嶥杫妛堾戝妛恖暥妛夛婭梫79,P45-78, 2006 http://ci.nii.ac.jp/naid/110004812630 攝晍偟偨偺偼P7-14 徯夘偟偨摦夋 搶嫗墂偐傜慡崙奺抧傊偺強梫帪娫傪壜帇壔偟偨塮憸丅偙傟偼僞儊偵側傞両亅whats http://whats.be/114963 巚偭偨偙偲 堘偆帠傪徹柧偡傞偨傔偵奆偲堦弿偠傖側偄偐傜堘偆偲偄偆偺偼丄側偵傗傜徚嬌揑側榑朄偱弌傞峐偼懪偨傟傞揑側報徾傪帩偭偰偟傑偆偑丄廤抍嫵堢偺拞偱偦傟偧傟偺桪傟偨摿惈傪怢偽偡帠傪峫偊傞偺偑擄偟偄榖偱偁傞偙偲傪帵嵈偟偰偄傞傛偆偵傕巚偆 偨偩峐偑弌傞偙偲偱怴偟偄悽奅偑弌偰偔傞栿偱偁傞偐傜峐偑弌傞偙偲帺懱偼椙偄傢偗偱丄偦偺撪梕傪夝庍偡傞昁梫偑偁傝扤偟傕偑擸傫偱偄傞偲巚偄傑偡乮婣柍壖愢偲懳棫壖愢偺榖偲堦弿乯 |
戞9夞丂僷儔儊僩儕僢僋専掕
摓払栚昗俋亅侾僷儔儊僩儕僢僋専掕偺婃嫮惈robustness傪愢柧偱偒傞
俋亅俀t専掕傪峴偄敾掕偡傞偙偲偑弌棃傞
僷儔儊僩儕僢僋偲僲儞僷儔儊僩儕僢僋
嫵壢彂P46暘晍偺宍忬乮曣悢乯偵埶懚偡傞摑寁検乮暯嬒抣丂昗弨曃嵎丒丒丒検揑曄検乯
暘晍偺宍忬乮曣悢乯偵埶懚偟側偄摑寁検乮弴埵丂拞墰抣丂僷乕僙儞僩抣丒丒丒幙揑曄検乯
嫵壢彂P196
僲儞僷儔儊僩儕僢僋専掕偼検揑曄検偱傕梡偄傞偙偲偑弌棃傞偑丄兝乮戞擇庬偺夁岆乯偑忋徃偡傞乮侾亅兝乯亖専弌椡偑掅壓
僷儔儊僩儕僢僋専掕丒丒丒寁應抣偺暘晍偑惓婯暘晍偱偁傞偙偲傪壖掕
嫵壢彂P195
僨乕僞偑弌偰偐傜専掕朄傪慖戰偡傞偺偼揔愗偱偼側偄
嫵壢彂P6
崱夞偲師夞偱僥乕僽儖乮揔梡梫審偵傛傞巊偄暘偗乯偺忋俀峴傪懳徾
暘晍偺惓婯惈偵偮偄偰乽僨乕僞悢偑戝偒偔側傞偲惂栺柍偟乿丒丒丒偳偺掱搙 僷儔儊僩儕僢僋偺応崌仺寢嬊懨摉側榖偵側偭偰偟傑偆偑丄峫偊曽偲偟偰偼P199嶲徠偵峫偊傟偽椙偄 嫵壢彂偺岠壥検偵懳偡傞昁梫僨乕僞悢傪壜曄偝偣偨傕偺偑埲壓
奺孮10僨乕僞偱専掕偡傞偲10kg掱搙偲側傞偑丄偦偙傑偱懱廳偑曄壔偟偰偄傞偲側偵偐堘偆弌棃帠偑婲偙偭偰偄傞婥偑偡傞
奺孮1000僨乕僞偖傜偄偱専掕偡傞偲1kg掱搙偱桳堄側寢壥偲側傞偑丄杮摉偵堄枴偁傞偺偐婥偵側傞
暘嶶偺惂栺偺榖
1昗杮t専掕丒丒丒嬻敀
2昗杮t専掕丒丒丒俀孮偺摍暘嶶惈
嬻敀傪巹偼丄僨乕僞偺尦偑摨偠偲偙傠側偺偱栤戣偵側傜側偄偱偟傚偆丂偲夝庍偟偰偄傑偡丅
俀孮偺摍暘嶶惈偵娭偟偰偼丄偧傟傪慜採偲偟偰専掕偑惉傝棫偭偰偄傞偺偱乮埲壓偵徯夘偡傞乮僗僠儏乕僨儞僩偺乯t専掕偼
柍榑丄摍暘嶶偱偼側偄応崌偵梡偄傞専掕乮僂僃儖僠偺t専掕乯傕偁傞偺偱偡偑丄偦偪傜傪嵟弶偐傜巊偭偨曽偑椙偄偲偄偆榖傕偁傝傑偡丅
僲儞僷儔偐僷儔儊僩儕僢僋偺榖偲摨條偱偡偑丄偳偪傜偱傗傠偆偲傕桳堄嵎偑弌偰傞偖傜偄柧妋側傕偺偑棟憐偱偼偁傝傑偡偑
乮偙偙傜曈偺榖偼僲儞僷儔偺偲偙傠偱傂偭偔傞傔偰庢傝忋偘傑偡丂嫵壢彂P99乯
娭楢2孮偺嵎偺専掕
1昗杮t専掕
嫵壢彂P56P59椺戣8傪尒側偑傜
娭楢偡傞俀孮乮儁傾乯丒丒丒堦偮偺孮傪俀夞應掕偟偰偄傞
慜屻偺嵎傪尒傞
t抣乮昗弨壔偝傟偨専掕摑寁検乯丒丒丒俀孮偺儁傾偺嵎偺暯嬒傪昗弨岆嵎偱惓婯壔偟偨傕偺
婣柍壖愢偼慜屻偺嵎偑僛儘
専掕摑寁検偲桳堄悈弨兛偺t抣傪斾妑偡傞丅
桳堄悈弨侾亾偺応崌敾掕偼偳偆側傞偐丠
墘廗4偱妋擣偺偙偲
2昗杮t専掕
嫵壢彂P78乣丂P80椺戣12丂P87椺戣14偙偪傜偺応崌偼丄F専掕乮P86)偱摍暘嶶傪妋擣偟偰偐傜偺庤弴偵側傞丅
偟偐偟側偑傜丄嵎偑柍偄応崌偼婣柍壖愢傪婞媝偱偒側偐偭偨偲偄偆偙偲偱丄愊嬌揑偵嵎偑偁傞偙偲傪徹柧偱偒側偔偰僈僢僇儕偡傞傋偒傕偺偱偁傞乮敾掕曐棷乯
屘偵嫵壢彂偼峫椂偟偰乽摍暘嶶偲峫偊偰柕弬偟側偄乿偲昞尰偟偰偄傞
乮F暘晍偺榖側偳偼堦尦攝抲暘嶶暘愅偵偰乯
堦昗杮偲偺堘偄偼暘嶶偑俀庬偁傞偙偲乮堦昗杮偼儁傾偺嵎傪偲傞偺偱堦偮乯
偦偺偨傔崌惉偡傞
t抣丒丒丒偦傟偧傟偺孮偺暯嬒偺嵎傪昗弨岆嵎偱惓婯壔偟偨傕偺
丂偨偩偟丒丒暯嬒偺嵎偺昗弨岆嵎偼偦傟偧傟偺榓偵側傞偺偱丄SE=併(s1^2/n1)+併(s2^2/n2)偱丄嫵壢彂偺幃偵側傞
墘廗俆偱妋擣偺偙偲
丂
椉懁専掕偲曅懁専掕
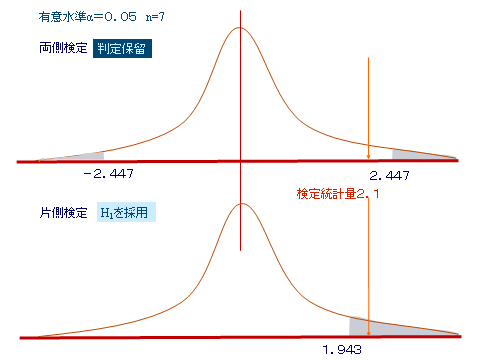
摓払搙妋擣
侾乯18恖偺姵幰偵A嵻傪1廡娫搳梌偟慜屻偺柆攺悢傪寁應偟偨丅A嵻偵岠壥偑偁傞偐専掕傪峴偆丅椉懁専掕偱桳堄悈弨兛亖0.05,0.01偱専掕偣傛丅慜敿
屻敿
俀乯A+X孮偲A孮偺峈懱壙偵桳堄嵎偑偁傞偐専掕傪峴偆丅椉懁専掕偱桳堄悈弨兛亖0.05,0.01偱専掕偣傛丅
慜敿
屻敿
曗懌
|
嫵壢彂奩摉儁乕僕 戞0復乮P5-6乯 戞2復乮P46乯 戞4復乮P56-62乯 戞5復乮P78-87乯 戞10復乮P195-199乯 攝晅帒椏奩摉儁乕僕 側偟 徯夘偟偨榖側偳 乽嬻偺F1乿偱斶婅偺弶V傪壥偨偟偨幒壆偺媡嫬恖惗乮THE PAGE乯 https://thepage.jp/detail/20160605-00000002-wordleafs 戞112夞擔杮惛恄恄宱妛夛妛弍憤夛 http://www.congre.co.jp/jspn112/ 亂岎棳愴挧敪億僗僞乕亃2016偼旕岎棳愴巑儅僕儚儔儞両僋儖乕僘傕揋儘儃僢僩偲偟偰巃傞 両乮SPIN!OUT乯 http://spinout-kj.com/poster-gandam-3460/ 巚偭偨偙偲 専掕偺榖偼丄昳幙娗棟偺榖桼棃偲峫偊傟偽椉懁専掕偑僗僞儞僟乕僪側偺偼帺柧 桳堄嵎偁傞偁傞偲巚偭偰専掕偟偰丄婣柍壖愢傪婞媝偱偒側偄帪偵偩偗丄偍偐偟偄偲巚傢側偄傛偆偵 |
戞10夞丂僲儞僷儔儊僩儕僢僋専掕
摓払栚昗侾侽亅侾僷儔儊僩儕僢僋専掕偲僲儞僷儔儊僩儕僢僋専掕偺堘偄傪愢柧偱偒傞
侾侽亅俀僲儞僷儔儊僩儕僢僋専掕傪峴偄敾掕偡傞偙偲偑弌棃傞
堦昗杮Wilcoxon専掕
僂傿儖僐僋僜儞偺晞崋晅弴埵榓専掕暘晍宆丆寁應広搙丆暘嶶偺惂栺側偟
嫵壢彂乮P6)
侾丗儁傾偺僨乕僞偺嵎d傪媮傔傞
俀丗d偺愨懳抣傛傝偦傟偧傟偺嵎乮d乯偺弴埵乮徃弴乯傪媮傔傞
俁丗専掕摑寁検T偼亄丆亅暿偵弴埵傪懌偟偨傕偺偱彫偝偄曽
桳堄妋棪偵偮偄偰偼捈愙寁嶼弌棃傞偑乮P74乯墑乆偲寁嶼偟偰偄偔偺偼戝曄
n亝25傑偱偼Wilcoxon専掕昞傪巊偭偰偔偩偝偄
n亜25偼惓婯暘晍偵嬤帡偲尒側偟偰z抣傪媮傔傞曽朄偱専掕
暯嬒抣
暯嬒抣偲側偭偰偄傞偑婜懸抣乮偨偩偟堦條側偺偱拞墰抣偱傕桳傝暯嬒抣偱傕偁傞偑乯儼k=n(n+1)/2丂傛傝
楢懕曗惓
弴埵偼弴彉広搙偱棧嶶検乮僷儔儊僩儕僢僋偺婃嫮惈偑偙偙偱傕搊応乯
偙偺傑傑埖偆偲惓婯暘晍偲崌傢側偄偺偱偦傟偧傟0懁偵岦偐偭偰0.5偩偗僔僼僩
嬤帡幃偱n亝25偺晹暘傪寁嶼偟傑偟偨
P72(椺戣10)
t専掕傕峴偆偲丒丒丒
乮弴埵傪尒偰偄傞丒丒丒奜傟抣偺掱搙偼塭嬁偟側偄乯
Mann-Whitney専掕
擇昗杮偵側傞偲傗傗偙偟偔側傞偺偼僷儔儊僩儕僢僋専掕偲摨偠P99嶲徠
専掕摑寁検
懠孮偐傜尒偨帺孮偺屄乆偺弴埵亅侾偺憤榓傪媮傔偰専掕摑寁検偲偟偰偄傞
侾丗偁傞孮乮A乯偺抣偦傟偧傟偑傕偆堦曽偺孮乮B乯偵擖偭偨偲偟偨偲偒偵乮A偺乯偦偺抣傛傝傕乮B偺孮偺側偐偱乯抣偑戝偒偄屄悢傪僇僂儞僩偡傞丅乮A孮偺乯慡偰偵偮偄偰峴偄榓傪偲傞
俀丗A偲B傪擖傟懼偊偰侾丗偲摨條偺寁嶼傪偡傞偐丄岞幃偱B孮偺榓傪媮傔彫偝偄曽傪専掕摑寁検U偲偡傞
摓払搙妋擣
侾乯旐尡幰侾俀柤偺塣摦慜屻偺寣拞儂儖儌儞A偺應掕傪偟偨丅塣摦偵傛傝A抣偼曄摦偟偨偲尵偭偰傛偄偐僷儔儊僩儕僢僋丄媦傃僲儞僷儔儊僩儕僢僋専掕傪偣傛
| ID | 塣摦慜 | 塣摦屻 |
|---|---|---|
| 1 | 121 | 140 |
| 2 | 100 | 142 |
| 3 | 173 | 174 |
| 4 | 143 | 137 |
| 5 | 134 | 160 |
| 6 | 125 | 151 |
| 7 | 158 | 190 |
| 8 | 156 | 149 |
| 9 | 176 | 210 |
| 10 | 165 | 162 |
| 11 | 140 | 180 |
| 12 | 167 | 200 |
栤戣
丂
曗懌
|
嫵壢彂奩摉儁乕僕 戞0復乮P5-6乯 戞2復乮P46乯 戞4復乮P56-62乯 戞5復乮P78-87乯 戞10復乮P195-199乯 徯夘偟偨榖側偳 儅儞儌僌儔僼傿乕偺擕偑傫敾暿崲擄椺揱偊偢乧帺帯懱偺7妱乮撉攧怴暦乯 http://www.yomiuri.co.jp/national/20160611-OYT1T50095.html http://girlschannel.net/topics/785359/ 乽偁傞乿偲敾抐弌棃側偗傟偽乽側偄乿丒丒丒僌儗乕僝乕儞偼乽側偄乿徯夘偟偨僯儏乕僗偺榖 乽側偄乿偲敾抐弌棃側偗傟偽乽偁傞乿丒丒丒僌儗乕僝乕儞偼乽偁傞乿壖愢専掕偺榑朄 |
戞11夞丂寁悢抣僨乕僞偺専掕
摓払栚昗侾侾亅侾擇崁暘晍偲惓婯暘晍偺娭學傪愢柧偱偒傞
侾侾亅俀僇僀擇忔暘晍偲惓婯暘晍偺娭學傪愢柧偱偒傞
寁検抣偲寁悢抣
寁検抣丒丒丒検傪應掕寁悢抣丒丒丒昿搙傪應掕
昿搙傪昿搙偱妱偭偨傕偺偼寁悢抣乮妱崌亖斾棪乯
懪棪乮昿搙棪偱偼柍偄偗偳乯
検揑曄検偼昿搙偺應掕傕弌棃傞
擇崁暘晍
昗杮偺戝偒偝=n帠徾偺婲偙傞妋棪=p
r=np=n夞帋峴傪孞傝曉偟偨偲偒偵帠徾偺婲偙傞夞悢乮婜懸搙悢乯
擇崁暘晍仺np偑俆傛傝傕戝偒偄乮n偑廫暘偵戝偒偄応崌丂嫵壢彂偱偼np亞10 and n(1-p)亞10乯惓婯暘晍偵嬤帡
冊俀忔暘晍
嫵壢彂P128-129冊俀忔暘晍丒丒丒曣暘嶶傪悇掕偱偒傞妋棪暘晍
帺桼搙偲偲傕偵暘嶶傕憹壛偡傞
惓婯暘晍偐傜忋懁妋棪傪寁嶼
僶儔僣僉偺榖側偺偱壓懁偺妋棪偼僶儔偮偒偡偓偰偄側偄妋棪
丂仺丂惓婯暘晍偺椉懁2.5%偼僇僀擇忔偱忋懁偵廤栺偝傟傞
冊俀忔専掕
弌尰搙悢Oi偲婜懸搙悢Ei偺僘儗傪専掕婜懸搙悢偼梌偊傜傟偨忣曬偐傜悇應偟偨棟榑揑偵媮傔偨搙悢
揔崌搙偼懳徾偑偁傞忦審壓偵偍偄偰憐掕偝傟傞斾棪乮堦條丂係丗俁丗俀丗侾丂偲偐乯偵婎偯偒悇應
撈棫惈偼偦傟偧傟偺梫場傪梡偄偰悇應
婜懸搙悢偑掅偄応崌丄偦偺傑傑巊偊側偄偑丄寁嶼偼妝
Fisher偺捈愙妋棪朄偼偄偮偱傕巊偊傞偑寁嶼戝曄
乮僐儞僺儏乕僞傪巊偊傞帪戙乯
屘偵嫵壢彂偱偼俀亊俀昞埲奜弌偰偙側偄乮峫偊曽偼堦弿乯
傛偔偁傞丠娫堘偊
搙悢側偺偵斾棪乮侾侽侽亾乯偵捈偟偰偐傜専掕偲偐
亙妋擣亜
嫵壢彂P135偺寁悢抣傪10攞偡傞偲
| 栻嵻孮 | 婾栻孮 | ||
|---|---|---|---|
| 亄 | 俋侽 | 俁侽 | 侾俀侽 |
| 亅 | 俀侾侽 | 俀俈侽 | 係俉侽 |
| 俁侽侽 | 俁侽侽 |
摓払搙妋擣
侾乯僀僠儘乕慖庤偺懪棪傪.350偲偡傞偲偒丄係懪悢僲乕僸僢僩偵側偭偰偟傑偆妋棪偼偳偺掱搙偐媮傔傛俀乯偁傞徢忬偵懳偟偰栻暔椕朄傪峴偭偨応崌侾擭埲撪偵侾俆亾偺恖偑嵞敪偡傞丅怴栻傪奐敪偟帋尡揑偵俀侽侽椺偺姵幰偵搳梌偟偨偲偙傠丄嵞敪椺偑俀侽椺偁偭偨丅怴栻偵岠壥偑偁傞偐専掕偣傛
俁乯埲壓偺帯椕朄偲惗懚巰朣悢偺娭學偐傜帯椕朄偵傛傝揮婣偑堎側傞偐専掕偣傛
| 帯椕朄A | 帯椕朄B | ||
|---|---|---|---|
| 惗懚 | 俁侽 | 俀俆 | 俆俆 |
| 巰朣 | 俀侽 | 俁俆 | 俆俆 |
| 俆侽 | 俇侽 |
曗懌
|
嫵壢彂奩摉儁乕僕 戞7復乮P114-140乯 徯夘偟偨榖側偳 恖岥僺儔儈僢僪偺榖丅偪側傒偵擔杮偺応崌暩屵偺塭嬁偱恖岥偑棊偪崬傫偱偄傞擭乮侾俋俇俇乯偑偁傝傑偡丅 変偑崙偺恖岥僺儔儈僢僪亅擔杮偺摑寁2016乮憤柋徣摑寁嬊乯傛傝 http://www.stat.go.jp/data/nihon/g160402.htm
抋惗擔偺榖傕偟傑偟偨偑丄夁嫀偵挷傋偰偄偨曽偑偍傜傟傑偟偨丅4寧2擔懡偄偱偡偹
m3偱乽乽掅妛擭僋儔僀僔僗乿丄6妱嫮偑幚姶仧Vol.1 乿偲偄偆婰帠偑弌偰偄偨偲偄偆榖傪偟傑偟偨丅 偦偺拞偱徯夘偝傟偰偄傞傾儞働乕僩挷嵏偺寢壥偑岞昞偝傟偰偄傞偺偱儕儞僋挘偭偰偍偒傑偡丅 堛妛惗偺妛椡偵娭偡傞傾儞働乕僩挷嵏寢壥曬崘彂乮暯惉28擭1寧乯慡崙堛妛晹挿昦堾挿夛媍 https://www.ajmc.jp/download/gakuryoku-27.pdf Fisher偺捈愙妋棪寁嶼朄偼柺搢偔偝偄偲偄偆榖偱擺傔傑偟偨偑丄嫵壢彂P137乣傪嶲峫偵幚嵺偵暅廗偱寁嶼傪偟偰傒偰偔偩偝偄丅 |
戞12夞丂撈棫懡孮娫偺斾妑
摓払栚昗侾俀亅侾F暘晍偲僇僀擇忔暘晍偺娭學傪愢柧偱偒傞
侾俀亅俀暘嶶暘愅偲懡廳専掕偺堘偄傪愢柧偱偒傞
F暘晍
僇僀擇忔暘晍偲摨偠偔暘嶶偵娭偡傞妋棪暘晍偦傟偧傟偺孮偺僇僀擇忔抣偺斾亖暘嶶偺斾丒丒丒俥抣乮俥偼僼傿僢僔儍乕偺俥乯
F暘晍偲t暘晍偺娭學
t^2(兯)=F(1,兯)
F暘晍偲僇僀擇忔暘晍偺娭學
冊^2(兯)=兯亊F乮兯,亣乯
F専掕偺榖
摍暘嶶惈偺専掕丒丒丒暘嶶斾傪媮傔偰F抣傛傝敾掕乽2孮偺暘嶶偼堎側傞偲偼尵偊側偄乿丒丒丒婣柍壖愢傪婞媝偱偒側偄乮曐棷乯
丂 乽2孮偺暘嶶偵嵎偑柍偄偲偼尵偊側偄偲偼尵偊側偄乿偲偄偆擔杮岅偵側傞
懡孮娫偺斾妑
嫵壢彂P142孮暘偗丒丒丒弴彉広搙埲忋偱偦偺娭楢傪傒偨偄仺摨帪斾妑
孮暘偗丒丒丒柤媊広搙or娭楢傪尒傞傢偗偱偼側偄仺懡廳斾妑
摨帪斾妑偟偰嵎偑偁偭偨偐傜懡廳斾妑偡傞偲偄偆偺偼丄壗傪弎傋偨偄偐偵傛傞偑丒丒丒
P154嶲徠
摨帪斾妑
偙傟傑偱偲摨偠傛偆偵惓婯暘晍偵廬偆偐斲偐偺榖偵側傞仺P159乮P99偲懳斾偝偣側偑傜乯堦尦攝抲暘嶶暘愅
孮娫暘嶶偲孮撪暘嶶偺斾傪偲傞Kruskal-Wallis専掕
嫵壢彂P152P154椺戣32偺僨乕僞偱奜傟抣偺榖傕
懡廳専掕
嫵壢彂P207偦傟偧傟偺専掕偑撈棫偟偨壖愢偵傕偲偯偄偨傕偺偲峫偊偰椙偄偐丠
堦楢偺傕偺偱偁傟偽懳棫壖愢傪峫偊偨偲偒偵桳堄悈弨偑俆亾偲尵偄側偑傜俆亾偵側偭偰偄側偄偺偱偼丠
懡廳偵専掕偡傞偙偲偱偳傟偐偁偨傟偽婣柍壖愢偼婞媝偱偒傞偺偱椺偊偽3孮憤摉偨傝偩偲桳堄悈弨0.05偱懡廳専掕乮6捠傝乯偡傞偲0.265偵側偭偰偟傑偆丅
埲壓偼P146椺戣32偱夝愢
桳堄妋棪曗惓朄
Bonferrini偺応崌偼6捠傝専掕偡傞偺偱偁傟偽丄堦専掕偁偨傝偺桳堄悈弨偩偲0.05/6=0.0083偲側傞丅慡懱偱偼1-(1-0.00833)^6=1-0.95103=0.0490Sidak曗惓偺応崌偼摨條偵1-(1-0.05)^(1/6)=0.008512丂1-(1-0.008512)^6=1-0.95=0.0500
懡孮偵側傞傎偳専掕偁偨傝偺桳堄悈弨偑壓偑傞仺嵎偑弌偵偔偄
懡廳斾妑朄
僷儔儊僩儕僢僋朄Tukey朄丒丒丒奺儁傾偵懳偡傞暯嬒抣偺嵎偺専掕
Dunnett専掕丒丒丒堦偮偺懳徾孮偲偺懳斾
僲儞僷儔儊僩儕僢僋朄
Dunn朄
摓払搙妋擣
侾乯P151墘廗14偱70dB乣90dB偺僨乕僞傪堦尦攝抲暘嶶暘愅傪偟偨応崌偳偺傛偆側寢壥偵側傞偐媮傔傛俀乯P148椺戣30傛傝懡廳専掕偺寁嶼寢壥傪乮夋柺忋偵乯帵偡丅Bonferroni曗惓傪偟偨偆偊偱専掕寢壥傪帵偣
曗懌
|
寢嬊摨帪斾妑偼僇僀擇忔専掕偺帪偲摨條偵堘偆偙偲偑暘偐偭偰傕偳偺娭學偑堘偆偐傑偱偼傢偐傜側偄 嫵壢彂奩摉儁乕僕 戞8復乮P141-159乯 戞9復乮P207-209乯 嶲峫帒椏 暘愅朄偺懨摉惈妋擣偵娭偡傞僈僀僟儞僗乮擾尋婡峔乯傛傝 http://www.naro.affrc.go.jp/org/nfri/yakudachi/datosei/pdf/F_and_Chisquare.pdf F暘晍偲偼壗偐丠乮傛偆偙偦丄壔妛昗弨暔幙偺晄妋偐偝傊偺偄偞側偄 乮嶻嬈媄弍憤崌尋媶強乯乯 https://staff.aist.go.jp/t.ihara/f.html 嶨択宯 僯儞僯僋椏棟偺審偼丄嬥梛擔偵徚旓検偑懡偔偰擔梛擔偼彮側偄偺偱偼側偄偐偲偄偆壖愢乮梛擔偵傛傝堘偄偑偁傞乯 偪側傒偵椏棟偼偙傟丅旤枴偟偐偭偨偱偡
懡廳専掕偺偔偩傝偼丄儌儎儌儎偟偰偄傞曽偑傑偩偍傜傟傞偙偲偱偟傚偆丅巹偵幙栤偵偒偨妛惗偼堄枴傪棟夝偟偰擺摼偺條巕丅梫偼懳棫壖愢偼壗丠偲峫偊傟偽丄銬偵棊偪傞傛偆偵巚偄傑偡丅 |
戞13夞丂懡曄検夝愅
摓払栚昗侾俁亅侾憡娭學悢偲曃憡娭學悢偺堘偄傪棟夝偡傞
侾俁亅俀廳夞婣暘愅偵偍偄偰偳偺傛偆偵曄悢偑慖偽傟偰偄傞偐愢柧偱偒傞
懡曄検夝愅偵偮偄偰
嫵壢彂P5懡偔偺曄検傪梡偄偰扵嶕揑偵 暘椶丒梊應丒丒丒乮廳夞婣暘愅乯
梫栺丒丒丒奜揑婎弨偑側偄乮庡惉暘暘愅乯
乽娭學偁傝偦偆側僨乕僞傪廤傔偨偗偳偳偆偟偨傜傑偲傑傞偺傗傜乿偲偄偆擸傒傪夝寛偟偰偔傟傞柌傪尒傗偡偄
廳夞婣暘愅
嫵壢彂P193乮夞婣捈慄偺榖傪巚偄弌偡仺扨夞婣暘愅乯
夞婣丒丒丒尦偵栠傞丒丒丒壗傜偐乮掕棟傗娭學乯偵婎偯偒栠偭偰偄偔
扨夞婣暘愅
嫵壢彂P181夞婣學悢丒丒丒Y=a+bX偺b
亙暅廗亜r偼嫟暘嶶
扨憡娭學悢偺専掕丒丒丒乮桳堄偵憡娭偑偁傞偐斲偐乯嫵壢彂P168椺戣33
摨條偵 夞婣學悢偺専掕
Ti=^Bi乛SE
帺桼搙=n-2偺t暘晍
摨條偵専掕
憡娭學悢偲夞婣學悢
夞婣捈慄偺応崌偼廬懏曄悢偲撈棫曄悢偺娭學傪a崁偲b崁乮夞婣學悢乯偵暘棧偝偣偰峫偊傞憡娭學悢偼暘棧偝偣偢偵偦傟偧傟偺僶儔僣僉傪婎偵媮傔偰偄傞
X偲Y傪擖傟懼偊傞偲夞婣學悢偼曄傢傞丅憡娭學悢偼曄傢傜側偄
曃憡娭學悢偲曃夞婣學悢
憡娭峴楍丂扨憡娭偲曃憡娭
幚懺偲偟偰偼憡娭娭學偱峔傢側偄偑丄偦傟偧傟偺曄検偺娭學惈傪柧傜偐偵偡傞偵偼曃憡娭懡偔偺曄検偵懳偡傞憡娭仺憡娭峴楍
P172墘廗17偵乮崑夣偵乯擭楊傪擖傟偰暘愅偡傞偲丒丒丒乮ID1乣5傪9嵨丂6乣10傪10嵨丂11乣15傪11嵨乯
攛妶検偺榖側偺偵丒丒丒
5.2丂曃憡娭偲偼乮傾僀僗僋儕乕儉壆偝傫偱妛傇妝偟偄摑寁妛劅劅憡娭偐傜場巕暘愅傑偱劅劅乯
http://kogolab.chillout.jp/elearn/icecream/chap5/sec2.html
廳夞婣暘愅偺奣梫
Y=b0+b1x1+b2x2+(拞棯)+bnxn
曗惓 R2丒丒丒帺桼搙廋惓嵪傒寛掕學悢丒丒丒侾偵嬤偄傎偳椙岲側儌僨儖丅
t抣丒丒丒學悢偑0偐斲偐偺専掕
懡廳嫟慄惈
捠徧丗儅儖僠僐愢柧曄悢偺娫偵憡娭偑偁傞偲偍偐偟偔側傞乮忋偺榖傕偦傟乯
憡娭偺偁傞曄悢傪堦偮偵傑偲傔傞側偳丒丒丒
摓払搙妋擣
侾乯P162偺憡娭椺A乣C偵偮偄偰柍憡娭偺専掕傪峴偊俀乯崱傑偱偺摓払搙妋擣偱摿偵夝愢傪媮傔偨偄栤戣傪婰偟偰偔偩偝偄乮扐偟3栤埲撪乯
曗懌
|
扵嶕揑側榖側偺偱専掕寢壥偼丄乽傕偟傕壖愢偑偁傞側傜偽乿揑偵峫偊側偄偲偄偗側偄丅 偦偺曄検偺堄枴崌偄偼暘愅壆偼尷奅偑偁傝懳榖偺拞偱攃埇偟偰偄偒傑偡丅屘偵幚嵺偺尋媶偱偼尋媶幰偲僨傿僗僇僢僔儑儞偟側偑傜偺擔乆偱偡丅 嫵壢彂奩摉儁乕僕 戞0復乮P5乯 戞9復乮P168-172,P181-188乯 戞10復乮P193-194乯 嶲峫帒椏 嶨択宯 |
戞14夞丂惗懚帪娫暘愅
摓払栚昗侾係亅侾僇僾儔儞儅僀儎乕朄偵傛傞惗懚棪傪寁嶼偡傞偙偲偑弌棃傞
侾係亅俀儘僌儔儞僋専掕偵傛傞惗懚棪偺嵎偺専掕傪峴偆偙偲偑弌棃傞
惗懚帪娫暘愅偼帯椕朄摍偺昡壙偵帪娫幉傪娷傔偨傕偺
僀儀儞僩敪惗傑偱偺帪娫偵傛傞暘愅
惗懚棪
惗懚棪偵偼寁嶼曽幃偑暋悢揹嶼婡偺晛媦偵傛傝Kaplan-Meier朄偱傕梕堈偵寁嶼弌棃傞帪戙
偦傕偦傕棪偼斾偺摿庩側宍懺偱扨埵帪娫偁偨傝偺僀儀儞僩悢傪昞傢偡
恖擭朄乮嶲峫乯戝嶃曐寬堛椕戝妛堛椕忣曬妛2015偺奩摉儁乕僕乯
http://www.medbb.net/education/ohsumedinfo2015/index.html#13
Kaplan-Meier偱媮傔傞旕僀儀儞僩敪惗乮惗懚乯棪亖1-僀儀儞僩敪惗乮巰朣乯棪偼丄棪偱偼柍偔帪揰僀儀儞僩乮巰朣乯妱崌側偺偱拲堄
亙嶲峫亜
姵幰偺惗懚棪乮抧堟偑傫搊榐慡崙嫤媍夛乯
http://www.jacr.info/about/survival.html
捈愙朄偼妱崌丅拞搑懪偪愗傝偑偁傞偲崲傞
惗柦曐尟悢棟朄傕妱崌丅拞搑懪偪愗傝偵偮偄偰偼侾乛俀傪娤嶡婜娫偵娷傔偰偄傞偑僀儀儞僩敪惗乮巰朣乯幰偺娤嶡婜娫傪峫椂偟偰偄側偄偺偱棪偱偼柍偄乮峫椂偟偰偄偨傜恖擭偁偨傝乮棪乯偵側傞乯
僇僾儔儞儅僀儎乕朄偵傛傞僀儀儞僩敪惗棪偺寁嶼
屄昜僨乕僞| 姵幰ID | 恌抐柤 | 嵞敪帪婜 | 姵幰ID | 恌抐柤 | 嵞敪帪婜 | 姵幰ID | 恌抐柤 | 嵞敪帪婜 | 姵幰ID | 恌抐柤 | 嵞敪帪婜 | 姵幰ID | 恌抐柤 | 嵞敪帪婜 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | b | 3 | 11 | a | 8 | 21 | b | 9 | 31 | b | 24+ | 41 | a | 3+ |
| 2 | b | 5 | 12 | b | 14 | 22 | b | 18 | 32 | a | 12 | 42 | b | 8 |
| 3 | b | 6 | 13 | b | 9 | 23 | a | 12+ | 33 | a | 3+ | 43 | b | 24+ |
| 4 | b | 14 | 14 | a | 1 | 24 | a | 3 | 34 | b | 13 | 44 | a | 5+ |
| 5 | a | 7+ | 15 | a | 2 | 25 | b | 17+ | 35 | b | 17 | 45 | b | 14 |
| 6 | a | 14 | 16 | a | 3 | 26 | a | 7 | 36 | a | 3 | |||
| 7 | a | 17 | 17 | a | 13 | 27 | a | 8 | 37 | b | 15 | |||
| 8 | b | 21 | 18 | b | 21 | 28 | a | 12 | 38 | b | 13 | |||
| 9 | b | 21 | 19 | b | 16 | 29 | b | 12+ | 39 | a | 21 | |||
| 10 | b | 16 | 20 | b | 24+ | 30 | a | 1 | 40 | b | 18 |
幚應惓忢棪偺寁嶼
幘姵a| 恌抐偐傜偺寧悢 | 寧奐巒帪偺惓忢悢 | 敪徢悢 | 拞搑懪偪愗傝悢 | 敪徢妱崌 | 惓忢妱崌 | 椵愊惓忢棪 |
|---|---|---|---|---|---|---|
| 1 | 20 | 2 | 0 | 0.100 | 0.900 | 0.900 |
| 2 | 18 | 1 | 0 | 0.056 | 0.944 | 0.850 |
| 3 | 17 | 3 | 2 | 0.176 | 0.824 | 0.700 |
| 5 | 12 | 0 | 1 | 0.700 | ||
| 7 | 11 | 1 | 1 | 0.091 | 0.909 | 0.636 |
| 8 | 9 | 2 | 0 | 0.222 | 0.778 | 0.495 |
| 12 | 7 | 2 | 1 | 0.286 | 0.714 | 0.354 |
| 13 | 4 | 1 | 0 | 0.250 | 0.750 | 0.265 |
| 14 | 3 | 1 | 0 | 0.333 | 0.667 | 0.177 |
| 17 | 2 | 1 | 0 | 0.500 | 0.500 | 0.088 |
| 21 | 1 | 1 | 0 | 1.000 | 0.000 | 0.000 |
| 恌抐偐傜偺寧悢 | 寧奐巒帪偺惓忢悢 | 敪徢悢 | 拞搑懪偪愗傝悢 | 敪徢妱崌 | 惓忢妱崌 | 椵愊惓忢棪 |
|---|---|---|---|---|---|---|
| 3 | 25 | 1 | 0 | 0.040 | 0.960 | 0.960 |
| 5 | 24 | 1 | 0 | 0.042 | 0.958 | 0.920 |
| 6 | 23 | 1 | 0 | 0.043 | 0.957 | 0.880 |
| 8 | 22 | 1 | 0 | 0.045 | 0.955 | 0.840 |
| 9 | 21 | 2 | 0 | 0.095 | 0.905 | 0.760 |
| 12 | 19 | 0 | 1 | 0.760 | ||
| 13 | 18 | 2 | 0 | 0.111 | 0.889 | 0.676 |
| 14 | 16 | 3 | 0 | 0.188 | 0.813 | 0.549 |
| 15 | 13 | 1 | 0 | 0.077 | 0.923 | 0.507 |
| 16 | 12 | 2 | 0 | 0.167 | 0.833 | 0.422 |
| 17 | 10 | 1 | 1 | 0.100 | 0.900 | 0.380 |
| 18 | 8 | 2 | 0 | 0.250 | 0.750 | 0.285 |
| 21 | 6 | 3 | 0 | 0.500 | 0.500 | 0.143 |
| 24 | 3 | 0 | 3 | 0.143 |
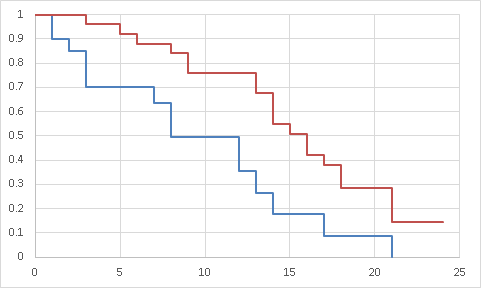
幘姵a丗惵慄
幘姵b丗愒慄
儘僌儔儞僋専掕
僇僀擇忔暘晍偵傛傞専掕傪峴偆乮婜懸搙悢偲斾妑偟偰僶儔僣僉偑偁傞偐斲偐乯
僀儀儞僩敪惗枅偺僋儘僗昞乮僇僢僐撪偼婜懸搙悢乯
侾儢寧| 敪徢悢 | 寬忢悢 | 崌寁 | |
| 徢椺a | 2(0.889) | 18(19.111) | 20 |
| 徢椺b | 0(1.111) | 25(24.889) | 25 |
| 崌寁 | 2 | 43 | 45 |
| 敪徢悢 | 寬忢悢 | 崌寁 | |
| 徢椺a | 1(0.419) | 17(16.581) | 18 |
| 徢椺b | 0(0.581) | 25(24.419) | 25 |
| 崌寁 | 1 | 42 | 43 |
幚應滊姵棪媦傃婜懸搙悢
| 恌抐偐傜偺寧悢 | a娤嶡搙悢 | a懪偪愗傝悢 | a憤恖悢 | a婜懸搙悢 | b娤嶡搙悢 | b懪偪愗傝悢 | b憤恖悢 | b婜懸搙悢 |
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 0 | 20 | 0.889 | 0 | 0 | 25 | 1.111 |
| 2 | 1 | 0 | 18 | 0.419 | 0 | 0 | 25 | 0.581 |
| 3 | 3 | 2 | 17 | 1.619 | 1 | 0 | 25 | 2.381 |
| 5 | 0 | 1 | 12 | 0.333 | 1 | 0 | 24 | 0.667 |
| 6 | 0 | 0 | 11 | 0.324 | 1 | 0 | 23 | 0.676 |
| 7 | 1 | 1 | 11 | 0.333 | 0 | 0 | 22 | 0.667 |
| 8 | 2 | 0 | 9 | 0.871 | 1 | 0 | 22 | 2.129 |
| 9 | 0 | 0 | 7 | 0.500 | 2 | 0 | 21 | 1.500 |
| 12 | 2 | 1 | 7 | 0.538 | 0 | 1 | 19 | 1.462 |
| 13 | 1 | 0 | 4 | 0.545 | 2 | 0 | 18 | 2.455 |
| 14 | 1 | 0 | 3 | 0.632 | 3 | 0 | 16 | 3.368 |
| 15 | 0 | 0 | 2 | 0.133 | 1 | 0 | 13 | 0.867 |
| 16 | 0 | 0 | 2 | 0.286 | 2 | 0 | 12 | 1.714 |
| 17 | 1 | 0 | 2 | 0.333 | 1 | 1 | 10 | 1.667 |
| 18 | 0 | 0 | 1 | 0.222 | 2 | 0 | 8 | 1.778 |
| 21 | 1 | 0 | 1 | 0.571 | 3 | 0 | 6 | 3.429 |
崱夞偼擇偮偺孮偺斾妑丒丒丒帺桼搙k亖n-1=1
俷1亖a娤嶡搙悢偺憤榓=15
俤1亖a婜懸搙悢偺憤榓=8.549
俷2亖b娤嶡搙悢偺憤榓=20
俤2亖b婜懸搙悢偺憤榓=26.451
専掕摑寁検冊^2亖6.441
冊^2乮1,0.95乯=3.8415
屘偵婣柍壖愢傪婞媝偟懳棫壖愢傪嵦戰偡傞乮a,b偺嵞敪棪偵嵎偑偁傞乯
曗懌
|
摓払搙妋擣摿偵夝愢傪媮傔偨偄栤戣傾儞働乕僩寢壥 傾儞働乕僩乮13夞庼嬈摓払搙妋擣乯 夞廂悢丂丂丂侾侽侽審 桳岠夞摎悢丂丂俇侾審 侾埵丂俀俉丂戞7夞丂憡懳婋尟搙 丂侾乯儕僗僋斾乮僐儂乕僩乯乮100/2000乯乛乮50/2000乯亖2.0丂僆僢僘斾乮徢椺懳徠乯乮50/30乯乛乮50/70乯亖2.33丂俀乯憡懳婋尟偺崁嶲徠丂俁乯僨乕僞偐傜偦傟偧傟偺孮偺儕僗僋傪悇掕偱偒側偄偐傜丂係乯棯 俀埵丂俀俆丂戞8夞丂専掕偺尨棟 丂侾乯冃亖3cm偺帪 16恖丒丒倸亖(137-40)乛乮3乛併16乯亖-4 丂 P=P(|z|亞4)亙P(|Z|亞2.58)=0.01 丂 埲壓棯 丂俀乯棯 俁埵丂侾俈丂戞4夞丂暯嬒抣偺悇掕 丂奩摉庼嬈曗懌嶲徠 係埵丂侾俇丂戞9夞丂僷儔儊僩儕僢僋専掕 丂侾乯P59椺戣8嶲徠 丂俀乯P80椺戣12嶲徠 嫵壢彂奩摉儁乕僕 嶲峫帒椏 嶨択宯 |
戞15夞丂傑偲傔
摓払栚昗侾俆亅侾偙傟傑偱偺庼嬈偱棟夝偟偰偄側偐偭偨晹暘傪棟夝偡傞
戞13夞栚傾儞働乕僩婰弎晹暘偵懳偡傞夞摎
3栤偺傒偲尵傢偢慡晹夝愢偟偰梸偟偄
庼嬈偺撪梕偵増偭偰偄傞偺偱暅廗偡傞偲婎杮夝偗傑偡丅偦偺忋偱暘偐傜側偄晹暘傪嫵偊偰偄偨偩偗傞偲僺儞億僀儞僩傾僪僶僀僗偱棟夝偵摫偗傑偡奺専掕偺巊偄暘偗傪嫵偊偰梸偟偄
乮僇僀擇忔専掕偑偳偙偱惗偒偰偔傞偺偐傢偐傜側偄偱偡乯偲傝偁偊偢嫵壢彂P4乣P7傪撉傫偱棊偪拝偄偰偔偩偝偄
丂
偦傕偦傕t専掕偭偰壗
t暘晍偦偺傕偺偼戞4夞偺乽曣昗弨曃嵎偑枹抦偺応崌偺嬫娫悇掕乿偺偲偙傠傪撉傫偱傒偰偔偩偝偄丅壗屘晄曃暘嶶偱偼n-1偱妱傞偺偐
戞3夞摓払搙妋擣栤戣係乯曣暘嶶冃^2=侾乛俶儼乮倃i-兪)^2
昗杮暘嶶倱^2亖侾乛n儼乮倶j-倶bar)^2
乮倶j-倶bar亖(倶j-兪)-(倶bar-兪)傪戙擖乯
昗杮暘嶶倱^2亖侾乛n儼((乮倃j-兪)^2-2(倶j-兪)(倶bar-兪)+(倶bar-兪)^2)
丂丂丂丂丂丂亖侾乛n儼乮倃j-兪)^2-2(倶bar-兪)侾乛n儼(倶j-兪)+(倶bar-兪)^2
丂丂丂丂丂丂亖侾乛n儼乮倃j-兪)^2-(倶bar-兪)^2丂丒丒丒丂侾幃
曣暯嬒兪傪巊偊側偄偨傔昗杮暘嶶偼(倶bar-兪)^2亖岆嵎暘嶶乮昗弨岆嵎偺擇忔乯暘偩偗彫偝偔側傞
(倶bar-兪)^2亖侾乛n(侾乛n儼乮倃j-兪乯^2乯
侾幃偵戙擖
昗杮暘嶶倱^2亖侾乛n儼乮倃j-兪)^2亅侾乛n(侾乛n儼乮倃j-兪乯^2乯
丂丂丂丂丂丂亖乮侾亅侾乛値乯侾乛n儼乮倃j-兪)^2
曣暯嬒傪梡偄偨暘嶶侾乛n儼乮倃j-兪)^2丒丒丒晄曃暘嶶
亪晄曃暘嶶亖n/(n-1)倱^2=n/(n-1)丒侾乛n儼乮倶j-倶bar)^2
丂丂丂丂丂亖1/(n-1)儼(倶j-倶bar)^2
丂偲偄偆偙偲偱丄昗杮偺暘嶶傪媮傔傞応崌偼捠忢偺暘嶶偺傛偆偵n偱妱傞偺偱偼側偔乮n-1乯偱妱偭偰曣暘嶶傪悇掕偟傑偡乮晄曃暘嶶乯