大阪保健医療大学 医療情報学2015
(保健医療学部リハビリテーション学科 作業療法学専攻)
シラバス
シラバスでは筆記試験100%ですが、筆記試験において失点の部分が生じた場合「到達度確認」の実施状況などを加味し補填した上で評価することとします。
本講義の医療統計と統計学の関連について
大阪保健医療大学では医療情報学の他に、統計学を受講できます。医療情報学では統計および医療統計の基礎的な部分の理解を目的とします。
統計学では実際にPCを用いて有意差検定が出来るように、データ入手から分析まで行うことで必要な能力を身につけていくことを目的としています
課題(任意)提出について
講義支援システム(ムードル Moodle)から提出してくださいhttps://moodle.ohsu.ac.jp/login/index.php
ワード・エクセルで提出のこと
ファイル名は「[学籍番号][氏名]医療情報学課題[X]」 [X]は授業回数に適宜置換
本文最初に課題名・氏名・課題名等を記すこと
授業内容に関する質問について
次回の授業の冒頭に説明ただし説明しない場合あり(授業範囲を超える場合)・・・その旨言います
講義支援システム(ムードル Moodle)から提出してください
https://moodle.ohsu.ac.jp/login/index.php
ワード・エクセルで提出のこと
ファイル名は「[学籍番号][氏名]医療情報学質問[X]」 [X]は授業回数に適宜置換
本文最初に課題名・氏名を記すこと
課題(任意)提出および質問受付は15回目の授業開始前まで(最終回以降説明・コメントの紹介できないため))
自己紹介
http://researchmap.jp/medbb/医療情報の世界 医療情報技師の役割について
http://www.medbb.net/education/joho20150613/index.html
授業メニュー
第1回 情報学(Ⅰ)-情報とは
第2回 情報学(Ⅱ)-情報量の計算について
第3回 情報学(Ⅲ)-ネットワーク技術について
第4回 情報学(Ⅳ)-情報セキュリティ
第5回 保健医療情報システム(Ⅰ)-医用画像について
第6回 保健医療情報システム(Ⅱ)-電子カルテについて
第7回 保健医療情報システム(Ⅲ)-施設内の情報システムについて
第8回 保健医療情報システム(Ⅳ)-施設間の情報システムについて
第9回 統計基礎(Ⅰ)-尺度・度数分布について
第10回 統計基礎(Ⅱ)-代表値について
第11回 統計基礎(Ⅲ)-散布度について
第12回 医療統計(Ⅰ)-病院の統計資料
第13回 医療統計(Ⅱ)-比と率と割合
第14回 医療統計(Ⅲ)-相対危険度
第1回 情報学(Ⅰ)-情報とは
到達目標1-1データ 情報 知識の違いを説明することが出来る
1-2情報量bitと確率の関係について説明することが出来る
データと情報と知識の関係
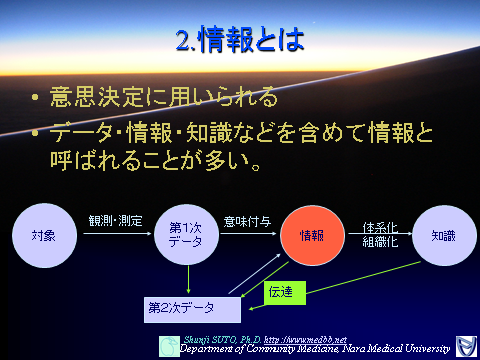
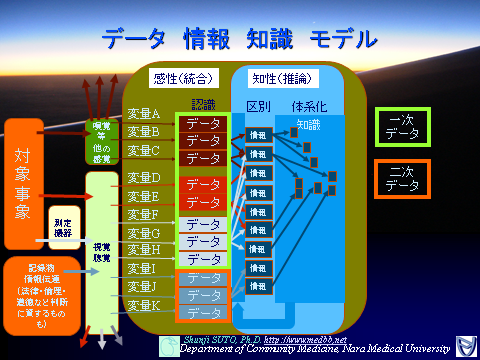 データ:
データ:一次データと二次データの違い。
一次・・・ライブ。対象からダイレクト
二次・・・既に記録されたもの。まとめられたもの
情報:
データに意味を付与したもの
ただし受信者の特性に依存
知識:
情報を体系化したもの。
受信者の知性は当然だが、提供されているデータや情報としての理解の度合いや誤解によって知識構造体に違いが出てくる。
情報の量
bit:シャノンの情報理論AなのかAじゃないのか?明確に指定できる情報・・・1bit
事象の起こる確率によって決まる。確率の低い事象を確定する情報ほど大きくなる
事象の起こる確率(均等ならば選択肢の数)によって情報の量が決まる
→ 選択肢を用意しないと情報は取り扱えない
デジタルの世界では1と0の情報の組み合わせであらゆるデータを取り扱っている
様々なエラー
情報を送っても受信者はそれを情報として認識しない
情報を送っても受信者はそれを曲解して違う情報として受けとる
情報を送っていないのに受信者は勝手に情報として受け取る
第2回 情報学(Ⅱ)-情報量の計算について
到達目標2-1情報量の計算が出来る
2-2補助単位について説明できる
2-2画像や音や文字などどのようにして情報化(デジタル情報化)されているか説明することが出来る
情報量の定義
yes/Noを区別(選択肢2つから1に)させる情報・・・1bit選択肢4つから1にさせる情報・・・2bit
選択肢8つから1にさせる情報・・・3bit
選択肢は2のるい乗(べき乗)になる。
対数(log)・・・るい乗(べき乗)を求めることが出来る→選択肢から情報量を求められる
文字の情報量
英数字・・・7bit+カナ・・・8bit=(1byte)半角文字
漢字は倍の2yte(全角文字)
情報量は文字数×1文字あたりの情報量
(余談)ローマ字「ん」の後ろにbmpが来る場合、nではなくmで表記(ヘボン式)namba(なんば)
色の情報量
光の3原色・・RGBそれぞれ256階調とすると、一色8bit
3色で8×3で24bit
情報量はマス目(ピクセル)数×1マス(ピクセル)あたりの情報量
補助単位
補助単位はキリのいい数字・・・切りの良い数字とは?十進数の世界ち二進数の世界のキリのいい数字は異なる
十進数 10 二進数 1010
十進数 16 二進数 10000
K→M→G
十進数は1000
二進数は2^10=1024≒1000
キロ・・・kとK
音の情報量
空気の振動(粗密波)Hz
人間の可聴域は20Hz~20kHz
(余談)超音波とは可聴域を超えたところの週が数の音波・・・故に人には聞こえない(ハズ)
サンプリング周波数・・・どのぐらいの周期で音信号をひらっているか・・・CDは44.1kHz
情報量は音信号の情報量(16bit×2チャンネル=4bit)×1秒あたりのサンプリング数×曲の長さ(秒数)
(参考)なぜ650MBのCD-Rに74分の音楽が記録できるのでしょうか?
http://okwave.jp/qa/q2070273.html
第3回 情報学(Ⅲ)-ネットワーク技術について
到達目標3-1ネットワークにはどのようなものがあるか挙げることが出来る
3-2コンピューターネットワークの速度の計算が出来る
ネットワークとは
繋がり(ノードとエッジの関係)世の中には様々な繋がりがある
人間関係・・・様々な情報が集まる
(余談)私のブログ・・・弱いこともいいことだ(御卒業おめでとうございます)・・・当時の卒業生へのメッセージ
http://medbb.exblog.jp/19464438/
電話(音声通信)ネットワーク・・・無線化(携帯電話)により開発国で整備が進む
高速道路ネットワーク
航空ネットワーク・・・ハブ空港の存在
テレビ局ネットワーク・・・各系列が広範囲に情報を
(余談)腸捻転
https://ja.wikipedia.org/wiki/%E8%85%B8%E6%8D%BB%E8%BB%A
コンピューターネットワーク・・・様々な情報(文字・音・写真・音楽・映像)を流せる
インターネット・・・ネットワークとネットワークが繋がって形成(蜘蛛の巣状)・・・スケールフリーネットワーク →故障に強いが、攻撃には弱い
インターネット上で様々な(人的)ネットワークが作られている・・・LINE Facebook Twitter Mixi etc.
インターネットではプロトコル(規約)がある・・・電話だって「もしもし」
デジタルネットワークによる伝送
単位・・・bit/sec=bps計算問題いろいろ
第4回 情報学(Ⅳ)-情報セキュリティ
到達目標4-1情報セキュリティの定義(3要素)について説明出来る
4-2暗号化の必要性について説明できる
技術的な話が良く出てくるが、どうしても人が絡むところ(運用)が弱くなる
情報セキュリティ・・・情報の機密性、完全性、可用性の確保
http://www.soumu.go.jp/main_sosiki/joho_tsusin/security/intro/security/index.html
キーワード:ウイルス(普通のウイルスとの違い)https://ja.wikipedia.org/wiki/%E3%82%B3%E3%83%B3%E3%83%94%E3%83%A5%E3%83%BC%E3%82%BF%E3%82%A6%E3%82%A4%E3%83%AB%E3%82%B9、電子掲示板(普通の掲示板との違い)、SNS、脆弱性、認証、セキュリティポリシー
技術的な話
インターネットの世界は公共の場 → トンネル → 暗号化通信 例:SSL通信(https)平文→暗号文 暗号化
暗号文→平文 復号化
http://www.soumu.go.jp/main_sosiki/joho_tsusin/security/basic/structure/02.html
暗号の例
転置式暗号・・・文字の並べ替え
換字式暗号・・・ポリュビオスの暗号表・・・ポケベル
運用上の話
【資料】SNS時代における個人情報保護と情報セキュリティhttp://www.medbb.net/wiki/index.php?sp%2F20140829kosakawh
【資料】特別講義 漏洩と拡散の危機から情報を守る考え方
http://www.medbb.net/education/joho20150724/index.html
授業では触れませんが家で読んでおいてください
情報セキュリティ読本 教育用プレゼン資料(IPA) https://www.ipa.go.jp/security/publications/dokuhon/ppt.html
第5回 保健医療情報システム(Ⅰ)-医用画像について
到達目標5-1DICOM規格について説明できる
5-2画像検査の種類や特徴について説明できる
DICOM
医用画像のデジタル保存・伝送に関する規格 http://medical.nema.org/Dicom/about-DICOM.htmlデファクトスタンダード
http://e-words.jp/w/%E3%83%87%E3%83%95%E3%82%A1%E3%82%AF%E3%83%88%E3%82%B9%E3%82%BF%E3%83%B3%E3%83%80%E3%83%BC%E3%83%89.htmlQ.3つほど例を挙げよ
放射線を利用した画像について
被曝の話http://www.pet-net.jp/pet_img/treat/hibaku1.jpg Q.3つほど例を挙げよ
外部被曝と内部被曝の違い
X線写真
アナログからデジタルへ移行(銀塩写真→デジタルカメラ)反射光を記録するのではなく透過光を記録
物質により透過具合が違う
造影剤は画像の濃淡を増強させるため
画像を取得しながらそのまま治療 → IVR
愛知医科大学IVR 治療を受けることになりました。どのような治療ですか?
CT
デジタルだからこそなし得た画像横から見ているのに上から見た状況を推測
横断像が基本
MRI
強力な磁場の中で電磁波(ラジオ波)を利用。放射線を使わない。音
アクシデント 失敗百選 ~MRIにボンベが引き込まれて男児に衝突~
http://www.sydrose.com/case100/257/
様々な断面の情報を取得できる
核医学検査
放射性同位元素を体内に投与そこから出てくる放射線(γ線 PETは消滅放射線)を外側で検出
ガンマカメラ
γ線を検出して平面像を得る
SPECT
ガンマカメラのCT版
PET
陽電子放出核種を利用
超音波
音波を利用反射するまでの時間を距離に変換
内視鏡
国内機器メーカーが圧倒的シェア上記の医用画像との違いは、体の中を診るのに体外からアプローチしていたのを、体内に機械を放り込むところ
生検が可能
第6回 保健医療情報システム(Ⅱ)-電子カルテについて
到達目標6-1カルテに記載される情報について説明できる
6-2電子カルテの必要な要件について説明できる
6-3電子カルテの意義と問題点について説明できる
課題(任意)
カルテの作成義務や保存義務が無かったらどのような不具合が起こるか。自分の考えをまとめよ
カルテ
法令で「カルテ」なる言葉は出てこない。 「診療録」のことを指す
東京都衛生部 都立病院における診療録等記載マニュアル
http://www.byouin.metro.tokyo.jp/hokoku/guideline/documents/sinryoroku.pdf
配布資料は診療録等の定義と関連法規・記載の原則と留意事項(P1-P6)
・医師法<資格法>で作成や保存について定められている。
・治療に関すること以外の記載もある
電子カルテ
医療情報システムの安全管理に関するガイドライン第4.2 版(平成25年10月)厚生労働省http://www.mhlw.go.jp/file/05-Shingikai-12601000-Seisakutoukatsukan-Sanjikanshitsu_Shakaihoshoutantou/0000026087.pdf
配付資料はこの中の「7 電子保存の要求事項について」の部分(P81-P96)
法的に保存義務のある文書等の電子保存の要件
・真正性・見読性
・保存性
電子カルテの意義と問題点
新たな事が出来るようになると同時に、新たな事案も発生する(ゆえに、状況を把握し理解する力が必要)
・データ入力:手書き文字からの開放
・データ活用:情報の共有
・データ保存:データの紛失防止・長期保存
到達度確認
1)保険医が診療録に記載しなくてはならない情報をまとめよ2)電子カルテに必要な3用件をまとめよ
3)電子カルテのデータ保存に関する問題点を挙げ、その対策を考えよ
第7回 保健医療情報システム(Ⅲ)-施設内の情報システムについて
到達目標7-1病院内の情報システムにどのようなものがあるか説明できる
7-2オーダーエントリーシステムと電子カルテの情報の違いについて説明できる
7-3病院情報システムに求められる用件を説明できる
課題(任意)
病院内においてOTはどのような情報を記録していく必要があるか、そして施設内にあるどのような情報の活用が求められるか。自分の考えをまとめよ
参考資料 作業療法記録・報告文書の書き方 - 日本作業療法士協会
http://www.jaot.or.jp/wp-content/uploads/2010/08/practice-lecture-32-2.pdf
病院情報システム
HIS(Hospital Information System)狭義のHIS・・・オーダーエントリーシステム
広義のHIS・・・電子カルテも含めた病院全体のシステム
病院情報システムの発展の歴史
医事会計システム(レセコン=レセプトコンピュータ)がスタート(レセプト・・・診療報酬明細書)
医療機関からの請求も電子化が進む(リンクは社会保険診療報酬基金)
http://www.ssk.or.jp/rezept/files/hukyu01.pdf
配付資料は全ページ
オーダーエントリー・電子カルテ普及状況(JAHIS オーダリング電子カルテ導入調査報告 -2013年調査(平成25年))
http://www.jahis.jp/members/data_list/data0202/
配付資料は全ページ
発展の鍵は費用対効果?
医事会計電子化・・・デジタル加算(アナログ減算)
オーダーエントリー・・・コスト漏れが防げる
電子カルテ・・・?
オーダーエントリーシステムと電子カルテの機能の違い
オーダー伝達と結果参照の話電子カルテの定義に関する日本医療情報学会の見解(日本医療情報学会)
http://jami.jp/citizen/doc/eKarte.pdf
電子カルテの位置づけと機能のところがポイントだが配付資料は全ページ
PACS
Picture Archiving and Communication SystemDICOM規格の話
(画像の発生と転送時間の計算が出来るように)
病院情報システムに求められる用件
・処理の確実性システムが肥大化しており影響も広範囲に
・システムの頑健性
いまさら代替手段がない
・データの冗長化
無駄なように見えて無駄じゃない
・データの継続性
csv(Comma-Separated Values)に出来ればなんとかなる
・データの機密性
公的な性質を持つ情報システムほど機微な情報が集まる
・分かりやすい操作性
特別な教育がなくとも使える
・早いレスポンス
クライアント側で処理させるか、サーバーサイドで処理させるか、プリフェッチ(事前に読み込み)
・低コスト性
全体のコストで見ないと
システム運用のメリットデメリット
システム運用のメリット
情報伝達が迅速転帰や再入力が不要
閲覧様式が自在
正確な情報収集
検索・集計が容易
保存スペースが小さく長期保存可
情報へのアクセスが迅速
紛失リスクが少ない
紙運用のメリット
情報収集の柔軟性近くの人への情報伝達の手軽さ
真正性の確保(甘さ?)
運用変更への対応
情報の分散管理
到達度確認
1)部門を結ぶシステムについてそれぞれの役割をまとめよ2)オーダー伝達の情報があるにもかかわらず結果の情報の無い場合がある。どのような状況が想定されるか述べよ
3)病院情報システムに求められる用件の中でデータの蓄積に関わるものを挙げ、必要な理由を述べよ
第8回 保健医療情報システム(Ⅳ)-施設間の情報システムについて
到達目標8-1標準化に関する規格やコードや団体などについて説明できる
8-2遠隔医療の類型にどのようなものがあるか説明できる
8-3情報交換に必要な標準化に関する用語を理解できる
課題(任意)
SNSによって様々なPtoPの遠隔医療が実際に行われている。どのような事に注意しなくてはならないか自分の考えを述べよ
情報を共有するために避けられない標準化
5分でわかる「医療情報の標準化」(アイテック株式会社)http://www.itec-ltd.co.jp/wordpress/report/02.pdf
配布資料は全ページ
標準化・・・誰にでも理解できるように(故に情報は欠落するわけだが)
HL7 DICOM ICD-10などなど
医療情報システムの標準化についてのパンフレットをPDFにて公開いたします(JAHIS)
http://www.jahis.jp/2013/01/10/medinfosystem_brouche/
配布資料は医療情報システムの標準化について【Vol.1】および【Vol.2】の全体版
規格名などがたくさん出てくるが、何を担っているのか
遠隔医療システムの類型
DtoD(Telemedicine)
医療者対医療者一人の医療者が全ての専門知識を持っているわけでは無い
専門医制度
http://www.japan-senmon-i.jp/
テレラジオロジー(放射線科医による読影)(ビデオ)
テレパソロジー(病理医による病理診断)術中迅速診断
テレカンファレンス(他施設の医療者との症例検討)
DtoP(Telecare)
医療者対患者医師法第20条の解釈
PtoP
患者対患者Communication Network Analysis in Maternity Hospital Bulletin Board System
Journal of Medical Systems(31/2)141-148 Shunji Suto, Nobuyuki Ashida, Terumasa Higashi, Hideo Takemura, Koji Kurimoto and Shiro Yorifuji
図説・日本の遠隔医療2013(日本遠隔医療学会)
http://jtta.umin.jp/pdf/telemedicine/telemedicine_in_japan_20131015-2_jp.pdf
配付資料は 遠隔医療とは、遠隔医療の社会的背景、遠隔放射線画像診断(P2-P7,P9-P10)
到達度確認
1)ICDは日本国内においてどのような格好で利用されているかまとめよ2)DtoDの類型の遠隔医療にはどのようなものがるのか、なぜ必要なのかまとめよ
3)DtoPにおいて注意すべき点をまとめよ
第9回 統計基礎(Ⅰ)-尺度・度数分布について
到達目標9-1記述統計と推測統計について説明できる
9-24つの尺度について説明できる
9-3度数分布表が作成できる
課題(任意)
WHOからソーセージなどの加工肉の摂取ががんを発症する原因になるとの見解を発表して大騒ぎになりました。
ウインナーの買い控えなどが起こりましたが、今は落ち着きを取り戻しています(よね)
さて、発表直後に周囲の人が動揺しているときあなたは、周囲の人が落ち着くよう口頭で情報提供をしなくてはならなくなりました。
さてどのような説明をしますか?300~400字程度(口頭で約1分)のしゃべり(スピーチ)原稿を作ってみてください
参考記事:WHO発表の衝撃! 加工肉や赤身肉と、どう付き合うべき?(日経トレンディネット)
http://trendy.nikkeibp.co.jp/atcl/column/15/1054402/110600001/
参考記事:加工肉に発がん性?衝撃のWHO機関の研究報告 根拠は欧米での「聞き取り調査」(産経新聞-Yahoo)
http://headlines.yahoo.co.jp/hl?a=20151115-00000525-san-life
統計とは
私の考える統計学
『気づかせてくれるもの。うすうす気づいていることを確認するもの』私の考える医療統計学(2015)
『ある事象のなかで一般化出来るもの(法則性)を見いだすことは、その個別の事例にとどまらず広く利用できる知見をもたらす。そのためには複数の事例を集めて検討する統計処理が必要になる。それゆえ、統計処理は個別の事情を発生頻度により排除する主義に基づく。
私達の周りで起こる様々な事象は自然現象によるものだけではなく人間活動などの人工的な要因の影響を受けるものも多く、そのため法則性を見いだすにはそれぞれの領域の目的に応じた統計処理が必要となる。
医療統計学は、単に生物としてだけではなく活動状況も多様な集団である人に対して、提供する医療が及ぼす影響やその要因に関する法則性を見いだす方法を探求する学問分野である。』
(複雑なため確定的な事象はなく確率的に取り扱う必要がある)
統計の分類
記述統計と推測統計に分類される記述統計とは
・収集したデータを要約してその集団の状況を表す・そこにあるデータは全体(母集団)
・度数(分布)・代表値・散布度など
推測統計とは
事象の起こる確率を仮定した上で全体(過去・現在だけではなく未来も含む)を推測する。推定と検定に分類される。推定とは
・収集したデータを基にしてその集団の状況を表す・そこにあるデータは一部(標本)
・点推定・区間推定
検定とは(この領域の具体的な部分は2年次開講「統計学」にてエクセル使いながら)
・収集したデータを基にしてその集団の状況を仮定に従ってyes/Noで判断する・そこにあるデータは一部(標本)
・t検定・カイ二乗検定など
母集団とは
対象としている集団の全体を指し示すときに「母」を最初に付ける。無限母集団と有限母集団からなる。
対象が有限か無限に増殖するかの違い
標本とは
母集団の一部。昆虫標本を思い浮かべると、偏りに注意する必要があることは自明。
参考
標本調査はサンプル抽出が命(The Huffington Post Japan)http://www.huffingtonpost.jp/nissei-kisokenkyujyo/sample-survey_b_5878832.html
変量(データ)の分類
変量は様々なものがあるがそれらの性質をとりまとめ分類することが出来る。それぞれを尺度と呼び、4つに分類するのが一般的である
1名義尺度
2順序尺度
3間隔尺度
4比例尺度
1,2を質的変量(定性的)
3,4を量的変量(定量的)
性質としては上位互換性があり
4>3>2>1
度数分布表
それぞれのデータ(変量)の数(出現頻度)をまとめたもの変量が名義尺度の時は多い順(お作法として。但しその他を出すなら一番最後)
順序尺度以降であれば順(名義尺度でも比較のためにお作法を破ることはある)
度数 ・・・出現頻度
累積度数・・・上位の変量の度数もあわせた度数
相対度数・・・総出現頻度を1(100%)としたときのそのぞれの度数のしめる割合
累積相対度数・・・累積度数の相対版
度数分布図
度数分布表をグラフ化したもの縦棒グラフだが量的変量に限っては「ヒストグラム」その棒の部分の面積が度数を示している
スタージェスの公式
量的変量の度数分布表・図作成の時に階級幅設定の参考になる公式K(階級数)=1+log2(サンプル数)
今回の配付資料のサンプル数は50なので
1+5.64=6.64
7ぐらいが適当
上記を参考にしながら階級幅を決めるとよい(かも程度で)
参考:ヒストグラムは怖い-スタージェスの公式(高校数学の問題を作る -工夫・コツとデータ- )
http://www10.plala.or.jp/mondai/columun/hist.pdf
(経験則に基づいたものだとばかり思っていたのでビックリ)
到達度確認
1)記述統計と推測統計についてまとめよ2)4つの尺度についてそれぞれの変量の例をあげ説明せよ
3)配布した血液検査データのRBCについて度数分布表・度数分布図を作成せよ
第10回 統計基礎(Ⅱ)-代表値について
到達目標10-1代表値にどのようなものがあるか説明・計算することが出来る
10-2度数分布表から平均値などの算出が出来る
課題(任意)
「平均的○×」と自分を比較するとなんとなく安心したり、不安になったりしませんか
授業では代表値としてその他のものも学習しましたがなかなか使われません。
そこで、自身が生活していく上で使っている平均値,中央値,最頻値をそれぞれ挙げてみてください。
その上で、なぜ人は平均値を使ってしまうのかその理由を考えてみてください。
代表値と散布度があると(構成数nもですが)その集団がどんなものか想像出来る(マラソン実況)
代表値
average(その集団を数値一つで表す。excelはaverage関数で算術平均を出すが、まぁ代表値の代表ということだからと解釈しています)算術平均
mean(算術平均以外にも相乗平均(積して累乗根をとる)などもあります)1/n・Σxi
正社員男性の平均給与「527万円」 引き上げているのは誰なのか?(BLOGOS-キャリコネニュース2014年10月04日)
http://blogos.com/article/95831/
中央値
median(別名第二四分位数)量的変量を順序尺度で処理した代表値
順番に並べたとき真ん中の順位にきた個体の値
個体数が偶数の時は真ん中2つの数値の平均値
スキージャンプの飛型点は中央値的なノリで算術平均している
スキージャンプを知ろう!!ルール解説(ジャンプ雪印メグミルク)
https://www.meg-snow.com/jump/rule/rule.html
最頻値
mode(流行,はやり)違う意味で数の理論(多数決)の世界
量的変量を名義尺度で処理した代表値
名義尺度でわかることは一緒か違うか
階級毎に度数をカウント
一番多いところの階級値
一位が同点の時は併記(平均をとると えっオレ優勝!?状態になる)
度数分布表から算術平均を計算
Σ(階級値×度数)/構成数
到達度確認
1)外れ値の影響を受けやすい代表値を示し理由を説明せよ2)前回配布した血液検査データのRBCについて代表値をそれぞれ求め、前回作成の度数分布表より平均値を概算せよ
第11回 統計基礎(Ⅲ)-散布度について
到達目標11-1散布度にどのようなものがあるか説明・計算することが出来る
課題(任意)
購入した製品が不良品だったことはありませんか?
歩留まり率は期待される生産量と実際に作られた生産量(但し良品)の比率を求めたもので高ければ高いほど良い。
例えば食品であれば充填量のバラツキを抑えていくことで歩留まり率を向上させることが出来る
医療においても、質を向上するにあたりさまざまな「バラツキ」と向き合っていかなくてはなりません
一医療者としての視点でも結構です、病院全体を管理する視点でも、医療圏全体を管理する視点でも結構です。
あなたは、医療の質の向上に向かってどのようなバラツキと向き合い、解決していくのでしょうか?
散布度・・・dispersion
最大値と最小値を使う
最大値と最小値がわかればその集団のバラツキがわかる最大値maximum excel max関数
最小値minimum excel min関数
範囲
RangeR=最大値-最小値
特徴
外れ値もひらう
算出が用意
四分位数を使う
Quartile小さい順(昇順)に並べて集団を4分割
第1四分位数 First Quartile:Q1 = 25th percentile 25%タイル値
第2四分位数 Second Quartile:Q2 = 50th percentile 50%タイル値 = Median 中央値
第3四分位数 Third Quartile:Q3 = 75th percentile 75%タイル値
四分位数の求め方・・・厳密には数種類ある
授業では簡易に求められるヒンジ値を使用
参考記事 ダンゴ包丁理論(MedBBexblog)
http://medbb.exblog.jp/12047409/
四分位範囲
IQR(interquartile range)IQR=Q3-Q1
四分位偏差
QD(Quartile Deviation)QD=IQR/2
範囲は個々の値のバラツキをイメージ
偏差はある値からのズレをイメージ
平均値を使う
mean偏差
Deviationもともとは標準となる数値からのズレ(偏り)を意味するものだが統計の世界では集団の平均値からのズレを示す
偏差の平均をとれば集団内の各々のズレっぷりがわかる → 合計は常に0 故に平均も常に0
分散
varianceV excel関数はVAR
偏差の二乗したものの平均
標準偏差
Standard Deviation記号は標本s 母集団σ
s=√V
(故にVはs^2やσ^2で表現する)
到達度確認
1)前回配布した血液検査データのRBCについて散布度をそれぞれ求めよ(No.1-10迄のデータで)第12回 医療統計(Ⅰ)-病院の統計資料
医療を提供することで発生するデータのとりまとめる到達目標
12-1統計資料にどのようなものがあるか説明・計算・情報収集をすることが出来る
12-2既存の資料から必要なデータを抽出することが出来る
課題(任意)
例えばレコーディングダイエットのように、データを蓄積し可視化することで問題意識を持ち改善されるケースがあります。
しかしながら過度なダイエットは健康を害するおそれもあります。
あなたの友人がレコーディングダイエットをしようとしているとき、あなたはどのような助言をしますか?
運営上必要なもの
医療費の請求出来高払い
レセプト(診療報酬明細書)http://www.ssk.or.jp/yoshiki/yoshiki_05.html
DPC/PDPS
http://www.igaku-shoin.co.jp/paperDetail.do?id=PA02930_03義務に基づくもの
・医療施設調査(医療施設調査規則)http://www.mhlw.go.jp/toukei/list/79-1.html
静態調査と動態調査に分かれる
・病院報告(統計法に基づく一般統計調査 医療法施行令)
http://www.mhlw.go.jp/toukei/list/80-1.html
・患者調査(統計法に基づく基幹統計)
http://www.mhlw.go.jp/toukei/list/10-20.html
一月分(9月)のデータ
届出上必要なもの
施設基準の届出https://kouseikyoku.mhlw.go.jp/kantoshinetsu/shinsei/shido_kansa/shitei_kijun/tokukei_shinryo.html
経営管理上必要なもの
人件費率 など(ちなみに病院の場合50~60% うち医師で12~15%ぐらい)様々な調査データとの比較
例)病院経営管理指標
http://www.mhlw.go.jp/topics/bukyoku/isei/igyou/igyoukeiei/kannri.html
病床規模であったり開設母体別であったり
医療機能を評価する上で必要なもの
平均在院患者数
一泊二日を入院日数2日と数えている平均外来患者数
平均在院患者数の日数と違い診療日で除する平均在院日数
入退院データから算出する方法と、患者票の「入院年月日」と「退院年月日」から直接差引き計算により在院日数を求める方法がある平均病床利用率
100%が良いというわけでもない病床回転率
平均在院日数と関係する死亡率
低い方が望ましいが、単純に比較してはならない新生児死亡率
出生数あたり参考
厚生労働統計に用いる主な比率及び用語の解説http://www.mhlw.go.jp/toukei/kaisetu/index-hw.html
奈良県立医科大学 概要
http://www.naramed-u.ac.jp/university/gaiyo/shokai/gaiyo.html
配付資料は平成27年度のP49(第6章附属病院)-P57まで,P63(リハビリテーション関係)
到達度確認
1)奈良医大の各診療科別及の外来/入院比率を求めよ(指定の年度について)2)150床の病院で新入院患者が3000名退院患者が2400名だった。延在院患者数が40000名だった場合の平均在院日数を求めよ
3) 2)の条件における病床回転率を求めよ。また年間平均病床利用率も求めよ
4)同一機関における粗死亡率と精死亡率を比較したとき、どちらが高くなるか。その理由も述べよ
第13回 医療統計(Ⅱ)-比と率と割合
医療を提供することで発生するデータのとりまとめる到達目標
13-1比と率と割合について説明できる
13-2人年法について説明や計算が出来る
課題(任意)
比
ratio異なるもので割ったもの・・・単位は無次元の場合もある
例)BMI(Body Mass Index)
身長の二乗(m^2)に対する体重(kg)の比
身長170cmで体重70kgの人のBMI・・・70/(1.7^2)≒24.2
検査表の見方(日本人間ドック学会)
http://www.ningen-dock.jp/public/method
率
rate時間に対する何かの量の比・・・単位は無次元の場合もある
変化を表す指標
例)時速
マラソン(42.195km)を2時間6分で走った場合の時速・・・42.195/2.1≒20.1km/h
100m走を10秒で走った場合の時速・・・0.1/(10/3600)=36km/h
無次元の例としては稼働率
稼働率(JIT基本用語集)
http://www.lean-manufacturing-japan.jp/jit/cat241/post-74.html
時間を時間で割るので無次元
割合(比率)
proportion全体に対してその一部がどの程度占めるか割ったもの・・・単位は無次元になる
0~1の間の値をとるpercentで表示したりする。100%を超えるのは本来おかしい
例)日本人の血液型の割合
A型 約40%
B型 約20%
O型 約30%
AB型 約10%
人年法
一人の人を一年観察したとき1人年人年に対する何かの量の比・・・率になる
例)5人の患者を1年間観察していた時に二人死亡
Aさん 1年後生存
Bさん 3ヶ月後に死亡
Cさん 9ヶ月後に死亡
Dさん 1年後生存
Eさん 1年後生存
<本来の死亡率算出>
観察人年=1+0.25+0.75+1+1=4人年
その間の死亡数が2なので
2/4=0.5 「1人年対0.5の死亡率」
<年央人口を用いる方法だと>
6ヶ月経過の時点での生存者4人
1年経過後の集団の死亡数が2なので
2/4=0.5 「1人年対0.5の死亡率」
<参考>
http://www.mhlw.go.jp/toukei/kaisetu/index-hw.html
到達度確認
1)比,率,割合のいずれか示せ円周率
打率
時速
出生性比=(年間の男子出生数/年間の女子出生数) ×100
大学進学率=大学(短期大学含む)入学者数÷3年前の中学卒業者数
2)
年間婚姻届出件数 ×1,000
婚姻率= ――――――――――――
10月1日現在日本人人口
である。割合ではなく率である理由を述べよ
第14回 医療統計(Ⅲ)-相対危険度
どれだけ危険になるのか?効果があるのか?を知る指標Relative Risk
到達目標
14-1相対危険度を示す指標にどのようなものがあるか説明できる
14-2状況に応じて適切な相対危険度を示す指標を選択できる
この授業では相対危険度=Relative Risk は一般的な用語であり、その算出指標の一つに相対危険=リスク比(Risk Ratio)があると整理します
一般的にはここらへんの言葉ゴチャゴチャです。
説明用データ
| 疾病発症 | 疾病無 | 計 | |
|---|---|---|---|
| 曝露有 | A | B | A+B |
| 曝露無 | C | D | C+D |
| 計 | A+C | B+D |
相対危険
Risk Ratio(RR)「リスク比」と言った方がわかりよい(と思うが)
曝露(介入)の有る時と無の時の危険を示す指標の比
危険を示す指標には罹患率やら有病率やら死亡率やら
A~D:疾病発生頻度(頻度以外に罹患率やら有病率・・・)
曝露有群の発症リスク=A/(A+B)
曝露無群の発症リスク=C/(C+D)
リスク比=A/(A+B)/C/(C+D)
もし、発生頻度が低ければA+B≒B C+D≒D
リスク比≒A/B/B/D=AD/BC
----------
<参考>寄与危険
Attributeable Risk
相対危険は関係性(比で関係性を見る)
寄与危険は影響の大きさ(差でインパクトを見る)
リスク差(Risk Difference)=A/(A+B)-C/(C+D)
----------
オッズ比
Odds Ratio(OR)「リスク比」を出せない場合でも出せる(リスク比はそれぞれの群のリスクがわかっていないと出せない)
危険な事象が起きた場合と起きなかった場合度数の比(=オッズ)について曝露(介入)の有無毎に求め比をとったもの
発症有群の曝露オッズ=A/C
発症無群の曝露オッズ=B/D
オッズ比=A/C/B/D
=AD/BC
上記のように発症頻度が低ければオッズ比とリスク比の近似値となる
前向き(コホート研究)と後ろ向き(症例対照研究)
同じものを眺めるとき向きが違うとスタート地点も変わってしまう因果関係を観察する場合は時間軸が必ず必要・・・時間の世界で前後ろの話
(後ろ向きの場合は既に罹患しているわけで。疾病発症を症例群 疾病無を対照群と読替えて)
前向きの場合:スタート時点では正確な情報を集められるがゴールでは・・・
前向きの場合:結果=発症リスク
後向きの場合:スタート時点では正確な情報を集められるが遡ると記憶が・・・
後向きの場合:結果≠発症リスク
到達度確認
以下は空想の世界のお話し健康に気を使っているA食堂と、満腹感を優先するB食堂がある
それぞれの食堂で食した人が1年間利用して肥満体になったのか調査を行った。
コホートと症例対照研究両方で行っていたものとする。
それぞれリスク比とオッズ比を求めよ
結果より、どのような場合にリスク比とオッズ比は近似値となるか考察せよ
コホート研究
| 肥満 | 正常 | 計 | |
|---|---|---|---|
| A食堂 | 100 | 900 | 1000 |
| B食堂 | 50 | 950 | 1000 |
| 計 | 150 | 1850 |
| 肥満 | 正常 | 計 | |
|---|---|---|---|
| A食堂 | 100 | 72 | 172 |
| B食堂 | 50 | 76 | 126 |
| 計 | 150 | 148 |