�ޗnj�����ȑ�w�@�������v�w�Q�O�P�V
�i��w����w�ȁj
�{���Ƃ̈ʒu�t��
��w���烂�f���E�R�A�E�J���L�������i����28�N�x�����Łj���x�[�X�ɍ\��http://www.mext.go.jp/b_menu/shingi/chousa/koutou/033-2/toushin/1383962.htm
�{�u�`����w���烂�f���E�R�A�E�J���L�������ɂ����ĒS�������E��Ɋ֘A���镔��
B�Љ�ƈ�w�E���
�@B-1 �W�c�ɑ�����
�@�@B-1-1) ���v�̊�b
�@�@�@�m���ɂ͕p�x�ƐM�O�̓x�����̓������A�����p�������v�E���v�w�̗L�p���ƌ��E�𗝉����A�m���ϐ��Ƃ��̕��z�A���v�I�����i����ƌ���j�̌����ƕ��@�𗝉�����B
�@�@B-1-2) ���v��@�̓K�p
�@�@�@��w�A�����w�ł悭��������W�{�ɓ��v��@��K�p����Ƃ��ɐ�������_�A���v�p�b�P�[�W�̗��p���܂߂���̓I�Ȉ��������C������B
�@�@B-1-4) �u�w�Ɨ\�h��w
�@�@�@�ی����v�̈Ӌ`�ƌ���A�u�w�Ƃ��̉��p�A���a�̗\�h�ɂ��Ċw�ԁB
�@�@B-1-7) �n���ÁE�n��ی�
�@�@�@�n���ÁE�n��ی��݂̍���ƌ���y�щۑ�𗝉����A�n���Âɍv�����邽�߂̔\�͂��l������B
�@�@
���ƃ��j���[
��1��@�I���G���e�[�V����
��2��@�ړx�E�x�����z
��3��@��\�l�E�U�z�x
��4��@���ϒl�̐���
��5��@���W���E��A����
��6��@���x�E���ٓx�EROC�Ȑ�
��7��@���Ί댯�x
��8��@����̌���
��9��@�p�����g���b�N����
��10��@�m���p�����g���b�N����
��11��@�v���l�f�[�^�̌���
��12��@�Ɨ����Q�Ԃ̔�r
��13��@�������ԕ���
��14��@���ϗʉ��
��15��@�܂Ƃ�
13���14������ʂ̎���œ���ւ��Ă���܂�
��1��@�I���G���e�[�V����
���B�ڕW�P�|�P���Ƃ̊T�v������ł���
�P�|�Q���v�̎�ނɂ��Đ����ł���
�{���Ƃ̖ړI
�@�������v�w�́A���v�I��@��p���ĕی���Õ���ɂ�����ۑ�̉����Ɏ�����w��̈�ł���B���̂��ߓ��v�w�̊�b�����ł͂Ȃ��A����܂Ŗ{����ɂ����Ăǂ̂悤�ȓ��v�I��@���p�����Ă����̂��������A�f�[�^�̎��W�E��́E���߂����{����ۂɍœK�Ȏ�@��I�����邽�߂̒m���ƁA��������p����\�͂̊l����ړI�Ƃ���B
�{���Ƃ̓��B�ڕW
�P�j�f�[�^�̐����Ɋւ��Đ����ł����Q�j�K�ȓ��v��@��I���ł���
�R�j�����̓��v�w�I����@������ł���
�S�j�����f�U�C�����̓����ƃf�[�^����舵����ł̒��ӓ_������ł���
�O�j���v��@�ȂǕK�v�ɉ����āu������Ώo����悤�ɂȂ�\�́v���l������
���ȏ�
�V�œ��v�w�̊�b ��2�Łi��N�x�̎w�苳�ȏ��̉����Łjhttp://www.nikkyoken.com/catalog/catalog_education/642
�Q�l�}��
�o�C�I�T�C�G���X�̓��v�w�|���������p���邽�߂̎��H���_http://www.nankodo.co.jp/g/g9784524220366/
�Q�l����
�K�v�ɉ����ēK�X�z�z���܂����E�E�E���Ƃ̐i�ߕ�
�d��g���܂��̂ł�낵�����肢���܂��i���ƒ��̓X�}�z�ł��܂��܂������̎��́~�j
�P�ʔF��
����u���B�x�m�F�v�����{���܂��B��o�������������͕̂ԋp���܂��B��������ł͓d�엘�p���܂�
�u���B�x�m�F�v�͐���ɂ���ĕ]��������̂ł͂���܂���B�ŏI�I�ɐ������m���Ă������Ƃ��ړI�ł��̂ŊԈႢ������]�����Ȃ����Ƃ͂���܂���B
���v�����ɂ���
�W�c����f�[�^���Ƃ�܂Ƃ߂Ď����̂ŁE�E�E�y���v�w01�z�ϗʂ͑Ώۂ����鎋�_�B���_��ς��邱�ƂňႤ���̂������Ă���B���v�����͌ʂ̎����r������Ȃ����́B���ړx�̓}�C�i�X�̐��E���Ȃ��B�}���\����w�`�̐擪�W�c�͑�\�l�ƎU�z�x�Ŏ��������
— �߂ǂԂ� (@medbb) 2014�N9��24��

�i�f�[�^���͂���l����n���Ẩۑ��@���j
�m���ɂ���
�p�x�E�E�E�E�E�E�E�q�ϊm���E�E�E���g�̎v�l�ƂȂ��W�Ȃ��B���ۂ��O���璭�߂��i�p�x�𐔂����j�ߋ��̌��ʂŐl�ɂ��قȂ�Ȃ��M�O�̓x�����E�E�E��ϊm���E�E�E�����_�ł̎��g�̒m���ɂ�鐄�_�Ɋ�Â��E�E�E�_���I�i�Ȃ͂��j�����l�ɂ��قȂ�i�\��������j
�u�����I�ȏo�����́A��ϊm�����A�q�ϊm�������傫��������A�����������肷��v
���p���F��ϊm���̑傫���͂ǂꂮ�炢���|���̏o�����́A�{���Ɋ�ՓI�ƌ����邩?�F�������̊�iTHE HUFFINGTON POST�j
http://www.huffingtonpost.jp/nissei-kisokenkyujyo/odds_b_8965176.html
�Ƃ���ň�Â͈�Ï]���҂ɂƂ��ē��킾���A�Z���̕��ɂƂ��Ă͔����

�i�n��ƈ�Â̓����Ɏ����� ��p�̍l���� �|�s���̊ϓ_����݂���2.10�|�@���j
�̂Ɋ��҂���𒆐S�Ƃ����Ã`�[�����ŌX�̎�ϊm�����قȂ�Ɋׂ邩���B
�����e�B�z�[���W�����}
�R�̔�������܂��B��̔��Ƀn���C���s�B���Ƃ̓�͂��킵�������Ă��܂��B���Ȃ��͔�����I�т܂��B
���Ȃ��̑I�����n���C���s�̋q�ϊm���́H
�i��ҁi�j�O�Z�t���j���I���̂ƈႤ����������܂����B���킵�������Ă��܂����B
�Q�l�F�V����������Ⴂ�I�i�`�a�b���������j
http://www.asahi.co.jp/shinkon/
���Ȃ��̑I�����n���C���s�̎�ϊm���́H
�@�t���͂��킵�ƒm���ĂĂ������ꍇ�i���Ȃ������ł��邱�Ƃ�m���Ă���j
�@�t���̓n���C���s���o���Ă����܂�Ȃ��Ǝv���Ă������ꍇ�i�ԑg�Ƃ��Ă͂Ԃ����������������Ƃ����邱�Ƃ����Ȃ��͒m���Ă���j
���ۂɊF����ܕi�����ĂĂ݂܂��傤
�ܕi�͈�B�c��̓�̓n�Y��
�P�D3�̔��iA�@B�@C�j��I��ł��������B�I����A�Ƃ��܂�
�Q�D����B,C�̔��̒�����n�Y���Ă���i���Ƃ�m���Ă���j��B���J���܂�
�R�D�c���A��C�ς��邱�Ƃł��܂����ǂ���ɂ��܂��H���B�x�m�F�̖��P�j
�ł́A���ۂɂǂ�Ȃ��̂����Ă݂܂��傤
�l�R�ł��킩�郂���e�B�z�[���W�����}(DOFI-BLOG �ǂӂ��Ԃ낮)
�L�q���v�Ɛ������v
���v�Ƃ͂Q�ȏ�̗v�f�̏W�܂肩��Ȃ�W�c�̓����𖾂炩�ɂ��邱���W�c�̓������X�̓����@�Ƃ����l�����B���ۂɂ́@�W�c�̓������X�̓����@�̃P�[�X������
�L�q���v�w
�f�[�^�̏W�c�����������̂��i��舵���f�[�^���S�āj�x�����z�E��\�l�E�U�z�x
�������v�w
����ƌ���ɕ�������ǂ������舵���f�[�^�͖��炩�ɂ������S�̂̈ꕔ���ƂȂ�
����
�f�[�^�����������̂��@�ꕔ�̃f�[�^��Ώہ@ ���@�S�̂𐄑�
����
�f�[�^���ǂ̂悤�ȏ��@�^����ꂽ�f�[�^��Ώہ@���@���E�E�E�����\��
���҂͖��ڂɊ֘A���Ă���
���B�x�m�F
�P�j�c���A��C�ς��邱�Ƃł��܂����ǂ���ɂ��܂��H�Q�j���v�����Ȃ��̐l���ɍK���������炷�\���̒��x�i�m���j�������A���킹�Ă��̗��R���q�ׂ�
���ƌ�⑫
�����e�B�z�[���W�����}�ƐV����������Ⴂ�I�V����������Ⴂ�I�͎����̈�t�Ŕ���I�Ԃ̂ł͂Ȃ������őI��ł܂��������e�B�z�[���W�����}�⑫�����e�B�z�[���ł����[���ł��Ȃ��ꍇ�̓g�[�i�����g��ŗD������`�[���̗\�����l����Ɨǂ���������܂��� ���ꂼ��̃`�[���̃��x�����킩��Ȃ����������ŃV�[�h�����߂��Ƃ������J�n�O �D������m���@�V�[�h�ɊW�Ȃ��S�ā@1/9��11%1���I�����_ �E�������`�[���͎��͂ł͂Ȃ��c�C�Ă邾���Ƃ����ꍇ �g�[�i�����g�c���4�l+1�l�Ȃ̂ł��ꂼ��ϓ����i�Q�O���j �E�������`�[���͎��͂��ؖ������ƍl����ꍇ �g�[�i�����g���͎����Ŏc����4�l�͗D���̊m�����オ�邪�A�V�[�h���͉������Ă��Ȃ��̂ł��̂܂� ������ �E�������`�[���͎��͂ł͂Ȃ��c�C�Ă邾���Ƃ����ꍇ �g�[�i�����g�������c���Ă������ƃV�[�h���Ɏ��͂̍������邩�킩���Ă��Ȃ��̂ł��ꂼ��D������m����50% �i�V�[�h�͉������Ă��Ȃ��̂ɏ���ɗD���m�����オ��j �E�������`�[���͎��͂��ؖ������ƍl����ꍇ �g�[�i�����g�������c���Ă������ƃV�[�h���Ɏ��͂̍�������\��������B�V�[�h�̗D������m����11%�̂܂܂Ȃ̂Ńg�[�i�����g�������c�����ق���89% �i���F�����ł̔�ꂪ���̎����ɋ����Ȃ����O��ƂȂ�܂����j �����ƌ����̈Ⴂ�̘b���v���o�����肵�Ă��܂����B �V�[�h�����鎞�_�Ō����ł͂Ȃ��Ƃ��Ă��A���ꂪ�����ł��邱�Ƃ�ے肷����̂ł͂Ȃ� �t�Ɍ����ł���Ό����Ƃ͌���Ȃ� �W�ꂽ�f�[�^���猩��ƌX�̎�����������Ă��镪�A�����ł���Ό������낤�ƂȂ�B�̂Ɍ����ɂ������̂ł��傤�B �X�̃f�[�^�J�ɂ݂�ƌX�̏��݂��Ă��āA�����ł͂Ȃ��Ƃ������� �����͋@����ϓ��ɁB�����͌��ʂ���c�L�i�o���c�L�j����菜���B �ʏ�̓`�[���̎��͂��ӂ݂Č����ł͂Ȃ��Ƃ������ȕ����Ŏ�����g��ł��܂��B���Q�l���y�l�b�g�Řb��z�o�X�P�̐É������������^wwwww�y�^���z �iNAVER�܂Ƃ߁j https://matome.naver.jp/odai/2138278173194681601 ���̘b�͂��ꂩ��̒n��̕ی���Â̘b�ɕK�v�Șb�ł��B�ȑO���̂悤�Șb�������̂łǂ��� �n��ƈ�Â̓����Ɏ����� ��p�̍l���� �|�s���̊ϓ_����݂���2.10�| ���B�x�m�F�̂��ꂱ���P�j�i�ܕi�Ă邱�Ƃ��O��Ȃ̂Łj�ς���C��I�ԁi�ق����m���͏オ��j�@�܂����i���o�Ă��Ȃ��ꍇ�A�Ӑ}���ĂȂ�������AC�Ƃ���50%�����Ӑ}���Ă����ꍇA��33%�@B��66%�B�Ӑ}���Ă���\����ے�ł��Ȃ�����ς����ق����オ�� �Q�j50%�Ƃ����������������̂͂����炷�^�����炳�Ȃ��̓���ōl���Ă�����������������炩�ȁH  |
��2��@�ړx�E�x�����z
���B�ڕW�Q�|�P�f�[�^�̎ړx���ށi�S�̎ړx�j�ɂ��Đ����ł���
�Q�|�Q�x�����z�\���쐬�ł���
��W�c�Ƃ�
�ΏۂƂ��Ă���W�c�̑S�̂��w�������Ƃ��Ɂu��v���ŏ��ɕt����B������W�c�ƗL����W�c����Ȃ�B
�Ώۂ��L���������ɑ��B���邩�̈Ⴂ
�W�{�Ƃ�
��W�c�̈ꕔ�B�����W�{���v�������ׂ�ƁA��ɒ��ӂ���K�v�����邱�Ƃ͎����B
�����s�̐l���i�����s�j
http://www.city.kashihara.nara.jp/kikaku/toukei/jinkou/tikubetu_tyoubetu_jinkou.html
�e�n��ɂ���ĈقȂ�i�N��\�������Z���Ԃ��j
����26�N�o�σZ���T�X-��b�����i�m��j�ޗnj����ʕ���29�N3���i�ޗnj��j
http://www.pref.nara.jp/secure/67732/H26kakuho_gaiyo.pdf
�S���Ɣ�r���č\���䗦���قȂ邱�Ƃ͕����邪�S���̒��ł���w�W����ԂɂȂ�Ηǂ����ɂȂ�킯�ł��Ȃ�
�����܂ł��A�����Ă�����_�ƏƂ炵���킹�邱�Ƃŏ��݂��Ă���B
�ϗ�(�f�[�^)�̕���
�ϗʂ͗l�X�Ȃ��̂����邪�����̐������Ƃ�܂Ƃߕ��ނ��邱�Ƃ��o����B���ꂼ����ړx�ƌĂсA4�ɕ��ނ���̂���ʓI�ł���
�P���ގړx�i���`�ړx�j
�Q�����ړx
�R�Ԋu�ړx
�S��ړx�i���j
�P�C�Q�����I�ϗʁi�萫�I�j
�R�C�S��ʓI�ϗʁi��ʓI�j
�����Ƃ��Ă͏�ʌ݊���������
�S���R���Q���P
���ȏ��͊Ԋu�ړx�y�є�ړx�Ɋւ��ē��v�������ʂ���Ӗ��͖����ƂȂ��Ă��邪�A���ӂ͕K�v
�|�C���g�͐��w�I�ɂ͐����������Ƃ��Ă��Ӗ��I�ɐ��������ǂ���
�x�����z�\
���ꂼ��̃f�[�^�i�ϗʁj�̐��i�o���p�x�j���܂Ƃ߂������ϗʂ����`�ړx�̎��͑������i����@�Ƃ��āB�A�����̑����o���Ȃ��ԍŌ�j
�����ړx�ȍ~�ł���Ώ��i���`�ړx�ł���r�̂��߂ɂ���@��j�邱�Ƃ͂���j
�x���@�@�E�E�E�o���p�x
���Γx���E�E�E���o���p�x��1�i100%�j�Ƃ����Ƃ��ɁA���ꂼ��̓x�������߂銄��
�ݐϓx���E�E�E��ʂ̕ϗʂ̓x�������킹���x��
�ݐϑ��Γx���E�E�E�ݐϓx���̑��Δ�
�x�����z�\����Z�p���ς��v�Z�ł���
���i�K���l�~�x���j�^�\����
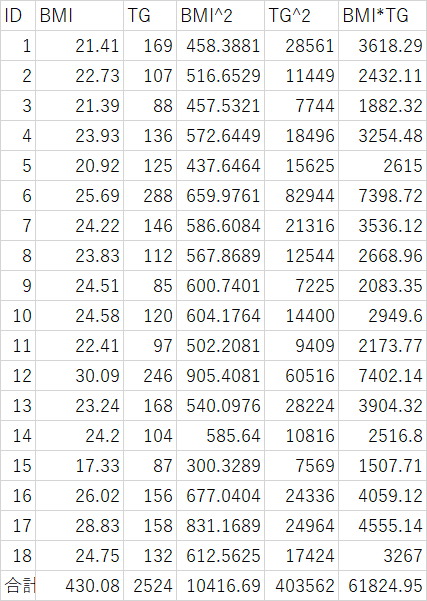
���ȏ�P11�́u���G�Ȓ����f�[�^�vTG�̓x�����z�\���쐬���Ă�������
���Q�l�� �g���O���Z���h�i�s�f�F�������b�j�\���b�̎听���A�얞�̎w�W�\�i���v���c�@�l �_�ސ쌧�\�h��w����j
http://www.yobouigaku-kanagawa.or.jp/kensa/kensati09.html
| �K�� | �K���l | �x�� | ���Γx�� | �ݐϓx�� | �ݐϑ��Γx�� |
|---|---|---|---|---|---|
| 75�`100 | 87.5 | ||||
| 100�`125 | |||||
| 125�`150 | |||||
| 150�`175 | |||||
| 175�`200 | |||||
| 200�`225 | |||||
| 225�`250 | |||||
| 250�`275 | |||||
| 275�`300 | |||||
| �v | ----- | 18 | 1.00 | ----- | ----- |
�x�����z�}
�x�����z���c�_�O���t�Ŏ����������ʓI�ϗʂ̏ꍇ�u�q�X�g�O�����v���c�_�̊Ԋu�͖����i�ʂ�����j
�_�O���t�̖ʐς����̓x���̗ʂ������B�����镔�������K������{�ɂ����ꍇ�x���͔����ŕ`��
���B�x�m�F
�P�j��L�̓x�����z�\�������������Q�j��L�̃q�X�g�O�������쐬����
�@�@������200�ȏ�̊K�����͂T�O�ō쐬�̎�
���ƌ�⑫
|
���ȏ��Y���y�[�W ��1�́iP10-P18�j ��2�́iP20,P29�j ���v�f�[�^�͕��L�������ق����ǂ����낤�Ƃ����̂��Ⴆ�ΎY�ƂƎ����̘b�B ���Q�l���U����Q�i���݂˂��ʐMNo.116����21�N2�����@�X�J�Еa�@�j http://www.aomorih.johas.go.jp/guide/umineko/2009/2.php �����Q�V�N�x�ޗnj��ыƓ��v http://www.pref.nara.jp/23014.htm �ыƘJ�� http://www.pref.nara.jp/secure/60021/11.roudou_h27.pdf ������]���҂̌���������킩��i����̃s�[�N�͉߂������j �����ƌ����̘b�B�w�W��S����r���ĈႤ�i�X�R�A���Ⴂ�j������P���K�v�@�������̓X�R�A����������������g�݂͕s�v�ƒP���ɍl����̂͂܂����Ƃ����b�B |
��3��@��\�l�E�U�z�x
���B�ڕW�R�|�P��\�l�̎Z�o�y�ѓ����ɂ��Đ����ł���
�R�|�Q�U�z�x�̎Z�o�y�ѓ����ɂ��Đ����ł���
��\�l�ƎU�z�x�Ƒ傫��n�i���⎖�ې��j�������A���̏W�c���ǂ�Ȃ��̂��z���o����i�}���\�������j
��\�l
average�i���̏W�c�𐔒l��ŕ\���Bexcel��average���ŎZ�p���ς��o�����A��\�l�̑�\�Ƃ������Ƃ�����Ɖ��߂��Ă��܂��j�Z�p����
mean�i�Z�p���ψȊO�ɂ����敽�ρi�ς��ėݏ捪���Ƃ�j�Ȃǂ�����܂��j1/n�E��xi
�p���[�g�̖@���i80-20�̖@���j
��\�l�Ȃ̂Ɏ��݂��Ȃ��ꍇ������@���@�W�c�̎w�W�i�d�S�j�ł����āA���ۂ��\����l���̂��̂������Ă���Ƃ͌���Ȃ�
��蓹
���ԋ��^���ԓ��v2015�i���Œ��jhttp://www.e-stat.go.jp/SG1/estat/GL08020103.do?_toGL08020103_&listID=000001159883&requestSender=dsearch
��9�\�@�Ǝ�ʋy�ы��^�K���ʂ̋��^�����Ґ��E���^�z ��� ���[�����c�Ȑ�
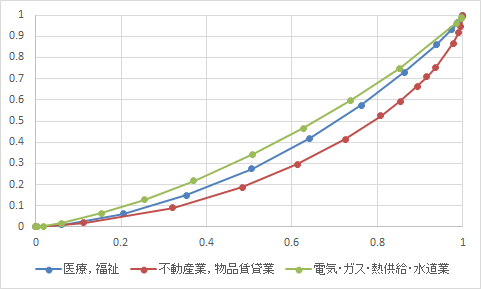
�W�j�W���͈�ÁC����0.358�@�s���Y�ƁC���i����0.439�@�d�C�E�K�X�E�M�����E������0.230
���Ȃ݂ɓޗnj��̈�t�݂̘b�ŋȐ���`���Ɓi�s�����P�ʁj
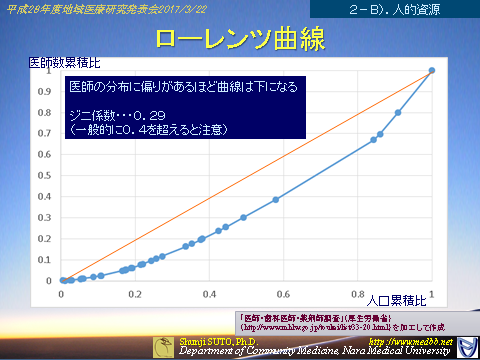
�i�f�[�^���͂���l����n���Ẩۑ��@���j
�����Ƃ��n��ʈ�t���݂̘b�������������ׂĂ����������킯�ł��Ȃ��ł����A�͈͂����߂Ă����قǕ݂͐�����킯�ł�����E�E�E
���\�[�X�̒n���I�ȕ���[���ɂ��邱�Ƃ��̂��͖̂ړI�ł͂Ȃ������ɋ߂Â���i�ł����āA�ɂȂ�ׂ��肪�łȂ��悤�Ȕz�����ł���d�g�݂Ƃ̃p�b�P�[�W�ƍl���Ă���܂�
�x�����z�\����ɂ������ϒl�̌v�Z�@�ɂ��āi�Čf�j
���i�K���l�~�x���j�^�ϑ���
�����l
median�i�ʖ���Q�l���ʐ��j�ʓI�ϗʂ������ړx�ŏ���������\�l
���Ԃɕ��ׂ��Ƃ��^�̏��ʂɂ����̂̒l
�̐��������̎��͐^��2�̐��l�̕��ϒl
�X�L�[�W�����v�̔�^�_�͒����l�I�ȃm���ŎZ�p���ς��Ă���
�X�L�[�W�����v��m�낤�I�I���[������i�W�����v��O�~���N�j
https://www.meg-snow.com/jump/rule/rule.html
�ŕp�l
mode�i���s�C�͂��j�Ⴄ�Ӗ��Ő��̗��_�i�������j�̐��E
�ʓI�ϗʂ𖼋`�ړx�ŏ���������\�l
���`�ړx�ł킩�邱�Ƃ͈ꏏ���Ⴄ��
�K�����ɓx�����J�E���g
��ԑ����Ƃ���̊K���l
��ʂ����_�̎��͕��L�i���ς��Ƃ�Ɓ@�����I���D���I�H��ԂɂȂ�j
�U�z�x
dispersion�ő�l�ƍŏ��l���g��
�ő�l�ƍŏ��l���킩����̏W�c�̃o���c�L���킩���ő�lmaximum excel max��
�ŏ��lminimum excel min��
�͈�
RangeR=�ő�l�|�ŏ��l
����
�@�O��l���Ђ炤
�@�Z�o���p��
�l���ʐ����g��
Quartile���������i�����j�ɕ��ׂďW�c��4����
��P�l���ʐ� First Quartile:Q1 =�@25th percentile 25%�^�C���l
��Q�l���ʐ� Second Quartile:Q2 = 50th percentile 50%�^�C���l�@���@Median�@�����l
��R�l���ʐ� Third Quartile:Q3 =�@75th percentile 75%�^�C���l
�l���ʐ��̋��ߕ��E�E�E�����ɂ͐���ނ���(P41)
���̎��Ƃ̐��E�ł̎�茈��
�l���ʂ͓��Ɏw�肵�Ȃ�����tukey�̃q���W��
http://medbb.exblog.jp/12047409/
�l���ʔ͈�
IQR(interquartile range)IQR=Q3-Q1
�l���ʕ�
QD(Quartile Deviation)QD=IQR/2
�͈͂͏W�c���O���猩���o���c�L���C���[�W
���͏W�c�̓����̂���l����̃o���c�L���C���[�W
���ϒl���g��
mean��
Deviation���Ƃ��Ƃ͕W���ƂȂ鐔�l����̃Y���i��j���Ӗ�������̂������v�̐��E�ł͏W�c�̕��ϒl����̃Y��������
���̕��ς��Ƃ�ΏW�c���̊e�X�̃Y�����Ղ肪�킩��@���@���v�͏�ɂO�@�̂ɕ��ς���ɂO
���U
varianceV�@excel����VAR
�����悵�����̂̕���
�W����
Standard Deviation�L���͕W�{�W����s�@��W������
s=��V
�i�̂�V��s^2���^2�ŕ\������j
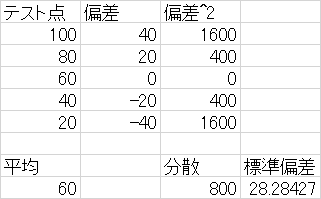
���B�x�m�F
�P�j�x�����z�\��A,B,C�ɓ��鐔�l�����߂��Q�j�x�����z�\���畽�ϒl�����߂�
�R�j�Ȃ��A�ꕪ�U�̒��悢����ł���s�Ε��U�ł͕������a��n�ł͂Ȃ�n-1�Ŋ���̂�
| �K�� | �K���l | �x�� | ���Γx�� | �ݐϓx�� | �ݐϑ��Γx�� |
|---|---|---|---|---|---|
| 0.5�`1.0 | |||||
| 1.0�`1.5 | 6 | A | 0.325 | ||
| 1.5�`2.0 | 0.1 | 17 | |||
| 2.0�`2.5 | B | 0.65 | |||
| 2.5�`3.0 | 7 | ||||
| 3.0�`3.5 | 0.125 | C | |||
| 3.5�`4.0 | |||||
| �v | ----- | 1.00 | ----- | ----- |
�⑫
|
�{���̗]�k �L�����p�X�ړ]�ɔ���������傪�u�������v ����҃W�����{�i�ǔ��e���r�j http://www.ytv.co.jp/machiisha/ �h�����l��������h���̈ꌾ�̂��߂Ɂi�v���t�F�b�V���i���d���̗��V�@NHK�j http://www.nhk.or.jp/professional/2009/0113/ ���ȏ��Y���y�[�W ��2�́iP21-27,P41�j ���[�����c�Ȑ��̘b�����i���𑪂�w�W �|�W�j�W���ƃ��[�����c�Ȑ��|�i�Ƃ�܌o�ό���2005�N4���jhttp://www.pref.toyama.jp/sections/1015/ecm/back/2005apr/shihyo/ ���U�̂Ƃ��낿����Ɛ������Ă����܂��傤�B ���ȏ��ł͕W�{�W������s�Ε��U�ɂ����̂Ƃ��Ă���̂� �i���p�セ��ł悢���A�������Ȃ��悤�ɐ����j �ꕪ�U ��^2�F��W�c�̕��U�E�E�E�S�v�f�̒l���K�v �W�{���U ��^2�F�W�{�̕��U�E�E�E�W�{�̒l���K�v �s�Ε��U ��^2�F�W�{���ꕪ�U�̕s�ΐ���ʂ����Ƃ߂����� ���Q�l���W�{����, �W�{���U, �s�Ε��U�i������w�H�w���d�C�d�q�H�w�ȓd�q�V�X�e���H�w�u��(�y����)���� ���j http://dsl4.eee.u-ryukyu.ac.jp/DOCS/error/node19.html �W�{���U�ƕs�Ε��U���ǂ�����ꕪ�U�̐���l�E���ϒl�̐���Ƃ̓��P���Ⴄ ��L�T�C�g������p�u���K���z�ɑ�, �W�{���ς͕��ς̍Ŗސ���ʂ��s�ΐ���ʂȂ̂ł��邪, �W�{���U�͕��U�̍Ŗސ���ʂł͂��邪�s�ΐ���ʂł͂Ȃ�, �s�Ε��U�͕��U�̕s�ΐ���ʂł͂��邪�Ŗސ���ʂł͂Ȃ��B �v ���B�x�m�F�̂��ꂱ���P�j�[�f�[�^�͑��݂��܂����Q�j�����[�f�[�^�����݂��Ă�����Ōv�Z�����Ȃ�Γ����悤�Ȓl���o�Ă��܂��i���R�ł����j �R�j���ȏ�P23�Q�ƁB�W�{�̕��ςƂ̕��̘a�͕K���[���ł����A�ꕽ�ρi���W�{���ς̏ꍇ�j�Ƃ̕��̘a�̓[���ɂȂ�Ȃ��@�Ƃ������Ƃ��C���[�W���Ă���Α��v�ł��傤 |
��4��@���ϒl�̐���
���B�ڕW�S�|�P�W�����ƕW���덷�̈Ⴂ������ł���
�S�|�Q�ꕪ�U�����m�̏ꍇ�ł��ꕽ�ς���Ԑ���ł���
����
��W�c���璊�o�����W�{����ɕ�W�c�̕��z�������l�i�ꐔ�j�𐄑������_����Ƌ�Ԑ��肪����
�_����
��̒l�Ő����ꕽ�ς̐���l�͕W�{����
�ꕪ�U�̐���l�͕s�Ε��U
��Ԑ���
�ꐔ������m���œ��镝������������l�{���̖ڕW��P70�̘b�𗝉����邱�ƁB�ꕽ�ς͈��Ȃ̂ɕW�{���ς͕W�{���ɈقȂ�̂ŕ�����������
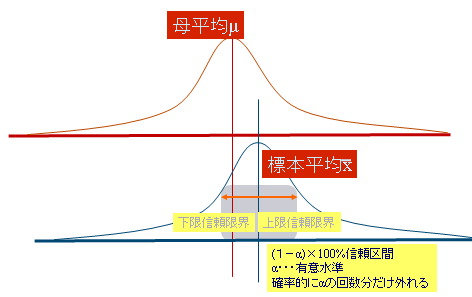
�W�{���ςɕ����������邱�ƂŁA���̘g���ɕꕽ�ς�����B�����ϒl�̃o��������W���덷�@SE=��/��n
���K���z
���E�Ώ̂̒ޏ��z�i���ȏ�P32-40�j���ϒl�ɋ߂��قǏo������������������ɏ]���ĒႭ�Ȃ�i���Ƃ������j
�������m�������ŌJ��Ԃ��Ɛ��K���z�Ƃ����b
�|�C���g�́u�َ��ȏW�c�̌v���l���g�ݍ��킳�������z�͐��K���z�ƂȂ�Ȃ��v�i���ȏ�P33�j�n�Y�Ȃ̂ł����E�E�E
������b�����錟��̘b�͂��̕������L�[�ƂȂ�܂����A�َ��ȏW�c���ꏏ�Ɣ��肵����A�ꏏ�ȏW�c���َ��Ɣ��肵����B���������َ����āH�������āH
���K���z���ۂ��`��̔��f��P28�@�c�x�@��x���Q��
���ȏ��ɂ͌���\�����Ă���܂����i�܂����ƂŌ���̘b�͈���Ă���܂���̂Łj�E�E�E������̋@���
���肷��Ƃ��ɂ́u���z�̐��K���v�Ɋւ��ăf�[�^�����傫����ΐ���Ȃ��Ȃ̂ŁiP6�j�A����܂�E�E�E
�^�x�Ɛ��x�̘b�i�덷�j�ɒu�������

��i�����K���z�B���L���肪�E�ɍs���قǍL����
���̒i�͗ǂ��킩��Ȃ����z�ɂȂ邪�A�Ⴆ��P35�̂悤�ȍ������z�̏ꍇ�����肤��
���@�M����Ԍ��E�w���E�E�E�W�����K���z��z�X�R�A�̂���
�W�����K���z
���ϒl���O�W�������P�i���U���P�j�ɂȂ�悤�ɒl��ϊ���������
���l�͕��ϒl��50�A�W�������P�O�ɂȂ�悤�ɒl��ϊ���������
���S�Ɍ��藝
�W�{�̑傫�����\���ł���ΕW�{���ς̕��z�͐��K���z�@�����������肳��Ă���̂ł�����R�덷�̔����͐��K���z�ɏ]��
�@������𑝂₹�Α��₷�ق�
�W�����ƕW���덷
�i���ȏ�P52�j�E�W�����͕W�{�̕��z�̃o���c�L�������������
�E�W���덷�͕�W�c���璊�o�����W�{�̕��ϒl�̃o���c�L�
SE=�Ё^��n
�덷�`���̖@���̘b�ōl����Ɨǂ�
�����ߋ��ɗ��R����������Ƃ��̎���
http://www.medbb.net/education/ocrstat2015/index.html
��W���������m�̏ꍇ�̋�Ԑ���
�i���ȏ�P70�j���K���z�\�łȂ�1.96�ɂȂ�̂��m�F
��W���������m�̏ꍇ�̋�Ԑ���
�i���ȏ�P70�j���K���z�͕ꕽ�ϒl�ƕ�W������������Ȃ��Ǝg���Ȃ���n�������ꍇ�W�{���ςƕW�{�W�����ŋߎ��ł��邪
n�����Ȃ��ꍇ�͋ߎ��ł��Ȃ���t���z(�W�{�̎��R�x�˂����킩���Ă���A��͌��蓝�v�ʂ����߂�Ίm�����킩��)
�����z
P64-66
���R�x�݂̂ł��܂�m�����z
���R�x�E�E�E�W�{�̒��Ŏ��R�ɐU�镑�����Ƃ�������Ă���̂̐�
�@�@�@�@�@�@���v�l���ꐔ�̐���ƂȂ�ƁA���R�ɐU�镑���Ȃ��̂��o�Ă���i���܍��킹�j
�W�{���U�͕����a���̂̐��ŏ����邱�Ƃŋ��߂邪�ꕪ�U�̂قǂ悢����ł���s�Ε��U��n-1�i���R�x�j�ŏ�����
���B�x�m�F
�P�jP11���G�Ȓ����f�[�^��TG��95%�M����Ԃ����߂��Q�jP39���̃P�[�X��88�_�̏ꍇ�A���l�Ə�ʂ��牽�ԖڂɂȂ邩���߂�
�R�j�W�{�W�������ς�炸�T���v������5�{�ɂȂ������A�W���덷�͂ǂ̒��x�ω�����̂��H
�⑫
���ȏ��Y���y�[�W��2�́iP28,32-37�j��3�́iP52-53�j ��4�́iP64-66,70-71�j �{���̗]�k���ۍ~���Ă��Ȃ��J�\���A�C�ے� �R�A�����[�_�[���(47NEWS)https://this.kiji.is/231273048212111364?c=39546741839462401 �Ȋw�̘b�Ƃ������ƂŁA���؉\���̂��Ƃ��A���ԂƂ̘����̘b��� �{���͊w���ɂ��Ă݂�Ε��i�̌��j���A�Љ�l�ɂƂ��Ă͔������x�݂Ƃ��������ł���
����tweet�ɑN�����o�ꂵ���Ƃ��͐S���₩�ő��₩�ɋA��Ă���T�C���ł�����܂� http://twilog.org/medbb/search?word=%E9%AE%AE%E9%AD%9A&ao=a ����youtube����ň�Ԑl�C������̂�����B �o�_���Z�Z�́i�Ă̍b�q����98����i���o��j�ɂāj2016�N8��7�� ���B�x�m�F���ꂱ���P�j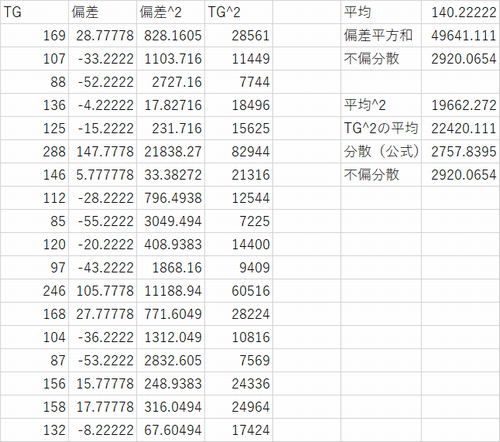 ���U�͓��̕��ρ|���ς̓��ŋ��߂��܂����s�Ε��U�����߂�̂�n/n-1�{���Ă��������B ����͑S�����������킯�ł͂Ȃ��̂Łi�O�̂��߁j �ꕪ�U�͕s���Ȃ̂ŐM����Ԍ��E�W����t���z�\��� ��Ԑ���̏ꍇ��������͋�ԂɊ܂ނ��ۂ��̘b������܂������A�����g���Ă��邯�[���������ł��i�m�����j�B ���ȏ��̐��K���z�\�ł͗����m����������Ă��܂������l�̓_���܂ޖʐς�������Ă��܂� �ƂȂ�Ɓ����g���ق����ƌ��������Ȃ�܂����A�Ⴄ���z�\�i�Ⴆ�ΐf�Ï��Ǘ��m�̂��߂̂₳�������v�w�i���ق��j�j������� ���S�������܂ł̖ʐς�������Ă��܂���Z=1.96�̎���0.4750�ƂȂ��Ă��܂��B �i�܂����Ƃ����Ă��܂��j����̏ꍇ�m�����L�Ӑ����������ۂ��Ŕ��f���܂��̂ŁA������Ɛ����������Ƌ�Ԑ���́��ŗǂ����� �Q�jZ=(88-55)/15=2.2 �W�����K���z�\��藼����0.02780 �㑤�����Ȃ̂�0.0139�~400�l=5.56�l�Ƃ������Ƃ�6�l���x�Ɛ�������� �R�j1/��5��0.447�{�Ɍ������� �����d��̌������̎��ɂ��܂�n�C�X�y�b�N�Ȃ��̂��������܂��Ɓi�v���O���}�u���d��Ƃ��j��₱�������ƂɂȂ�̂ł��̎|�����O�ɂ͋�����������Ǝv���܂� �l�����Z���o���ĕ����������߂�����̂ł��̎����͏���܂��B���l�̌�����̘b�ǂ��ɂł����̉�]�������l�Ԃ͑��݂���Ƃ����b����@�Ƒ̗́i���C�j�̂Ƃ��낪�Ⴂ�ƂȂ��Ă���Ǝv���Ă��܂��B ����͕₦��\���������킯�ŁE�E�E�Ƃ����b |
��5��@�L�q���v�i�W�j�|���W���E��A����
���B�ڕW�T�|�P���W��������E�v�Z���邱�Ƃ��o����
�T�|�Q��A�������ǂ̂悤�Ȃ��̂��������邱�Ƃ��o����
����
�i���ȏ�P174�j correlative���֊W������E�E�E�֘A������
���֊W�������E�E�E�֘A���Ȃ�
�����̉e�����邩�Ȃ���
����
cause and effect�����ƌ���
���ʊW������E�E�E�e��������
���ʊW�������E�E�E�e�����Ȃ�
���ʂ͊֘A������i���ւ�����j���e�����y�ڂ��W�i���ʊW������j�ƍl����i�l�������Ȃ�j
��
�������z���|�x����E�E�E�E���֊W��
�^�o�R���z���l�ɃR�[�q�[�����ސl�������̂́E�E�E�iyahoo�m�b�܁j
http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1293675642
���̊W���g����
�R�[�q�[�����ށ|�x����E�E�E���֊W��
�ł��R�[�q�[���x����̌����Ƃ͂�����Ȃ�
�R�[�q�[�����҂ɔx���������R�́H�����K���Ƃ̊֘A������
�A�����J�Ŗ�50���l��Ώۂɂ�����������
from International journal of epidemiology
http://medley.life/news/item/5589521b660815fe00d5ec8e
�R�[�q�[�Ɣx����̑��֊W�Ɋ��荞��ł���i�ǂ���Ƃ����֊W������j��ԁ���)
���荞��ł��邻�ꁁ�𗍈��q�E�E�E����
�R�[�q�[�Ɣx����Ɉ��ʊW�������Ƃ����Ȃ炻�̊W�͋^������
��F�d�Ԃɏ��Ƃ��F�����ꂼ��w�Ɍ������Ē��ǂ������Ă�悤�Ɍ����邪�A�݂��ɊW�͖����B
�{���Ɓi���v�w�j�͈�Ìn�ΏۂŁu�����Â��y�ڂ��e���₻�̗v���Ɋւ���@�����������������@��T������w�╪��v
�i��ナ�n�r���e�[�V�������w�Z�@���v�w�Q�O�P�T�i���w�Ö@�w�ȁj���j
�m�肽���̂́u�e���v�ł��邩��ړI��������Ȃ��悤��
���}
X����Y���Ɉ�̑Ώۂɗ^�����邻�ꂼ��̒l���v���b�g�i��F�g���Ƒ̏d�j�Ƃ肠�����}�ɂ���ƊW�������I�ɂ킩��i�ꍇ�����遨�𗍌��ی��ݍ�p�ɒ��Ӂj
���W��
-1����1�܂ł̒l���Ƃ�i���ȏ�P174�j�{�̏ꍇ���̑��ց@�|�̏ꍇ���̑���
X�����������Y����������E�E�E1
X�����������Y�͌�������E�E�E-1
X���������悤���������悤��Y�͊W�Ȃ��E�E�E0
���W����0�o�Ȃ���Α��ւ́u����v���P�������x�͐�����0���痣���قNj����Ȃ�
��ʂɁ`0.2�ł���Α��ւ͂Ȃ��A0.7�`�ł���������ւ̖ڈ��Ƃ���Ă�B
X���Ō����Ƃ��̃o���c�L���Y���Ō����Ƃ��̃o���c�L������Ɍv�Z���Ă�
�o���c�L���U�z�x�E�E�E���U�E�E�E���̓��̕���
�����U������Ώۂ�X���̕���Y���̕����悶�����̂��x�[�X
����
��{�����̂Ƃ���͕������a�̘b�ɂȂ��Ă��邪�W�{���U�̏ꍇ���ӂ�n�Ŋ���Ȃ��Ƃ����Ȃ�
����ƁE�E�E���̕��ρ|���ς̓��@�Ƃ������Y�����̂���������o����
�@�@
| X�̕� | Y�̕� | �悶������ |
|---|---|---|
| �{ | �{ | �{ |
| �{ | �| | �| |
| �| | �{ | �| |
| �| | �| | �{ |
�����U��X��Y���̃o���c�L����������Ă���̂ł��̂܂܂̐������Ɖ��߂��ɂ�����X��Y�̕W�����ŏ�����i���K���j�����W��
�����Ŗ����ꍇ�͕ϊ��i�Ⴆ�Αΐ��ϊ��j���Ă���v�Z���Ă��悢�i�ΐ��O���t�j
�ΐ��O���t�̗�i���ᎆ�l�b�g�j
http://houganshi.net/taisuu.php
��A����
X���̒l��Y���̒l�𐔎��iy=ax+b�j�Ŏ����������������Ƃ��ɂ��ꂼ��̓_����̍��i�c���j��2�悵�đ��������́i�����a�j���ł����������̐�������A����
����W��
���W�����悷��Ƌ��߂��������ɂ���Đ����ł��銄���������B�i��^���Ƃ��j
�܂荂��������قǐ����Ő����o���邱�ƂɂȂ�
�f���y�[�W�iP182���35�j�⑫
�ϐ��̒�`�Ɨ��ϐ��E�E�Einput�i�R���g���[���o����j
�]���ϐ��E�E�Eoutput�i�n�ɂ���Č��܂�j
���B�x�m�F
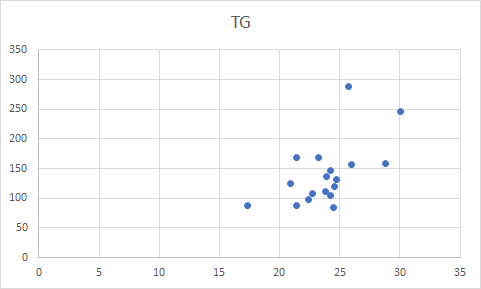
�P�jP11���G�Ȓ����f�[�^��BMI��TG�̑��W�������߂��Q�j�P�j�̉�A��������ь���W���A��A�����̎���̕W���������߂�
�⑫
�{���̗]�k�l�������^�����Љ�ɂ���
�e�j�X�ɍs���\�肪����̂ɁA�A���R�[���őz�肵�Ă������Ԃ��I�[�o�[�E�E�E �^�N�V�[���^�悭���܂�^�]��Ƙb�����Ȃ���E�E�E 15������R���T�[�g�����Ă������ƁA�N�̃R���T�[�g���A�z��I�����Ԃ������Ă��ꂽ�i�������̗\�z�{1���ԁj �^�]�肳��������Ƃɕt�߂��E���E�����Ă����͗l�B�������ۋ�`�ɍs���l��get�ł����� �c�O�Ȃ��玄�����͈�������A����ł��A���R�[���r���Ŕ����o���l�͋}���ł���킯�ł�����B 50cc�o�C�N�̌� 50�t�o�C�N���j�[�Y�̌����Ɣr�K�X�K���� �ڑO�ɔ�����50cc�o�C�N�̖ŖS�iITmedia �r�W�l�X�I�����C���j http://www.itmedia.co.jp/business/articles/1705/08/news040.html �d�����̘b�B��������ς��Ȃ��炻�̊��i���߂��Ă�����́j�ɂ��������̂���Ȃ��Ă͂Ȃ�Ȃ� �i�]�k�j50cc�̐������x��30km/h�ł��B�C�����ĉ^�]���܂��傤 �i�]�k�j���]�Ԃ������܂肪�������Ȃ��Ă��܂��B�݂Ȃ��]�Ԃł����S�^�]�� �P�K�ɂ͋C�����܂��傤�̘b ���̌�̃e�j�X�ɂāE�E�E�B �Ⴂ�����͑��v�ł����N��ƂƂ��ɓ��O�ȏ������i�^���_�o�̗D��Ă�����قǓ��̓I�Ȃ��̂Ɗ��o����������ł��낤�j ���ȏ��Y���y�[�W��1�́iP17�j��9�́iP174-179,195-202�j ���ƕ⑫�L�Ӎ��̘b�́A��8��@����̌����Ő�������\��ł��̂ŁA����̂Ƃ���̓X���[���܂� �i���ȏ�P180r�\�̘b�Ȃǂ͂��̎��Ɂj ���B�x�m�F���ꂱ�����ȏ�P198���K19���߂������i��P261�j |
��6��@���x�E���ٓx�EROC�Ȑ�
���B�ڕW�U�|�P���ʓ����l�̌v�Z���o����
�U�|�Q�]�����ʂ��ROC�Ȑ����쐬���]����J�b�g�I�t�l�̌������o����
�����@�̐f�f�I�L�p����]������b
�L�a���̉e������w�W�A�Ȃ��w�W�����Ă�������
|
�u���v�ł͂��邪���ۂɂ͊����B���_�L�a���Ƃ������i���ԗL�a���͎��_�L�a���Ɋ��Ԓ��̜늳�����������́j ��Ɨ��Ɗ����̈Ⴂ�ɂ��� ��E�E�E�قȂ���̂��r�i���P�ʂɂȂ�ꍇ�����邪�j ���E�E�E�䂾�����ԂƔ�r�i�P�ʂ�/sec�@/min�@/hr�@�ƂȂ�j �����E�E�S�̂ƈꕔ�i�������́j���r�i���P�ʁj �ȉ��Q�l�ɂ��Ă������� ��13��@��Ó��v�i�U�j�|��Ɨ��Ɗ����i���ی���Ñ�w�@��Ï��w�Q�O�P�U�j http://www.medbb.net/education/ohsumedinfo2016/#13 |
���x�Ɠ��ٓx
���ȏ��iP116�j���x��P(�z��|�c) �@�����Q�ɂ�����^�z���̊���
�U�z������P(�z��|�cc) ���Q�ɂ�����U�z���̊���
���ٓx���P�|�U�z���� ���Q�ɂ�����^�A���̊���
�\���l
�L�a���̉e������
�@�z���I������P(�c|�z��)
�@�A���I������P(�cc|�A��)
�����@�̕]���w�W
�@�ޓx�䁁���x/�U�z�����@
�@�I�b�Y�䁁���ȏ��Q�Ɓ@�����̗L�p��
�@ROC�|AUC��ROC�Ȑ���`���ĎZ�o�@�����̕��ʔ\
���ł��z���Ɣ��f���錟���͊��x���U�z�������P�ɂȂ�
�i�Ȃ�ł�����ł��A����܂�!�I�@�̃m���j
ROC�Ȑ�
���ȏ��iP119�j���ʓx�̕���
���x�ƋU�z�����i�P�|���ٓx�j��p���ċȐ���`��
���21�ŇE���J�b�g�I�t�l�Ƃ����Ƃ��̗z���I������7/9�@�A���I����=8/11
���B�x�m�F
�P�j�Ȃ��\���l�i�Ⴆ�Ηz���I�����j�͗L�a���̉e�����A���x�͉e�����Ȃ����Ȍ��ɏq�ׂ��Q�j���̃}�����O���t�B�̌������ʂ���ROC�Ȑ���`���AAUC���i�����_�ȉ�2���܂ŋ��ߎl�̌ܓ��j���߂�
���Q�l��
�X�{ �����C���{�̓������f�̗��j�Ɖۑ�C���������f�w��C18(3)211-231,2009
https://www.jstage.jst.go.jp/article/jjabcs/18/3/18_3_211/_article/references/-char/ja/
�R�jP124��CK�̃J�b�g�I�t�l�����ꂼ��
���Q�l��
�w���p���ʊ�͈́i���{�Տ�������w��ݒ�A2011�j�i���{�Տ�������w��j
http://www.jslm.org/committees/standard/ref_2011.html
| �ُ�Ȃ��i�P�j | �ǐ��i�Q�j | ������ے�ł��Ȃ��i�R�j | �����̋^���i�S�j | �����i�T�j | �v | |
|---|---|---|---|---|---|---|
| �����Q | 0 | 4 | 14 | 12 | 10 | 40 |
| ���Q | 20 | 20 | 12 | 8 | 0 | 60 |
�⑫
�{���̗]�k�̑O�̗]�k��̓��̘b����͑��s���i�V�Z�j�Ɋ���Ă���E�E�E �`�����E�b�h2017 http://www.mbs.jp/challywood/index.shtml http://www.mbs.jp/challywood/event/ �T�C�G���X�V���[�i�{���g�{���Y ���ă^���ɂȂ�I�T�C�G���X�V���[�j���݂܂����B SNS�ɓ���̓_���Ƃ���������Ă����̂ŐÎ~��ňꖇ�����グ�܂����B �q�ǂ������͑��тł���
��C�C�̌����i�@���ۊO�������ރ��C�u�����[�@���F���c�@�l ���ԕ������狦��j http://www.tokiwa.ac.jp/~kudou/experiment/s3003.php �w���ՂȂǂŊF�������ʂ̕��X�ɋ����������Ă݂Ă���������悤�ȍH�v���B �ǂ̂悤�ȃO�b�Y��z���Ă��邩���Q�l�ɂȂ�Ǝv���܂� �{���̗]�k�A�j�T�L�X�ɂ��H���ł�\�h���܂��傤�i�����J���ȁjhttp://www.mhlw.go.jp/stf/seisakunitsuite/bunya/0000042953.html �H���œ��v�����i�����J���ȁj http://www.mhlw.go.jp/toukei/list/112-1.html �H���œ��v�쐬�v�� http://www.mhlw.go.jp/stf/shingi/2r9852000002xk88-att/2r9852000002xkjo.pdf �A�j�T�L�X�H���ł��}���A�n�Ӓ����u���ɂ����ċ������v �Ώ��@�́H�iThe Huffington Post Japan�j http://www.huffingtonpost.jp/2017/05/13/anisakis_n_16599196.html �ȉ��L�������p �u��Ë@�ւɐϋɓI�ȕ����߂Ĉȍ~�A�͑����X���v �u����Ȃ��P�[�X�������A���҂͐��v�ŔN��7000�l�ȏ�ɂȂ�Ƃ݂��Ă���v �u����ނ̗��ʎ���ω����A�Ⓚ�łȂ����̏�ԂŎ�������P�[�X�����������Ƃ���Q�����̗v���Ɛ���v ���v�f�[�^�̐M�����̘b�ƁA�Љ�̊��ω��̘b�� ���ȏ��Y���y�[�W��6�́iP116-124�j���B�x�m�F���ꂱ���P�j�L�a�����オ���a��c��b��d���Q�jAUC=0.85 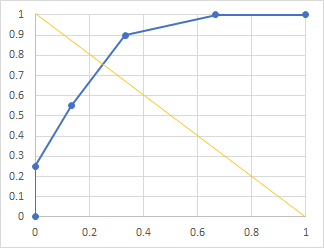 �R�j �@a�@�^�z���@�Q�V �@b�@�U�z���@�@�U �@c�@�U�A���@�@�R �@d�@�^�A���@�P�S �@���x�@�@�@�Q�V�^�R�O���O�D�X �@���ٓx�@�@�P�S�^�Q�O���O�D�V �@�ޓx��@�@�O�D�X�^�O�D�R���R �@�I�b�Y��@�i�Q�V�^�R�j�^�i�U�^�P�S�j���Q�P |
��7��@���Ί댯�x
���B�ڕW�V�|�P���Ί댯�x�������w�W�ɂǂ̂悤�Ȃ��̂����邩�����ł���@
�V�|�Q�Ǘ�Ώƌ����ł͑��Ί댯���I�b�Y��ŎZ�o���闝�R������ł���
���ւ��֘A���ǂ̒��x���邩
���f���͂́A�������ʂ���ɂǂ̂悤�����f���Ă����̂��i�������ʂƎ����̘b�j
���Ί댯�x�̘b�́A�����i���ʁj�����I�i�����j���e�����ǂ̒��x�Ă���̂�
�w�W�͐����Ƃ��Čv�Z�o������茋�ʂ������̂����A����̉��߂����Ȃ��悤�ɂ��邱�Ƃł�������A�����������߂��悤�������̂ŏo���Ă��Ӗ��Ȃ��̏ꍇ������
���̎��Ƃł͑��Ί댯�x=Relative Risk �͈�ʓI�ȗp��ł���A���̎Z�o�w�W�̈�ɑ��Ί댯�����X�N��iRisk Ratio�j������Ɛ������܂�
��ʓI�ɂ͂�����ւ�̌��t�S�`���S�`���ł��B
������@�̘b
���ȏ�P220�Q�ƁE�E�E�ώ@�����ł͌Q�Ԕ�r�ɗL�Ӎ����g���Ȃ��H���ԁi����j�𖾂炩�ɂ����Ƃ���ŁA���̎�����P���Ɋg���ł���킯�ł͂Ȃ��B
���ԂɊ�Â��b�͎��������������̂́A��������߂Ɍ������Ă��܂������W�J���ł��Ȃ��Ȃ�����B
�ώ@����(Observational study)
���f�����iCross-sectional study�j���I�Ǝ������ɕ]��
���Ԏ����Ȃ��ꍇ�������i��O�͐��ʂȂǁj���ʊW�܂ł͕s���ɂȂ��Ă��܂��₷��
�R�z�[�g�����iCohort study�j
�Ώۂɔ��I���Ă���l�X��c�����A���̒����甘�I�Q�ƔI�Q��ݒ�A�ǐՒ������Ă����X�^�C��
�ʏ�O���������A�������ɂ݂��ړI�R�z�[�g�����Ƃ����̂�����B�i��X�ł����I�Q�Ɋւ�������ꍇ�j
�Ǘ�Ώƌ����iCase-control study�j
�����ԁi�Ⴆ�Εa�C�ɜ늳���Ă���j�Q�ƁA�늳���Ă��Ȃ��Q��ݒ�A���Ԃ�k���Ē������Ă����X�^�C��
�������ɂ����s���Ȃ��i�O�������Ɣ��I�������̏������������Ȃ�j
�����I�����i��������j�iintervention study�j
�R�z�[�g�����̏ꍇ�A���I�Q�i����Q�j�������҂�����t����@���@�팱�҂ɑ���ϗ��I�z�����̗v����ׂɊ���t���邱�Ƃ��o����ꍇ�͌𗍈��q�𐧌�ł���i���Ƃ����҂����j
�ϗ��I�ɍl����Ɣ����Q�̕����s���v�ɂȂ��Ă��܂��\���������̂ŁA�z�����������f�U�C�������߂���
�����p�f�[�^
| ���a���� | ���a�� | �v | |
|---|---|---|---|
| ���I�L | A | B | A+B |
| ���I�� | C | D | C+D |
| �v | A+C | B+D |
���Ί댯
Risk Ratio(RR)�u���X�N��v�ƌ����������킩��悢�i�Ǝv�����j
���I�i����j�̗L�鎞�Ɩ��̎��̊댯�������w�W�̔�
�댯�������w�W�ɂ͜늳�����L�a����玀�S�����
A�`D:���a�����p�x�i�p�x�ȊO�ɜ늳�����L�a���E�E�E�j
���I�L�Q�̔��ǃ��X�N��A/(A+B)
���I���Q�̔��ǃ��X�N��C/(C+D)
���X�N�䁁A/(A+B)�^C/(C+D)
�����A�����p�x���Ⴏ���A+B��B�@C+D��D
�@���X�N���A/B�^C/D��AD/BC
�I�b�Y��
Odds Ratio(OR)�u���X�N��v���o���Ȃ��ꍇ�ł��o����i���X�N��͂��ꂼ��̌Q�̃��X�N���킩���Ă��Ȃ��Əo���Ȃ��j
�댯�Ȏ��ۂ��N�����ꍇ�ƋN���Ȃ������ꍇ�x���̔�i���I�b�Y�j�ɂ��Ĕ��I�i����j�̗L�����ɋ��ߔ���Ƃ�������
���ǗL�Q�̔��I�I�b�Y��A/C
���ǖ��Q�̔��I�I�b�Y��B/D
�I�b�Y�䁁A/C�^B/D
�@�@�@�@��AD/BC
��L�̂悤�ɔ��Ǖp�x���Ⴏ��I�b�Y��ƃ��X�N��̋ߎ��l�ƂȂ�
���B�x�m�F
�R�z�[�g�ƏǗ�Ώƌ��������ōs���Ă������̂Ƃ���B�P�j���ꂼ�ꂩ�瑊�Ί댯�x�i���X�N��������̓I�b�Y��j�����߂�
�Q�j���X�N��ƃI�b�Y�䂪�ߎ��l�ƂȂ�������q�ׂ�
�R�j�Ǘ�Ώƌ����ł͂Ȃ����X�N������߂Ă����Ί댯�x�Ƃ��Ă̎w�W�Ƃ��ēK�ł͂Ȃ��̂��B�Ȍ��ɏq�ׂ�
�S�j��������ł͗ϗ��I�Ȗ��ɒ��ӂ��Ȃ��Ă͂Ȃ�Ȃ����i�[���H�����̍l�����Ȍ��ɏq�ׂ�
�T�j�o�P�P�O���P�X�̃f�[�^��p���Ċ�͈͂�M:10�`50�@F:10�`30�@�Ƃ������̑��Ί댯�x�����߂�
���Q�l��
�w���p���ʊ�͈́i���{�Տ�������w��ݒ�A2011�j�i���{�Տ�������w��j
http://www.jslm.org/committees/standard/ref_2011.html
�R�z�[�g����
| �s�������� | �s�����Ȃ� | �v | |
|---|---|---|---|
| ���I�Q | 100 | 1900 | 2000 |
| �I�Q | 50 | 1950 | 2000 |
| �v | 150 | 3850 | 4000 |
| �s�������� | �s�������� | �v | |
|---|---|---|---|
| ���I������ | 50 | 30 | 80 |
| ���I�� | 50 | 70 | 120 |
| �v | 100 | 100 |
�⑫
�����̗]�k���̒��͋����b�L���Ɓi�v���j�Ƃ���ɏo�邱�Ƃŋ�����m�遨�U���̊u����
�{�w�ɂ���F����̃����b�g�̈�Ƃ��āA��w��ÂɊւ���Ƃ���ł��̋��������̌��ł���Ƃ��� �Ȃ̂Ōq���邱�Ƃɒ��͂���̂ł͂Ȃ��A�q���������Ɏ��g�̔\�͂��\�������ł���悤���X�߂����Ă��������B ���Ȃ݂ɁA�O�ɍ����Ă����搶�Ƃ͊w�����ォ�瑶���グ�Ă��邪�A�ɂ��Ȃ���̐搶 ���̎w�������̃{�X����̌q����Ǝv���Ă����̂ł����i������Ԉ���Ă��Ȃ��̂ł����j�w�������Ƃ͈قȂ鉶�t�̐搶�̒�搶����̃��C���Ɛ��������������m�Ȃ悤�ŁB �v���O�����b�N�̃o���h�����o�[�̕ϑJ���v�������ׂĂ��܂��� ���Q�l�����q�J�[�����O�̃v���O���b�V�u�E���b�N�Ȑ��E�i�X�~���m�t���������E�F�b�u���O���{��Łj http://sueme.jugem.jp/?eid=1598 ���Ȃ݂ɂł����A�����l���ی�@�Ɋւ��ċ����̂�����͘A�����������B ���B�x�m�F���ꂱ���P�j�i�R�z�[�g�j�����X�N��@�i100/2000�j�^�i50/2000�j���Q�D�O�@�@�i�Ǘ�Ώی����j�I�b�Y��@�i50/50�j�^�i30/70�j���Q�D�R ���Ȃ݂� �@�i�R�z�[�g�j�I�b�Y��@�i100/50�j�^�i1900/1950�j���Q�D�O�T �@�i�Ǘ�Ώی����j�����X�N��@�i50/80�j�^�i50/120�j���P�D�T �Q�j�� �R�j�� �S�j�� �T�j�댯���i�����j�����悢����ƌ����邩�ۂ� ����̑ΏۏW�c�͖\�I�Q�i�j���j��\�I�Q�i�����j�ƍl����Ƃ�����̒ǐՂœ���ꂽ�l�ł��ꂼ��̊댯���͒��悢����Ƃ�����B �I�b�Y��ƍl����ꍇ�� �킩��Ȃ��Ƃ��͋i���L�@�i�����@�Ɠǂݑւ����Ƃ��ɐ������邩�ۂ��i���ƌ�̎���ɉ������i����킵���j�������������L��������̂Œ��Ӂj �O���B���f�̗L�����ƓK�Ȏ�f�Ԋu���������邽�߂̃P�[�X�E�R���g���[�������i���{��A��Ȋw��G�� Vol. 89 (1998) No. 11 P 894-898 �j https://www.jstage.jst.go.jp/article/jpnjurol1989/89/11/89_11_894/_article/-char/ja/ |
��8��@����̌���
���B�ڕW�W�|�P�m�����ǂ̂悤�ȈӖ������̂��̂���������
�W�|�Q��������̘_���\��������ł���
���ȏ���O��P46�`
�m��
���鎖�ۂ��N���邱�Ƃ����҂����x�����i�����j����̂Ɏ��ۂ��N����^�N����Ȃ��̂����ꂩ�Ƃ��āA�m�������̂܂ܒ��Ă��������Ƃɂ͂Ȃ�Ȃ�
���s�@�T�C�R����U���ĂR�̖ڂ��o��(y or n)
�m���@�T�C�R����U���ĂR�̖ڂ��o��(1/6)
�J��Ԃ����s���s���ƕp�x�����͂��̎��ۂ̊m�����������Ă���
������ΏۂƂ����ꍇ���s���J��Ԃ���H�������ȏꍇ���������������߂Â����J��Ԃ����ƌ���
�������߂��Ȃ��ƒP���ɔ�r�ł��Ȃ����i�Čf�F���ȏ�220�j
���s�̌��ʂ͎����Ő������B���Ƃ����Ă��ꂪ��ɐ������i�^�j�Ƃ͌���Ȃ�
���̎��s�ȍ~�ňقȂ錋�ʂ��ł�\����r���ł��Ȃ����i���Ɏ��s���J��Ԃ��Ȃ��ƂȂ炸�@�����o���Ȃ�
�i�̂ɈقȂ錻�ۂ̋N����m���ɂ�������臒l���߂āA�Ȃ��������Ƃɂ��Ĉ�ʐ����咣����X�^�C���j
���ۂ̋N����m�����������Ⴍ�Ă��A���ۂɋN����Ȃ��킯�ł͂Ȃ��B
�Q�l
�f�W�^���G�{�@�����ς̉J� �i�D�y���ݍ��Z�f�U�C���A�[�g�R�[�X�j
�~��܂ʼnJ�������̂Łu�J�������ΉJ���~��v�ƂȂ��Ă��܂�
�m�g�j���������^��������p�@���ڃe�����̓W�~�[�o���́u���߂����v�i�f�C���[�X�|�[�c�j
https://www.daily.co.jp/gossip/2017/04/12/0010088761.shtml
�Q�l
�܂��ɗ��j�I�u�ԁA�I�o�}�哝�̂̔픚�n�q���V�}�K��ɂ������̃e���r���������ʔԑg�Ő����p
http://kabumatome.doorblog.jp/archives/65863513.html
�w���@
����̔ے�����肵�Ęb�������߂āA���̖������������ƂŖ��肪���藧�Ƃ���_�@��������
���ȏ�P46-����O��݂����Ɍ��肷��̂ł͂Ȃ��A���肷�闝�R�E�m�M�����邩��m���߂�@�Ƃ���������
�菇�P�F���������Ă�i�A������H0����ёΗ�����H1�j
�w���@�Ɋ�Â��ؖ������Ă���B
�i�����Ȃ��������ؖ��ł��Ȃ��̂ŁA���̑Η��ł��鍷�����鉼�����̑�����j
�菇�Q�F���蓝�v�ʂ��v�Z����
���̎��ۂ̋N����m�����v�Z���Ă��邱�ƂɂȂ邪�A�p����m�����z�ɂ���Čv�Z�����قȂ�B
�菇�R�F�L�Ӑ��������߂�
�m���I�ɕK�R�Ƌ��R��蕪���Ă���B��ʂɂT���ŕ����Ă��邪�P���̎�������
�菇�S�F�L�Ӑ����Ɣ�r���A���������p�̑�����
��j�A������H0�����p���Η�����H1�̑�
����
��Ԑ���̘b�̉������オ����iP70��P51���r�j
�������肪�������肵�Ȃ���������
����̔ے�ƌ������̂́u����v���u�Ȃ��v�����Đ��E�͗��\����Ȃ���
�Η������i����j�̔ے�͋A�������i�Ȃ��j�ł́i�Ȃ��j�̔��́H�i����@���ĉ����H�j
���������u�S������v�̔��́u�S���Ȃ��v�B������u�D���v�̔��́u�S���Ȃ��v�B�ł��u�����v�̔����u�S���Ȃ��v
�s���S�ȋA�[�@�œ����̂��Ċ댯����Ȃ���
�G���[���N�������Ƃ��O��̋A�[�@�i�Ƃ肠�������_�𑁂��o������̂́j���G���[�@���G���[�����݂���
�G���[���C�ɂ��Ȃ�����̓����A�s���̗ǂ����_�������邩������Ȃ��@���@�J�
�̂ɂ�݂����Ɍ��肷��̂ł͂Ȃ��A����܂ł̃X�g�[���[�����
�������肷��|�C���g�͏���Ɋg����߂��Ȃ����ƂŁA��������͗p�@����萳�����g���܂��傤
�G���[
���ȏ�P215����̉ߌ�i���G���[�j�E�E�E����ĈႤ�Ɣ��肷��m��
����̉ߌ�i���G���[�j�E�E�E����Ĉꏏ�Ɣ��肷��m��
���Q�l��
�������u�����v�Ɣ��肷��m���E�E�E�P�|��
�������u�Ⴄ�v�Ɣ��肷��m���E�E�E�P�|��
���B�x�m�F
�P�jP50���U�̃N���X�̐l����81�l�A���ςP�R�W�D�Tcm�Ƃ����Ƃ��ɁA���ꂼ��S�����ςƔ�ׂ��Ƃ��S�������ƈႤ�ƌ����邩�B�L�Ӑ�����1%�y��5%�Ƃ��Č��肹���P�f�jP50���U�̃N���X�̐l����64�l�A���ςP�S�P�D�Tcm�Ƃ����Ƃ��ɁA���ꂼ��S�����ςƔ�ׂ��Ƃ��S�������ƈႤ�ƌ����邩�B�L�Ӑ�����1%�y��5%�Ƃ��Č��肹��
�⑫
�]�k�w������Љ�l�ɂȂ�ƁA�����Ŕ��f���čs�����邱�Ƃ����߂���V���Ȗ������������܂��B�s���w�j�ȂǏ���ɓV���畑���~��Ă��邱�Ƃ͂Ȃ��̂ŁA�����Ő������Ă��ݎ���Ă��������B
���ȏ��Y���y�[�W ��3�́iP46-51�j �z�t�����Y���y�[�W �S���w�I�����ɂ����铝�v�I�L�Ӑ�����̓K�p���E,�����r��,�D�y�w�@��w�l���w��I�v79,P45-78, 2006 http://ci.nii.ac.jp/naid/110004812630 �z�z�����̂�P50-58 ���B�x�m�F���ꂱ���L�Ӑ����̉��߂��������l����������̂Œ����L�Ӑ����P���őΗ��������̑�����Ȃ�T���ł��Η��������̑� �L�Ӑ����T���őΗ��������̑�����̏ꍇ�P�����Ƃǂ�������肦�� �L�Ӑ����T���Ŕ���ۗ��Ȃ�P���ł�����ۗ� ���蓝�v�ʁi����̏ꍇ��z�X�R�A�j�Řb�����������������₷���Ǝv���܂��B |
��9��@�p�����g���b�N����
���B�ڕW�X�|�P�p�����g���b�N����̊拭��robustness������ł���
�X�|�Qt������s�����Ƃ��ł���
�p�����g���b�N�ƃm���p�����g���b�N
���ȏ�P44���z�̌`��i�ꐔ�j�Ɉˑ����铝�v�ʁi���ϒl�@�W�����E�E�E�ʓI�ϗʁj
���z�̌`��i�ꐔ�j�Ɉˑ����Ȃ����v�ʁi���ʁ@�����l�@�p�[�Z���g�l�E�E�E���I�ϗʁj
���ȏ�P4-7,204
�p�����g���b�N����E�E�E�v���l�̕��z�����K���z�ł��邱�Ƃ�����
���K�m�����@�E�E�EQ-Q�v���b�g
�f�[�^�������ړx�I�ɗp���Ă��̏�������p�[�Z���^�C�������߂āA���̒l���m�����z�i���K���z�j�ɑ�����Ċ��Ғl���Z�o���Ĕ�r����B
P11���G�Ȓ����f�[�^TG��p����
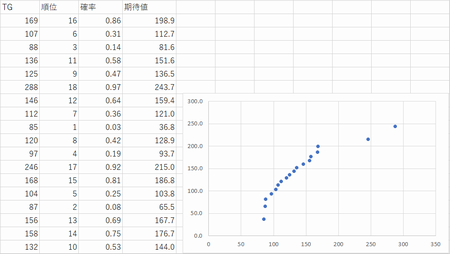
���Q�l�����K�m���v���b�g�̍����i���vWEB�@�Љ���T�[�r�X���v�����������j
https://software.ssri.co.jp/statweb2/tips/tips_8.html
�K�ȓ��v�����ɕK�v�ȍl����
P203-216�E���z�̐��K��
�@������ȂɋC�ɂ��Ă��Ȃ�
�@���z�̐��K���ɂ��āu�f�[�^�����傫���Ȃ�Ɛ����v�E�E�E�ǂ̒��x �@�p�����g���b�N�̏ꍇ�����ǑÓ��Șb�ɂȂ��Ă��܂� �E����@�ɂ���Ĕ��肪�قȂ�ꍇ
�@���f�[�^���o�Ă��猟��@��I������͓̂K�ł͂Ȃ�
�E�Б�����C��������
�@���������肪�Ó�
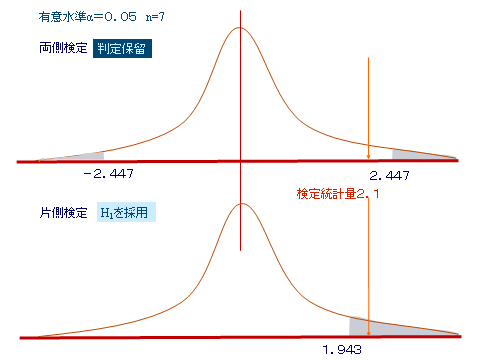
�E�L�Ӎ�����̗L�Ӑ�����0.05�ł悢��
�E�L�Ӎ����肪���Ӗ��ȏꍇ
�@�����v�I�L�Ӎ��ƗՏ��I�L�Ӎ��̘b �@���ȏ��̌��ʗʂɑ���K�v�f�[�^�����ς��������̂��ȉ�
�@�e�Q10�f�[�^�Ō��肷���10kg���x�ƂȂ邪�A�����܂ő̏d���ω����Ă���ƂȂɂ��Ⴄ�o�������N�����Ă���C������
�@�e�Q1000�f�[�^���炢�Ō��肷���1kg���x�ŗL�ӂȌ��ʂƂȂ邪�A�{���ɈӖ�����̂��C�ɂȂ�
�@
�@ �@���Q�l�����̎��Â͗Տ��I�ɗL�v���iPEDro�j
�@https://www.pedro.org.au/japanese/tutorial/is-the-therapy-clinically-useful/
�@���Q�l�����v�I�L�Ӑ���P�l�Ɋւ���ASA����
�@http://biometrics.gr.jp/news/all/ASA.pdf
�@�ȉ��������܂���
�@1. P�l�̓f�[�^�Ɠ���̓��v���f��������������x�����߂��w�W�̂ЂƂ�
�@2. P�l�́A���ׂĂ��鉼�����������m���𑪂���̂ł͂Ȃ�
�@3. �Ȋw�I�Ȍ��_�́AP�l������l�������ǂ����ɂ̂݊�Â��ׂ��ł͂Ȃ�
�@4. �K���Ȑ����̂��߂ɂ́A���ׂĂ���铧�������K�v
�@5. P�l�́A���ʂ̑傫���⌋�ʂ̏d�v�����Ӗ����Ȃ�
�@6. P�l�́A���ꂾ���ł͉����Ɋւ���G�r�f���X�̂悢�w�W�Ƃ͂Ȃ�Ȃ�
�E�f�[�^���傫���ꍇ�͋�Ԑ���̂ق����Ӗ�����B
���ȏ�P6�e�[�u���i�K�p�v���ɂ��g�������j
1�W�{t����E�E�E��2�W�{t����E�E�E�Q�Q�̓����U��
�̈Ӗ��́A�f�[�^���������Ƃ���Ȃ̂Ŗ��ɂȂ�Ȃ�
�Q�Q�̓����U���Ɋւ��ẮA�����O��Ƃ��Č��肪���藧���Ă���̂Łi�ȉ��ɏЉ��i�X�`���[�f���g�́jt�����
���_�A�����U�ł͂Ȃ��ꍇ�ɗp���錟��i�E�F���`��t����j������̂ł����A��������ŏ�����g���������ǂ��Ƃ����b������܂��B
�m���p�����p�����g���b�N�̘b�Ɠ��l�ł����A�ǂ���ł�낤�Ƃ��L�Ӎ����o�Ă邮�炢���m�Ȃ��̂����z�ł͂���܂���
�֘A2�Q�̍��̌���
1�W�{t����
���ȏ�P58P60���8�����Ȃ���
�֘A����Q�Q�i�y�A�j�E�E�E��̌Q���Q�肵�Ă���
�O��̍�������
t�l�i�W�������ꂽ���蓝�v�ʁj�E�E�E�Q�Q�̃y�A�̍��̕��ς�W���덷�Ő��K����������
�A�������͑O��̍����[��
���蓝�v�ʂƗL�Ӑ�������t�l���r����B
2�W�{t����
���ȏ�P82�`�@P84���12�@P87���13������̏ꍇ�́AF����iP86)�œ����U���m�F���Ă���̎菇�ɂȂ�B
��W�{�Ƃ̈Ⴂ�͕��U���Q�킠�邱�Ɓi��W�{�̓y�A�̍����Ƃ�̂ň�j
���̂��ߍ�������
t�l�E�E�E���ꂼ��̌Q�̕��ς̍���W���덷�Ő��K����������
�@
���B�x�m�F
�P�jP11���G�Ȓ����f�[�^���TG�����ʂɂ�鍷�����邩�L�Ӑ����T���Ō��肹���Ȃ�2�Q�̕��U���������Ƃ݂Ȃ��邱�ƂƂ���
�⑫
�����̗]�k�����Ă����u�}�s�v�X�@�W�W�ΓX��A�~�[�œ|�ꎀ���i�����V���jhttps://headlines.yahoo.co.jp/hl?a=20170604-00000015-asahi-soci �E�Ŋ��܂Ō����ł�����Љ� �E�}�s�ł��~�܂�����̂Ɂ������}�~�܂� >Student��t����Ƃ������̗R�����ȏ��ɃL�`���ƍڂ��Ă���Ɗ��Ⴂ���Ă���܂����B�ʂ̖{�ł����B���̋��ȏ����`���b�ƍڂ��Ă���̂ł��̎��Ɍy���b�������悤�ȋC�����܂����iP82�j ���L�̃y�[�W������������ ���v�Ŕ�ꂽ��r�[���Ŋ��t?! �X�`���[�f���g��t����ƃM�l�X�r�[���̊W�i�݂Ă݂Ď����I �S���w�j�@-��17��-�@���{�S���w��j http://www.psych.or.jp/interest/mm-17.html ���B�x�m�F���ꂱ��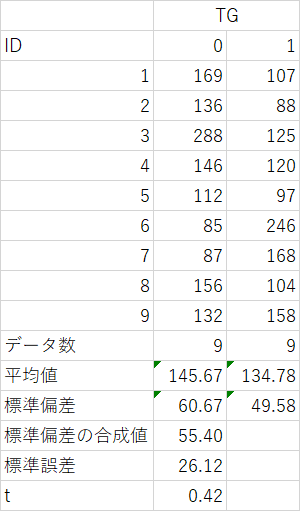 ��݂����Ɍ��肷��̂ł͂Ȃ��A���鉼���������Ă�����ؖ�����̂����画��ۗ��Ƃ���̂��B�������͎�サ���u�����݂��Ȃ�����(�L�E�ցE�M)�v�Ƃ��������� |
��10��@�m���p�����g���b�N����
���B�ڕW�P�O�|�P�p�����g���b�N����ƃm���p�����g���b�N����̈Ⴂ������ł���
�P�O�|�Q�m���p�����g���b�N������s�����肷�邱�Ƃ��o����
��W�{Wilcoxon����
�E�B���R�N�\���̕����t���ʘa�������ȏ��iP6)�E�E�E���z�^�C�v���ړx�C���U�̐���Ȃ�
���ȏ��iP74�j
�P�F�y�A�̃f�[�^�̍�d�����߂�
�Q�Fd�̐�Βl��肻�ꂼ��̍��id�j�̏��ʁi�����j�����߂�
�@�@�����ʂ̘b�E�E�E���ȏ�P76�Q��
�R�F���蓝�v��T�́{�C�|�ʂɏ��ʂ𑫂������̂ŏ�������
�L�ӊm���ɂ��Ă͒��ڌv�Z�o���邪�iP75�j���X�ƌv�Z���Ă����̂͑��
n��25�܂ł�Wilcoxon����\���g���Ă��������iP274)
N�������Ȃ��Ɓi�̕����j����ۗ��ɂ����Ȃ�Ȃ�
���ȏ�P78�Q�Ƃ̂���
n��25�͐��K���z�ɋߎ��ƌ��Ȃ���z�l�����߂���@�Ō���
���ϒl
���ϒl�ƂȂ��Ă��邪���Ғl�i�����l�j��k=n(n+1)/2��1/2
�A���
���ʂ͏����ړx�ŗ��U�����̂܂܈����Ɛ��K���z�ƍ���Ȃ��̂ł��ꂼ��0���Ɍ�������0.5�����V�t�g
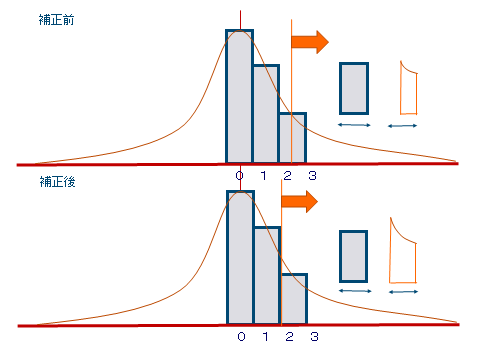
P76(���10)�Q��
Mann-Whitney����
��W�{�ɂȂ�Ƃ�₱�����Ȃ�̂̓p�����g���b�N����Ɠ���P102�Q��
���蓝�v��
���Q�̌X�ɂ��āA����������Q�ő傫���̐��̑��a�����߂Č��蓝�v�ʂƂ��Ă���
�P�F����Q�iA�j�̒l���ꂼ�ꂪ��������̌Q�iB�j�ɓ������Ƃ����Ƃ��ɁiA�́j���̒l�����iB�̌Q�̂Ȃ��Łj�l���傫�������J�E���g����B�iA�Q�́j�S�Ăɂ��čs���a���Ƃ�B�i����-1�̘b�j
�Q�FA��B�����ւ��ĂP�F�Ɠ��l�̌v�Z�����邩�A������B�Q�̘a�����ߏ������������蓝�v��U�Ƃ���
�@�@�����ʂ̘b�E�E�E���ȏ�P103�Q��
��������W�{���������Ȃ�Ɛ��K���z�̘b���o�Ă���
P104���17�E�E�Et����i�E�F���`��t�����P=0.032�j
�i��T��W�{t������s���܂������A���ۂɂ͓����U���ۂ��ɊW�Ȃ��E�F���`��t������s���̂��ߔN�̗���ł��j
�A���{���Ƃœ�W�{t������s���ꍇ�́A���ȏ��I�ȓs��������܂��̂ŁE�E�E�i�d��Ōv�Z����̂���₱�����ł����j
���B�x�m�F
�P�j�V�U���10�ɂ��ăp�����g���b�N������s���A�m���p�����g���b�N����̌��ʂƔ�r����B
�@���K�m�����@
�Q�jP63���K�S�ɂ��ăm���p�����g���b�N������s���A�p�����g���b�N����̌��ʂƔ�r����B
�R�jP84���12�ɂ��ăm���p�����g���b�N������s���A�p�����g���b�N����̌��ʂƔ�r����B
�S�j1�`�R�j�܂ł̔�r���猟���@�̑I���A���ʂ̉��߁A�p���^�m���p���̓����ɂ��čl�@����
�@
�⑫
���B�x�m�F���ꂱ���P�jdbar=8.75 Sd=1.118 t=2.767�Q�j��W�{Wilcoxon����@���蓝�v�ʂ�7.5�@n��10�� �R�jMann-Whitney����@���蓝�v�ʂ�6.5 �����̗]�k���Ƃ����������Ƃ���܂����H���ӂ��܂��傤���Ƃ����ꍇ�Ĕ��s���Ă��ԍ����ς������A�������c��^�C�v������܂� 12���̉^�]�Ƌ��ؔԍ��͉����Ӗ�����̂ł��傤���H�i�݂�Ȃ̒m�� ������ƕ֗����j http://www.benricho.org/drivinglicense/ AI�ɂ܂���̘b ���� �P�S�E���䑏���l�i�A���P�ƂQ�ʂ̂Q�T�A���I�c�S���łT���̉��i���i�X�|�[�c��m�j http://www.hochi.co.jp/topics/20170610-OHT1T50148.html ���𖼐l���R���s���[�^�[�ɕ������B�����d���킪�A�l�ԓ��m�ƈႤ�����B�iNumber Web�j http://number.bunshun.jp/articles/-/827817 �y��Q���d����z����Ŗ��A���l�L�I�̔����ꂸ�@�u��l�̒m�b�Ɋ��Ӂv�u�`�h���������\����Nj��v http://www.sankei.com/west/news/170520/wst1705200089-n1.html �l�ԓ��m�̐킢�̐��E�ł��邱�Ƃ����N���ɂȂ�ł��傤�B ������ �������� �K�[�h���[���ڐG��A���щz�����\���i�����V���j https://mainichi.jp/articles/20170612/k00/00e/040/141000c ���Y�G�N�X�g���C���Ɏ����^�]�@�\�@�Z���i�ɑ�����Q�e�i�����V���j http://www.asahi.com/articles/ASK683SMLK68ULFA00H.html ���ꂩ��掩���^�]�����y���Ă������Ƃł��傤�B�A������̃o�X�������^�]�������Ƃ�����E�E�E �����̎������݂̘b�s���s�ׂƋ^���Ȃ��悤�Ɂ@�̘b |
��11��@�v���l�f�[�^�̌���
���B�ڕW�P�P�|�P���z�Ɛ��K���z�̊W������ł���
�P�P�|�Q�J�C��敪�z�Ɛ��K���z�̊W������ł���
�v�ʒl�ƌv���l
�v�ʒl�E�E�E�ʂ𑪒��v���l�E�E�E�p�x�𑪒�i���`�ړx�j
�ʓI�ϗʂ͕p�x�̑�����o����
���z
�W�{�̑傫��=n���ۂ̋N����m��=p
r=np=n�s���J��Ԃ����Ƃ��Ɏ��ۂ̋N����i���ғx���j
���z��np���T�����傫���in���\���ɑ傫���ꍇ�@���ȏ��ł�np��10 and n(1-p)��10�j���K���z�ɋߎ��iP135�j
�ԂQ�敪�z
���ȏ�P142�ԂQ�敪�z�E�E�E�ꕪ�U�𐄒�ł���m�����z
���R�x�ƂƂ��ɕ��U����������
���K���z����㑤�m�����v�Z
�o���c�L�̘b�Ȃ̂ʼn����̊m���̓o���������Ă��Ȃ��m��
�@���@���K���z�̗���5%�i����2.5%���j�̓J�C���ŏ㑤�ɏW���
���Q�挟��
�o���x��Oi�Ɗ��ғx��Ei�̃Y�����������ғx���͗^����ꂽ��琄���������_�I�ɋ��߂��x��
�Ɨ����͂��ꂼ��̗v����p���Đ���
���ғx�����Ⴂ�ꍇ�A���̂܂g���Ȃ����A�v�Z�͊y
Fisher�̒��ڊm���@�͂��ł��g���邪�v�Z���
�i�R���s���[�^���g���鎞��j
�̂ɋ��ȏ��ł͂Q�~�Q�\�ȊO�o�Ă��Ȃ��i�l�����͈ꏏ�j
�悭����H�ԈႦ
�x���Ȃ̂ɔ䗦�i�P�O�O���j�ɒ����Ă��猟��Ƃ�
���B�x�m�F
�P�j�C�`���[�I��̌����_�i2016�N�x�I�����_�j�ł̃��M�����[�V�[�Y�����Ő���NBP1278���Łi3619�Ő��jMLB3030���Łi9689�Ő��j����B�ŗ���95%�M����Ԃ����߂�B�@���Q�l���v���싅�̐��U�ŗ�3���͎j��24�l�B�C�`���[��1�ʂ���Ȃ����R�́c�c�B�iNumberWeb�j
�@http://number.bunshun.jp/articles/-/827826
�@���Q�l���C�`���[�iWikipedia�j
�@https://ja.wikipedia.org/wiki/%E3%82%A4%E3%83%81%E3%83%AD%E3%83%BC
�Q�j�C�`���[�����ĒʎZ��14053�Ő��i�s�[�g�E���[�Y�̐��U�Ő��i���Ő���4256�j�j�ɒB�����Ƃ��A���{���Ő����d�˂Ă��邩95%�M����Ԃ����߂�
�@���Q�l���s�[�g�E���[�Y�iWikipedia�j
�@https://ja.wikipedia.org/wiki/%E3%83%94%E3%83%BC%E3%83%88%E3%83%BB%E3%83%AD%E3%83%BC%E3%82%BA
�R�jP146���Q�X�̌v���l�����ׂĔ����ɂ��Č��肵���Q�X�̌��茋�ʂƔ�r����
�S�j�ȉ��̎��Ö@�Ɛ������S���̊W���玡�Ö@�ɂ��]�A���قȂ邩���肹��
| ���Ö@A | ���Ö@B | ||
|---|---|---|---|
| ���� | �P�O | �@�W | �P�W |
| ���S | �@�Q | �P�O | �P�Q |
| �P�Q | �P�W |
�⑫
���B�x�m�F���ꂱ�������͂����܂ł��ߋ��̉�������Ŗ���D����ʂ����邱�Ƃ����Ő��̐���Ŏv�����̂ł͂Ȃ��ł��傤���B
�P�j �ώ@�䗦Po���i�P�Q�V�W�{�R�O�R�O�j�^�i�R�U�P�X�{�X�U�W�X�j���O�D�R�Q�R�V �O�D�R�Q�R�V�|�P�D�X�U���i�O�D�R�Q�R�V���i�P�|�O�D�R�Q�R�V�j�^�i�R�U�P�X�{�X�U�W�X�j�j�O�i�P�^�Q�j���o���O�D�R�Q�R�V�{�P�D�X�U���i�O�D�R�Q�R�V���i�P�|�O�D�R�Q�R�V�j�^�i�R�U�P�X�{�X�U�W�X�j�j�O�Q �O�D�R�P�T�W���o���O�D�R�R�P�V �Q�j �P�S�O�T�R�|�R�U�P�X�|�X�U�W�X���V�S�T�Ő� �V�S�T���O�D�R�Q�R�V�|�P�D�X�U���i�V�S�T���O�D�R�Q�R�V�i�P�|�O�D�R�Q�R�V�j�j�O�i�P�^�Q�j�������V�S�T���O�D�R�Q�R�V�{�P�D�X�U���i�V�S�T���O�D�R�Q�R�V�i�P�|�O�D�R�Q�R�V�j�j�O�i�P�^�Q�j �Q�P�U�D�P�������Q�U�U�D�Q �i���Ӂj �o�P�R�U���Q�T�̏ꍇ�́i�P�j�i�Q�j�Ƃ��ɂP�O�O��Ȃ̂ōĔ����̐��肩�炻�̂܂܍Ĕ��Ǘᐔ���o���邪�A������̏ꍇ�͑ŗ��̐���ƈ��Ő��̘b�͑Ő����Ⴄ�̂ł��̂܂܂ł̓_�� �R�j ���Q���R�D�V�T �S�j ���ғx�������߂�� a=7.2 b=10.8 c=4.8 d=7.2 Fisher�̒��ڊm���v�Z�@�ŋ��߂� 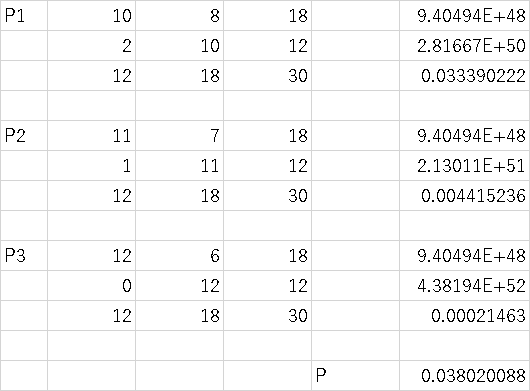
�����̗]�k���̓����Z���t�T�[�r�X�Ŋy���݂܂������A��̓��ŃJ�[�l�[�V�������v���[���g��������ŕ������Ƃ�������͂܂����������Ƃ��Ȃ��ł��B
�ޗLj��̗ǂ��Ƃ���̘b�@�ǂ�����낵�����肢�������܂��B ���B�x�m�F��12��ڂ܂ł̗\�� 13��ڂ̎��Ƃ̎��ɂ���܂ł̒�o��Ԃ��܂��B�ԈႢ�ȂLjًc�̂������14��ڂ�������15��ڂ̎��ƏC����ɗ��Ă��������B |
��12��@�Ɨ����Q�Ԃ̔�r
���B�ڕW�P�Q�|�PF���z�ƃJ�C��敪�z�̊W������ł���
�P�Q�|�Q���U���͂Ƒ��d����̈Ⴂ������ł���
F���z
�J�C��敪�z�Ɠ��������U�Ɋւ���m�����z���ꂼ��̌Q�̃J�C���l�̔䁁���U�̔�E�E�E�e�l�i�e�̓t�B�b�V���[�̂e�j
F���z�ƃJ�C��敪�z�̊W
��^2(��)=�ˁ~F�i��,���j
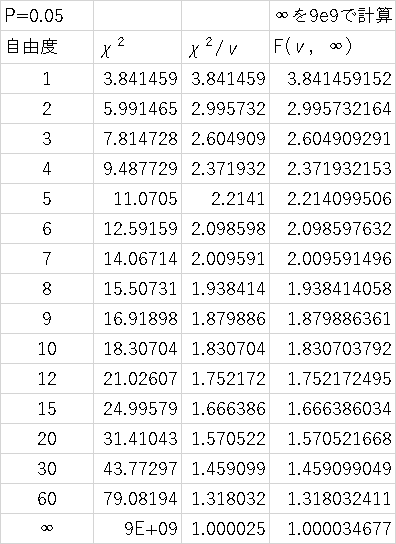
F����̘b
�����U���̌���E�E�E���U������߂�F�l��蔻���u2�Q�̕��U�͈قȂ�Ƃ͌����Ȃ��v�E�E�E�A�����������p�ł��Ȃ��i�ۗ��j
�@ �u2�Q�̕��U�ɍ��������Ƃ͌����Ȃ��Ƃ͌����Ȃ��v�Ƃ������{��ɂȂ�
���Q�l��
�b��́u�����̏ؖ��v���������Đ������Ă݂� �iNAVER�܂Ƃ߁j
https://matome.naver.jp/odai/2136251918746186001
���Q�Ԃ̔�r
���ȏ�P154�Q�����E�E�E�����ړx�ȏ�ł��̊֘A���݂�����������r
�Q�����E�E�E���`�ړxor�֘A������킯�ł͂Ȃ������d��r
������r���č������������瑽�d��r����Ƃ����̂́A�����q�ׂ������ɂ�邪�E�E�E
������r
����܂łƓ����悤�ɐ��K���z�ɏ]�����ۂ��̘b�ɂȂ遨P172�iP111�ƑΔ䂳���Ȃ���j�ꌳ�z�u���U����
�Q�ԕ��U�ƌQ�����U�̔���Ƃ�Kruskal-Wallis����
���ȏ�P164P166���33�̃f�[�^�ŋɒ[�l�̘b
���d����
���ȏ�P217�|�C���g�Ƃ��ẮA���ꂼ��̌��肪�Ɨ����������ɂ��ƂÂ������̂ƍl���ėǂ����ۂ��B�ǂ��̂ł���Α��d����ɂȂ�Ȃ�
��A�̂��̂ł���ΑΗ��������l�����Ƃ��ɗL�Ӑ������T���ƌ����Ȃ���T���ɂȂ��Ă��Ȃ��̂ł́H
���d�Ɍ��肷�邱�Ƃłǂꂩ������A�������͊��p�ł���̂ŗႦ��3�Q�������肾�ƗL�Ӑ���0.05�ő��d����i6�ʂ�j����ƗL�Ӑ�����0.265�ɂȂ��Ă��܂��B�i����悭�Ȃ��j
�L�ӊm����@
Bonferrini�̏ꍇ��6�ʂ茟�肷��̂ł���A�ꌟ�肠����̗L�Ӑ�������0.05/6=0.0083�ƂȂ�B�S�̂ł�1-(1-0.00833)^6=1-0.95103=0.0490Sidak��̏ꍇ�͓��l��1-(1-0.05)^(1/6)=0.008512�@1-(1-0.008512)^6=1-0.95=0.0500
���Q�ɂȂ�قnj��肠����̗L�Ӑ����������遨�����o�ɂ���
���d��r�@
�p�����g���b�N�@Tukey�@�E�E�E�e�y�A�ɑ��镽�ϒl�̍��̌���
Dunnett����E�E�E��̑ΏیQ�Ƃ̑Δ�
�m���p�����g���b�N�@
Dunn�@
���B�x�m�F
�P�jP163���K14��60dB�`80dB�̃f�[�^���ꌳ�z�u���U���͂������ꍇ�ǂ̂悤�Ȍ��ʂɂȂ邩���߂��Q�jP158���31�ɂ���Kruskall-Wallis�����p���Ĕ��肹��
�R�jP171���K16�ɂ��Ĉꌳ�z�u���U���͂�p���Ĕ��肹��
�S�j�j���ʂɌ����̊Ǘ��p�����𑪒肵���B���ꂼ�ꑍ������œ�W�{t������s���B�L�ӊm�������L�Ӑ����T���Ŕ��肵�L�ӂȑg�ݍ��킹�����ׂċL��
�⑫
|
���ȏ�P157 ��@�e���is�`�Q�^�����`�j�^�is�d�Q�^�����d�j ���@�e���i�r�`�^�����`�j�^�i�r�d�^�����d�j �Ə������̂ł����A����A�r�Ƃ������炪���Ă�₱�����������ł��B���̂悤�ɍĒ��� ���@�e��s�`�Q�^s�d�Q ���Ȃ݂� �e���ꂼ��̌Q�̃J�C���l�̔���Ƃ������� ���i���P�Q�^�����P�j�^�i���Q�Q�^�����Q�j ���i���P�Q�^���P�Q�j�^�i���Q�Q�^���Q�Q�j ��W�c���������Ƃ���� �����P�Q�^���Q�Q �����U�̔� ���B�x�m�F���ꂱ���P�j������27.88�r�`���P�O���i�Q�Q�|�Q�V�D�W�W�j�Q�{�V���i�Q�V�|�Q�V�D�W�W�j�Q�{�W���i�R�U�|�Q�V�D�W�W�j�Q �@�@���W�V�W�D�U�S �r�d���P�O�R�Q�|�i�W�P�{�S�X�{�X�{�P�{�S�{�X�{�R�U�{�S�X�j���V�X�S �Q�ԕs�Ε��U���W�V�W�D�U�S�^�Q���S�R�X�D�R�Q �S���ϓ����V�X�S�^�Q�Q���R�U�D�O�X �e�l���P�Q�D�P�V ���d��r�@�̎��͓��Ɂu���������ł͂Ȃ������ۗ��E�E�E�A���������Ȃ��Ȃ����p�ł��Ȃ��Ȃ邩��v ���d����͋A�������̗��ĕ��̖�� �d��̌��i���̂Q�j�ȑO�����������݂Ńv���O���}�u���d��̓_���Ȃǂ̘b�����Ă��܂������A�u�y�n�Ɖ������m�����v���Q�l�Ɏ������݂̉ۂ����߂܂��̂Ŋ���悭�ǂ�ŏ������Ă����Ă��������B �����Q�X�N�x�y�n�Ɖ������m�����̕M�L�����ɂ�����d��̎g�p�ɂ��āi�@���ȁj http://www.moj.go.jp/content/001227288.pdf �Q�l���� ���͖@�̑Ó����m�F�Ɋւ���K�C�_���X�i�_���@�\�j��� http://www.naro.affrc.go.jp/org/nfri/yakudachi/datosei/pdf/F_and_Chisquare.pdf F���z�Ƃ͉����H�i�悤�����A���w�W�������̕s�m�����ւ̂����Ȃ� �i�Y�ƋZ�p�����������j�j https://staff.aist.go.jp/t.ihara/f.html F���z�ɂ��ābExcel�i�G�N�Z���j�Ŋw�ԃf�[�^���̓u���O�i�i���b�W�f�[�^�T�[�r�X�j http://kdsv.jp/news/archives/778 |
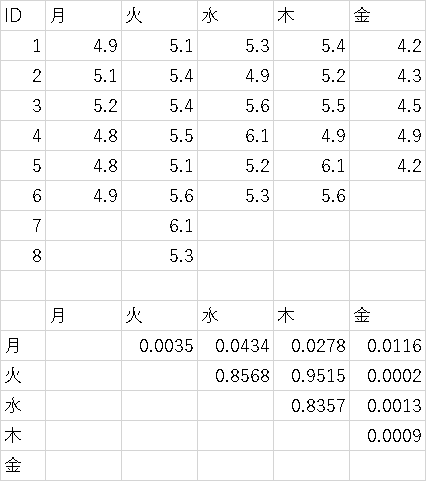
��13��@�������ԕ���
���B�ڕW�P�R�|�P�J�v�����}�C���[�@�ɂ�鐶�������v�Z���邱�Ƃ��o����
�P�R�|�Q���O�����N����ɂ�鐶�����̍��̌�����s�����Ƃ��o����
�������ԕ��͎͂��Ö@���̕]���Ɏ��Ԏ����܂߂�����
�C�x���g�����܂ł̎��Ԃɂ�镪��
������
�������ɂ͌v�Z�����������d�Z�@�̕��y�ɂ��Kaplan-Meier�@�ł��e�ՂɌv�Z�o���鎞��
�����������͔�̓���Ȍ`�ԂŒP�ʎ��Ԃ�����̃C�x���g����\�킷
�i��6��̎��ƂŔ䗦�������グ�܂����j
Kaplan-Meier�ŋ��߂��C�x���g�����i�����j����1-�C�x���g�����i���S�j���́A���ł͖������_�C�x���g�i���S�j�����Ȃ̂Œ���
���Q�l��
���҂̐������i�n�悪��o�^�S�����c��j
http://www.jacr.info/about/survival.html
���ږ@�͊����B���r�ł��肪����ƍ���
�����ی������@�������B���r�ł���ɂ��Ă͂P�^�Q���ώ@���ԂɊ܂߂Ă��邪�C�x���g�����i���S�j�҂̊ώ@���Ԃ��l�����Ă��Ȃ��̂ŗ��ł͖����i�l�����Ă�����l�N������i���j�ɂȂ�j
�J�v�����}�C���[�@�ɂ��C�x���g�������̌v�Z
�[�f�[�^| ����ID | �f�f�� | �Ĕ����� | ����ID | �f�f�� | �Ĕ����� | ����ID | �f�f�� | �Ĕ����� | ����ID | �f�f�� | �Ĕ����� | ����ID | �f�f�� | �Ĕ����� |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | b | 3 | 11 | a | 8 | 21 | b | 9 | 31 | b | 24+ | 41 | a | 3+ |
| 2 | b | 5 | 12 | b | 14 | 22 | b | 18 | 32 | a | 12 | 42 | b | 8 |
| 3 | b | 6 | 13 | b | 9 | 23 | a | 12+ | 33 | a | 3+ | 43 | b | 24+ |
| 4 | b | 14 | 14 | a | 1 | 24 | a | 3 | 34 | b | 13 | 44 | a | 5+ |
| 5 | a | 7+ | 15 | a | 2 | 25 | b | 17+ | 35 | b | 17 | 45 | b | 14 |
| 6 | a | 14 | 16 | a | 3 | 26 | a | 7 | 36 | a | 3 | |||
| 7 | a | 17 | 17 | a | 13 | 27 | a | 8 | 37 | b | 15 | |||
| 8 | b | 21 | 18 | b | 21 | 28 | a | 12 | 38 | b | 13 | |||
| 9 | b | 21 | 19 | b | 16 | 29 | b | 12+ | 39 | a | 21 | |||
| 10 | b | 16 | 20 | b | 24+ | 30 | a | 1 | 40 | b | 18 |
�������헦�̌v�Z
����a| �f�f����̌��� | ���J�n���̐��퐔 | ���ǐ� | ���r�ł��萔 | ���NJ��� | ���튄�� | �ݐϐ��헦 |
|---|---|---|---|---|---|---|
| 1 | 20 | 2 | 0 | 0.100 | 0.900 | 0.900 |
| 2 | 18 | 1 | 0 | 0.056 | 0.944 | 0.850 |
| 3 | 17 | 3 | 2 | 0.176 | 0.824 | 0.700 |
| 5 | 12 | 0 | 1 | 0.700 | ||
| 7 | 11 | 1 | 1 | 0.091 | 0.909 | 0.636 |
| 8 | 9 | 2 | 0 | 0.222 | 0.778 | 0.495 |
| 12 | 7 | 2 | 1 | 0.286 | 0.714 | 0.354 |
| 13 | 4 | 1 | 0 | 0.250 | 0.750 | 0.265 |
| 14 | 3 | 1 | 0 | 0.333 | 0.667 | 0.177 |
| 17 | 2 | 1 | 0 | 0.500 | 0.500 | 0.088 |
| 21 | 1 | 1 | 0 | 1.000 | 0.000 | 0.000 |
| �f�f����̌��� | ���J�n���̐��퐔 | ���ǐ� | ���r�ł��萔 | ���NJ��� | ���튄�� | �ݐϐ��헦 |
|---|---|---|---|---|---|---|
| 3 | 25 | 1 | 0 | 0.040 | 0.960 | 0.960 |
| 5 | 24 | 1 | 0 | 0.042 | 0.958 | 0.920 |
| 6 | 23 | 1 | 0 | 0.043 | 0.957 | 0.880 |
| 8 | 22 | 1 | 0 | 0.045 | 0.955 | 0.840 |
| 9 | 21 | 2 | 0 | 0.095 | 0.905 | 0.760 |
| 12 | 19 | 0 | 1 | 0.760 | ||
| 13 | 18 | 2 | 0 | 0.111 | 0.889 | 0.676 |
| 14 | 16 | 3 | 0 | 0.188 | 0.813 | 0.549 |
| 15 | 13 | 1 | 0 | 0.077 | 0.923 | 0.507 |
| 16 | 12 | 2 | 0 | 0.167 | 0.833 | 0.422 |
| 17 | 10 | 1 | 1 | 0.100 | 0.900 | 0.380 |
| 18 | 8 | 2 | 0 | 0.250 | 0.750 | 0.285 |
| 21 | 6 | 3 | 0 | 0.500 | 0.500 | 0.143 |
| 24 | 3 | 0 | 3 | 0.143 |
����a�F��
����b�F�Ԑ�
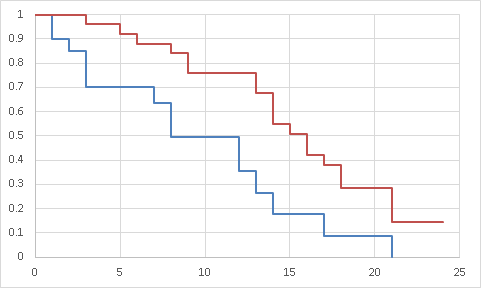
���O�����N����
�J�C��敪�z�ɂ�錟����s���i���ғx���Ɣ�r���ăo���c�L�����邩�ۂ��j
�C�x���g�������̃N���X�\�i�J�b�R���͊��ғx���j
�P����| ���ǐ� | ���퐔 | ���v | |
| �Ǘ�a | 2(0.889) | 18(19.111) | 20 |
| �Ǘ�b | 0(1.111) | 25(24.889) | 25 |
| ���v | 2 | 43 | 45 |
| ���ǐ� | ���퐔 | ���v | |
| �Ǘ�a | 1(0.419) | 17(16.581) | 18 |
| �Ǘ�b | 0(0.581) | 25(24.419) | 25 |
| ���v | 1 | 42 | 43 |
�����늳���y�ъ��ғx��
| �f�f����̌��� | a�ώ@�x�� | a�ł��萔 | a���l�� | a���ғx�� | b�ώ@�x�� | b�ł��萔 | b���l�� | b���ғx�� |
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 0 | 20 | 0.889 | 0 | 0 | 25 | 1.111 |
| 2 | 1 | 0 | 18 | 0.419 | 0 | 0 | 25 | 0.581 |
| 3 | 3 | 2 | 17 | 1.619 | 1 | 0 | 25 | 2.381 |
| 5 | 0 | 1 | 12 | 0.333 | 1 | 0 | 24 | 0.667 |
| 6 | 0 | 0 | 11 | 0.324 | 1 | 0 | 23 | 0.676 |
| 7 | 1 | 1 | 11 | 0.333 | 0 | 0 | 22 | 0.667 |
| 8 | 2 | 0 | 9 | 0.871 | 1 | 0 | 22 | 2.129 |
| 9 | 0 | 0 | 7 | 0.500 | 2 | 0 | 21 | 1.500 |
| 12 | 2 | 1 | 7 | 0.538 | 0 | 1 | 19 | 1.462 |
| 13 | 1 | 0 | 4 | 0.545 | 2 | 0 | 18 | 2.455 |
| 14 | 1 | 0 | 3 | 0.632 | 3 | 0 | 16 | 3.368 |
| 15 | 0 | 0 | 2 | 0.133 | 1 | 0 | 13 | 0.867 |
| 16 | 0 | 0 | 2 | 0.286 | 2 | 0 | 12 | 1.714 |
| 17 | 1 | 0 | 2 | 0.333 | 1 | 1 | 10 | 1.667 |
| 18 | 0 | 0 | 1 | 0.222 | 2 | 0 | 8 | 1.778 |
| 21 | 1 | 0 | 1 | 0.571 | 3 | 0 | 6 | 3.429 |
����͓�̌Q�̔�r�E�E�E���R�xk��n-1=1
�n1��a�ώ@�x���̑��a=15
�d1��a���ғx���̑��a=8.549
�n2��b�ώ@�x���̑��a=20
�d2��b���ғx���̑��a=26.451
���蓝�v�ʃ�^2��6.441
��^2�i1,0.95�j=3.8415
�̂ɋA�����������p���Η��������̑�����ia,b�̍Ĕ����ɍ�������j
�⑫
��14��@���ϗʉ��
���B�ڕW�P�S�|�P���W���ƕΑ��W���̈Ⴂ�𗝉�����
�P�S�|�Q�d��A���͂ɂ����Ăǂ̂悤�ɕϐ����I��Ă��邩�����ł���
���ϗʉ�͂ɂ���
���ȏ�P5�����̕ϗʂ�p���ĒT���I�� ���ށE�\���E�E�E�i�d��A���́j
�v��E�E�E�O�I����Ȃ��i�听�����́j
�u�W���肻���ȃf�[�^���W�߂����ǂǂ�������܂Ƃ܂�̂��v�Ƃ����Y�݂��������Ă���閲�����₷��
�d��A����
���ȏ�P223�i��A�����̘b���v���o�����P��A���́j
��A�E�E�E���ɖ߂�E�E�E���炩�i�藝��W�j�Ɋ�Â��߂��Ă���
�P��A����
���ȏ�P195��A�W���E�E�EY=a+bX��b
�����K��r�͋����U
�P���W���̌���E�E�E�i�L�ӂɑ��ւ����邩�ۂ��j���ȏ�P181���35
���l�� ��A�W���̌���
Ti=b�^SE
���R�x=n-2��t���z
���l�Ɍ���ł���
�r�d���r�p�q�s�i�i�r�����|�r�Q�w�x�^�r�w�w�j�^�i�i���|�Q�j�r�w�w�j�j
�@�@���r�p�q�s�i�i�Q�X�D�T�|�Q�P�O�Q�^�Q�W�j�^�i�i�W�|�Q�j�~�Q�W�j�j �@�@���O�D�Q�W�U Ti=0.75/0.286=2.62
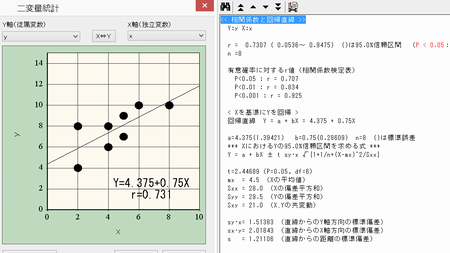
���W���Ɖ�A�W��
��A�����̏ꍇ�͏]���ϐ��ƓƗ��ϐ��̊W��a����b���i��A�W���j�ɕ��������čl�������W���͕����������ɂ��ꂼ��̃o���c�L����ɋ��߂Ă���
X��Y�����ւ���Ɖ�A�W���͕ς��B���W���͕ς��Ȃ��iX,Y�̂ǂ����������邩�Ō덷���ǂ���ɂ���̂��قȂ�j
�Α��W���ƕΉ�A�W��
���֍s��@�P���ւƕΑ���
���ԂƂ��Ă͑��֊W�ō\��Ȃ����A���ꂼ��̕ϗʂ̊W���𖾂炩�ɂ���ɂ͕Α��������̕ϗʂɑ��鑊�ց����֍s��
P184���K17�Ɂi�����Ɂj�N������ĕ��͂���ƁE�E�E�iID1�`5��9�@6�`10��10�@11�`15��11�j
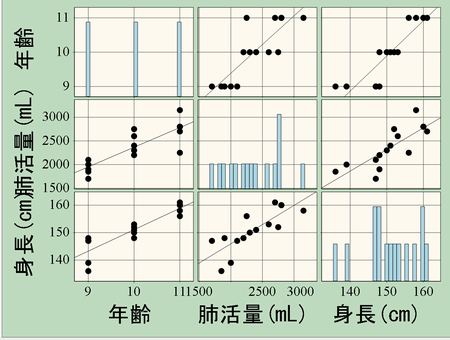
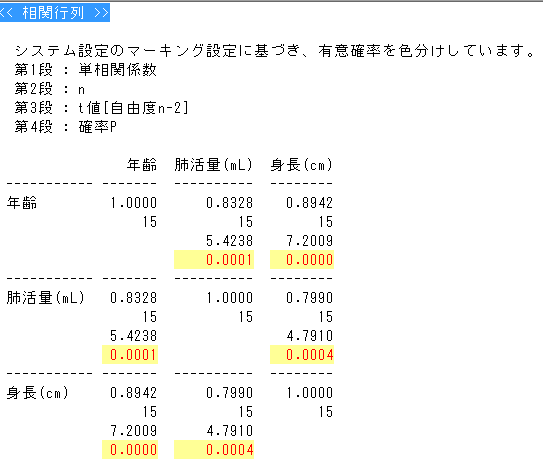
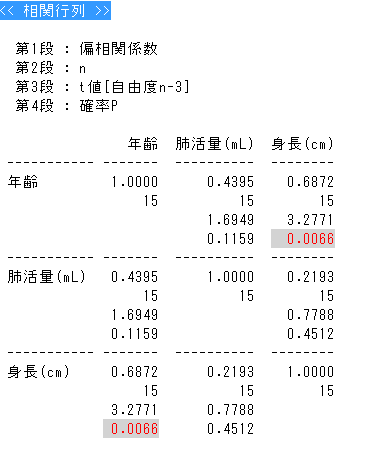
�x���ʂ̘b�Ȃ̂ɁE�E�E
5.2�@�Α��ւƂ́i�A�C�X�N���[��������Ŋw�Ԋy�������v�w�������ւ�����q���͂܂ń����j
http://kogolab.chillout.jp/elearn/icecream/chap5/sec2.html
�d��A���͂̊T�v
Y=b0+b1x1+b2x2+(����)+bnxn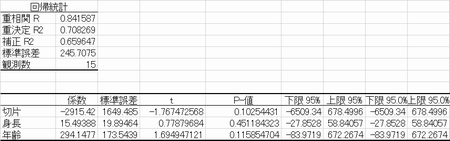
� R2�E�E�E���R�x�C���ς���W���E�E�E�P�ɋ߂��قǗǍD�ȃ��f���B
t�l�E�E�E�W����0���ۂ��̌���
���d������
�ʏ́F�}���`�R�����ϐ��̊Ԃɑ��ւ�����Ƃ��������Ȃ�i��̘b������j
���ւ̂���ϐ�����ɂ܂Ƃ߂�ȂǁE�E�E
�������၄
���� �m�j�@�� �m���Y�C��t�̏A�Əꏊ�̑I��v���Ɋւ��錤���C�G���Љ�ۏጤ�� 45(2), 170-182, 2009
http://www.ipss.go.jp/syoushika/bunken/data/pdf/19114708.pdf
http://www.ipss.go.jp/syoushika/bunken/sakuin/kikan/4502.htm
�R���W���C���g���͂����Ă���B�œK�ȑg�ݍ��킹�����߂�i�����ł͈�t���ǂ̂悤�ȏA�Əꏊ���D�ނ��j
���Q�l��
�Α���v�@Ḏu�a�@�Α��@�F��Y�C�R���W���C���g���͂ɂ��Ă̍l�@�C�ߌ���w�I�v. ��4��, �l���E�Љ�E���R�Ȋw�� Vol.47 page.21-23�C2010
http://library.tsurumi-u.ac.jp/metadb/up/admin/pt4_04_ishimura.pdf
�⑫
�����̘b�i�z�_�j��N�x�̔z�_�͑�̂ł����ȉ��̂悤�Ȋ����ł����O�O�@��1��@�I���G���e�[�V���� �P�T�@��2��@�ړx�E�x�����z �O�U�@��3��@��\�l�E�U�z�x �O�P�@��4��@���ϒl�̐��� �P�T�@��5��@���W���E��A���� �P�U�@��6��@���x�E���ٓx�EROC�Ȑ� �O�S�@��7��@���Ί댯�x �O�O�@��8��@����̌��� �P�O�@��9��@�p�����g���b�N���� �O�P�@��10��@�m���p�����g���b�N���� �P�O�@��11��@�v���l�f�[�^�̌��� �O�P�@��12��@�Ɨ����Q�Ԃ̔�r �Q�P�@��13��@�������ԕ��� �O�O�@��14��@���ϗʉ�� �u�`�����Ă���ƍ��N�x�̏o��̈���킩��̂ł́H�i�ς�镔���ς��Ȃ������j |
��15��@�܂Ƃ�
���B�ڕW�P�T�|�P���Ƃŏo������S�ĉ�����
�P�T�|�Q���C������v�����Ȋw�C����ӗ~������
�����̍ۂ̒��ӎ����ŃJ���[�̍����̘b�����܂������A���̒��Řb�ɂł�tweet�͈ȉ��ł��B
�̂���H�w�n���Ìn�ł́C�������ĂɃJ���[�̍����݂����Ȗ��W�Ȃ��Ƃ������ƕs���i�ɂȂ邱�Ƃ�����D�u����̓������킩��Ȃ������̂ŁC�W�Ȃ����ǒm���Ă鑀�������Ƃ��܂������v��F�߂邱�Ƃ́C�H�ꂪ����������C���҂����S��������Ă������̃��X�N�����߂�����ɂȂ邩��D https://t.co/ljXGJJF9dX
— �쓇 ���F�y���w�z (@TakahikoNojima) 2017�N7��16��