�ޗnj�����ȑ�w�@�������v�w�Q�O�Q�O
�i��w����w�ȁj
���ƃ��j���[�i�c�C�L���X�z�M�̘^���stream�Ō����悤�ɂ��Ă��܂��D[�z�M�O��][�z�M�㔼]���N���b�N�D�j
��1��@�I���G���e�[�V�����@�z�M�O���@�z�M�㔼
��2��@�ړx�E�x�����z�@�z�M�O���@�z�M�㔼
��3��@��\�l�E�U�z�x�@�z�M�O���@�z�M�㔼
��4��@���ϒl�̐����@�z�M�O��1�@�z�M�O��2�@�z�M�㔼�@�ۑ����Ǝ���̗\��
��5��@����̌����@�z�M�O���@�z�M�㔼�@�ۑ����Ǝ���̗\��
��6��@�p�����g���b�N�����@�z�M�O���@�z�M�㔼�@�ۑ����Ǝ���̗\��
��7��@�m���p�����g���b�N�����@�z�M�O���@�z�M�㔼�@�ۑ����Ǝ���̗\��
��8��@�v���l�f�[�^�̌����@�z�M�O���@�z�M�㔼�@�ۑ����Ǝ���̗\��
��9��@�Ɨ����Q�Ԃ̔�r�@�z�M�O���@�z�M�㔼�@�ۑ����Ǝ���̗\��
��10��@���W���E��A�����@�z�M�O���@�z�M�㔼�@�ۑ����Ǝ���̗\��
��11��@���ϗʉ���@�z�M�O���@�z�M�㔼�@�ۑ����Ǝ���̗\��
��12��@���Ί댯�x�@�z�M�O���@�z�M�㔼�@�ۑ����Ǝ���̗\��
��13��@���x�E���ٓx�EROC�Ȑ��@�z�M�O���@�z�M�㔼
��14��@�������ԕ����@�z�M�O���@�z�M�㔼1�@�z�M�㔼2�@�ۑ�i13�C14��j����Ǝ���̗\��
��15��@�܂Ƃ��@�z�M�O���@�z�M�㔼
�O���̔z�M����щۑ莞�Ԃ̊ԃ`���b�g�iteams�j�CLINE���玿��E�R�����g����Ă��������D
�㔼�̔z�M�ł��̓��e�f���ĉ�����܂�
���ƒ��̃��A���^�C���r�f�I�ʘb�͖���������̂Ŏ~�߂܂����D�u�`��̃I�t�B�X�A���[�̊��p�ł�낵�����肢���܂��D
�r�f�I�ʘb��teams�̃`���b�g,zoom,google�n���O�A�E�g�̂����ꂩ�ōs�����Ǝv���܂��D�X���g���ǂ����̂�I�����Ă��������D���͂ǂ�ł�OK�ł��D�i20200420�j�i20200506�ꕔ�폜�j
���Ɣz�M�y�[�W�iTwitcasting @sutolabo�j
https://twitcasting.tv/sutolabo/
��1��@�I���G���e�[�V����
���B�ڕW
�P�|�O�{�Ȗڂɂ�����P�ʎ擾�̈Ӗ������𗝉�����
�P�|�P���v�̌��E�ɂ��ė�������
�P�|�Q�m���ɂ��ė�������
�J�u����ɂ�������
�V�^�R���i�E�C���X������(COVID-19)�̉e���ɂ��I�����C���`���̎��Ƃʍs���܂��D
�]���́u���u���Ɓv�ƌĂ肵�܂����C�F�����w�ߕӂɂ����܂����u�ߗ��Ɓv�ƌĂт܂��傤���D
ICT�̊��p�ɂ��]���Ɠ����悤�Ȋw�C���ɂȂ�悤�C�l���Ȃ���i�߂Ă����܂��D
�I�����C���f�Â͑Ζʐf�Â̕⏕�I�Ȗ����ł����C�����͕ς�邩������܂���D
���Ƃ��Ζʂ�O��Ƀf�U�C�����Ă��邩����C�⏕�I�Ȃ��̂ɂȂ��Ă��܂��܂��D�����Ɍ����ĐF�X�g���C���Ȃ���ł�����낵�����˂������܂�
�F���������ł��邱�Ƃ��]�܂����̂�
�E���ȏ�
�E�l�b�g��
�E�X�}�[�g�t�H��
�p�P�b�g���C�ɂȂ�̂łȂ�ׂ����f���|���Ȃ��悤�ɍl���Ă��܂��D
�u���u�i�ߗׁj���Ɓv�̐i�ߕ�
���O�����P�j���ƌf���ɂ���{�Ȗڂ̎��̃��b�Z�[�W��������������
�Q�j���̃y�[�W�ihttp://www.medbb.net/education/nmubiostat2020/index.html�j�����Ă����悤��
�R�j�R�`���̃��b�Z�[�W�ɃR�����g�t���Ă��������D�����O�͖{���ȊO�D�����Ĕo��ł��Z�̂ł������̊����ꕶ���ł��Ȃ�ł�
�S�j����z�M�̃y�[�Whttps://twitcasting.tv/sutolabo�Ɉ�x�s���Ă����Ă��������D
�@�@�u���E�U�ł�����܂�����낵����Ύ����p�̃A�v��������������������
����
�P�j���̃y�[�W�ihttp://www.medbb.net/education/nmubiostat2020/index.html�j�ɃA�N�Z�X���Ă��������D
�Q�j�R�`�����烁�b�Z�[�W����Ă��������D�����O�͖{���ȊO�D�����č��̋C�����D���ȃX�|�[�c�����ꂩ�����Ă�������
�R�j�݂Ȃ����Ă��瓮��z�M�̃y�[�W�ɍs���܂��D�����ǂ��Ə����Ă��瓮��z�M�̃y�[�Whttps://twitcasting.tv/sutolabo�ɍs���Ă�������
���Ƃ̘A�����@
�E���֘A������A����������
�����ȏꍇ�͑�w�ɂ��₢���킹���������D
�ȉ��Q�Ə��
�y���z�c�C�L���X�A�v���̃f�[�^�ʐM�ʂ�1GB�܂ł̖ڈ��B�ߖ���@�́H�iNetSetsu�j
https://net-torisetsu.jp/twitcasting-traffic/
�{���Ƃ̈ʒu�t��
��w���烂�f���E�R�A�E�J���L�������i����28�N�x�����Łj���x�[�X�ɍ\��http://www.mext.go.jp/b_menu/shingi/chousa/koutou/033-2/toushin/1383962.htm
�{�u�`����w���烂�f���E�R�A�E�J���L�������ɂ����ĒS�������E�֘A�̂��镔��
B�Љ�ƈ�w�E���
�@B-1 �W�c�ɑ�����
�@�@B-1-1) ���v�̊�b
�@�@�@�m���ɂ͕p�x�ƐM�O�̓x�����̓������A�����p�������v�E���v�w�̗L�p���ƌ��E�𗝉����A�m���ϐ��Ƃ��̕��z�A���v�I�����i����ƌ���j�̌����ƕ��@�𗝉�����B
�@�@B-1-2) ���v��@�̓K�p
�@�@�@��w�A�����w�ł悭��������W�{�ɓ��v��@��K�p����Ƃ��ɐ�������_�A���v�p�b�P�[�W�̗��p���܂߂���̓I�Ȉ��������C������B
�@�@B-1-4) �u�w�Ɨ\�h��w
�@�@�@�ی����v�̈Ӌ`�ƌ���A�u�w�Ƃ��̉��p�A���a�̗\�h�ɂ��Ċw�ԁB
�ȉ��̕����͓��v�f�[�^�Řb���o������Ǝv���Ă��܂��D
�@�@B-1-7) �n���ÁE�n��ی�
�@�@�@�n���ÁE�n��ی��݂̍���ƌ���y�щۑ�𗝉����A�n���Âɍv�����邽�߂̔\�͂��l������B
�{���Ƃ̖ړI
�@�������v�w�́A�ی���Õ���ɂ�����ۑ�v�I��@�ɂ�薾�炩�ɂ������Ɏ�����w��ł���B�����ł́A���v�w�̊�b����{����ɂ����Ăǂ̂悤�ȓ��v�I��@���p�����Ă����̂��������A�f�[�^�̎��W�E��́E���ʂ̉��߂ɕK�v�Ƃ�����b�m�����C������B�{���Ƃ̓��B�ڕW
�O�j���v��@�ȂǕK�v�ɉ����āu������Ώo����悤�ɂȂ�\�́v���l�������P�j�f�[�^�̐����Ɋւ��Đ����ł���
�Q�j��{�I�ȓ��v�w�W���Z�o�ł���
�R�j���v�I����𗝉������{�ł���
�S�j���v�I����𗝉������{�ł���
�T�j�f�[�^����舵����ł̒��ӓ_������ł���
���ȏ�
�V�œ��v�w�̊�b ��2��http://www.nikkyoken.com/catalog/catalog_education/642
�Q�l�}��
���ƒ��ɏЉ�܂��Q�l����
�K�v�ɉ����ēK�X�z�z���܂����Ȃ�ׂ��z�z�����ɍςނ悤�ɏo������Ǝv���Ă��܂����Ƃ̐i�ߕ�
�d��g���܂��̂ł�낵�����肢���܂��i���ƒ��̓X�}�z�ł��܂��܂���B�����͂ǂ����悤���l�����j
�P�ʔF��
����u���Ɖۑ�v�����{���܂��B��N�܂ł͎��ōs���Ă��܂������{�N�x�͓����̊ԃf�W�^���Œ�o���������܂��B�ۑ�ɂ��ďW�v�������̂�w�K�w����F�ŋ��L�����ق����ǂ����̂ɂ��Ă�Web��ɏo������ƍl���Ă��܂��D
���ӂ���Ȃ����ɂ��܂��Ă͎��܂Ő\���o�Ă��������D�]���ɂ͈�؊W�Ȃ��̂ł����S���������D
���ƁC�ݖ�ɊW�Ȃ����ǂق̂ڂ̂������e�����X�o������Ǝv���Ă��܂��D
����܂ł̍u�`�ł̗�



���v�͂���W�c�̑S�̑�����������璭�߂Ă��邾���C���̎��_�����
���̒n�}���炱�̎w�E�͂���ǂ��v���܂����D�R�A�o�g�̎��́C�����R�n�̕ǂ͌����I�i����̎R�z���ւ̓��͉����j�ȂǂƎv���Ă��Ƃ����
�]�����@�̓V���o�X�̂Ƃ���ł��D���ׂĎR�z�V�����Ђ���̒�ԉw�̓s�s�chttps://t.co/jdvwNsk9BT
— �X �M�F�iMORI Kunihiko�j (@morikuni_net) April 7, 2020
�G���g���[���邱�ƂƏo�Ȃ��邱�Ƃ͈قȂ�
— �߂ǂԂ� (@medbb) 2019�N4��4��
Donabedian�̒����Â̎��̕]���E�E�E�u�\���v�u�ߒ��v�u���ʁv
�{���Ƃł�
�\���E�E�E�u�`���s�����i��u�Ɋւ���S�̕]���j
�ߒ��E�E�E���B�x�m�F�̏i��u�Ɋւ���ʕ]���j
���ʁE�E�E�����i�X�j
�ƒ�`���܂����B
���ʂ̎w�W���F�X
�Q�l�F��Â̐��ʂɊւ���w�W�i�A�E�g�J���w�W�j�y�щߒ��Ɋւ���w�W�i�v���Z�X�w�W�j�̎戵���i��Ï��̒̂�������Ɋւ��錟����i��W��j�����J���ȁj
http://www.mhlw.go.jp/stf/shingi/2r9852000001u0or-att/2r9852000001u0tr.pdf
���v�̐��E�̘g�g��
�L�q���v�Ɛ������v�ɕ��ނ�����L�q���v�Ƃ�
�E���W�����f�[�^��v�Ă��̏W�c�̏�\���E�����ɂ���f�[�^�͑S�́i��W�c�j
�E�x���i���z�j�E��\�l�E�U�z�x�E���W���Ȃ�
�������v�Ƃ�
���ۂ̋N����m�������肵����őS�́i�ߋ��E���݂����ł͂Ȃ��������܂ށj�𐄑�����B����ƌ���ɕ��ނ����B����Ƃ�
�E���W�����f�[�^����ɂ��Ă��̏W�c�̏�\���E�����ɂ���f�[�^�͈ꕔ�i�W�{�j
�E�_����E��Ԑ���E���f�����O
����Ƃ�
�E���W�����f�[�^����ɂ��Ă��̏W�c�̏�����ɏ]����yes/No�Ŕ��f�����E�����ɂ���f�[�^�͈ꕔ�i�W�{�j
�Et����E�J�C��挟��Ȃ�
��W�c�Ƃ�
�ΏۂƂ��Ă���W�c�̑S�̂��w�������Ƃ��Ɂu��v���ŏ��ɕt����B������W�c�ƗL����W�c����Ȃ�B
�Ώۂ��L���������ɑ��B���邩�̈Ⴂ
�W�{�Ƃ�
��W�c�̈ꕔ�B�����W�{���v�������ׂ�ƁA��ɒ��ӂ���K�v�����邱�Ƃ͎����B
�Q�l
�W�{�����̓T���v�����o�����iThe Huffington Post Japan�jhttp://www.huffingtonpost.jp/nissei-kisokenkyujyo/sample-survey_b_5878832.html
���v�����ɂ���
�W�c����X�̃f�[�^���Ƃ�܂Ƃ߂Ď����̂ŁE�E�E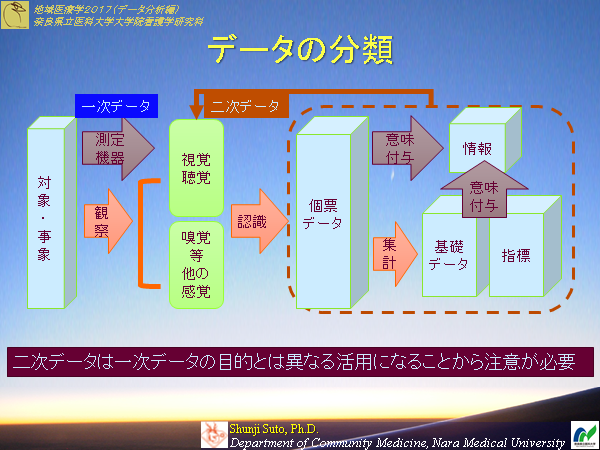
�i�ޗnj�����ȑ�w��w�@�Ō�w�����ȁ@�n���Êw�i���S�F�f�[�^���͕ҁj�@���j
�f�[�^�͖ړI�ɉ����Ċۂ߂�������肵�Ă��܂��B�̂ɓ��p�̏ꍇ�͒��ӂ��K�v�B
�Ƃ肠�������W���ăf�[�^�x�[�X�\�z�����邱�Ƃ��ړI�Ȃ�A���͂͊��ɓ��p�B�ς�����f�[�^��ڎw���Ȃ���ΈӖ�������
�E�ꎟ�f�[�^�͏����_�C���N�g�Ɏ擾����̂ŗ��x��ړI�ɂ��킹�ăR���g���[�����Ă���
�E�f�[�^�͖{���̖ړI�ƈقȂ�f�[�^���p�ƂȂ�̂ŁA���̖ړI�ɑ��ăf�[�^�̗��x������Ȃ���������i�ׂ����ꍇ�͑e���ł��邪�e�����̂͐��肷�邵���Ȃ��j
��Ï��w�̕���͓��p���e�[�}
���Ƃ��Ε��ϒl�̘b
���ς͈�̎w�W�ł����ČX�͎��R�ɂӂ�܂����ʂɉ߂��Ȃ����C���ɉߏ�K�����悤�Ƃ���ƁE�E�E1980�N��㔼��2010�N��O���̂Ƃ����Ђ̓��Ў����r����ƁA����̗���ŋK�i�i�����������Ă���悤�c�l�X�Ȕw�i������H (Togetter)
https://togetter.com/li/1334360
�f�[�^�i���j�ɂ��Ӑ}�����Ƃ��������Ƃ�鎞��Ȃ̂�������Ȃ�
01���Ɖۑ�
�P�j�i���\���Ă��ǂ��͈͂Łj��Ԋm���̒Ⴂ�Ǝv���鑘���������Ƃ̂���o�����͂Ȃ�ł����H���̊m���͉������炢�̏o�����������Ǝv���܂����H�B�Q�j�i���\���Ă��ǂ��͈͂Łj���ςɘf�킳�ꂽ�ȂƎv���o��������܂����H����ǂ̂悤�Ȏ��ł����D�������͕��ςɋ~��ꂽ���Ɓi���\���Ă��ǂ��͈͂Łj�����Ă�������
�R�j�{���̉��u�i�ߗׁj���Ƃ̗ǂ������_�ƈ��������_�i�]���ɂ͉e�����܂���̂Łj
�S�j������c�C�L���X�z�M�ŗǂ��ł����H
�T�jteams�̂ݓ����E�E�P�@teams+slack�E�E�Q�@slack�̂݁E�E�E�R�@�@�Ȃɂ�����ĂȂ��E�E�E0
���ƌ�⑫
��2��@�ړx�E�x�����z
���B�ڕW�Q�|�P�f�[�^�̎ړx���ށi�S�̎ړx�j�ɂ��Đ����ł���
�Q�|�Q�x�����z�\���쐬�ł���
��W�c�ƕW�{�̕⑫
��W�c���璊�o���ĕW�{�����Ƃ��C�C�����Ȃ��ƕ�b����28�N�i2016�N�j��t�E���Ȉ�t�E��t�����̊T���i�����J���ȁj
https://www.mhlw.go.jp/toukei/saikin/hw/ishi/16/index.html
�n��݁C�f�Éȕ݂̘b
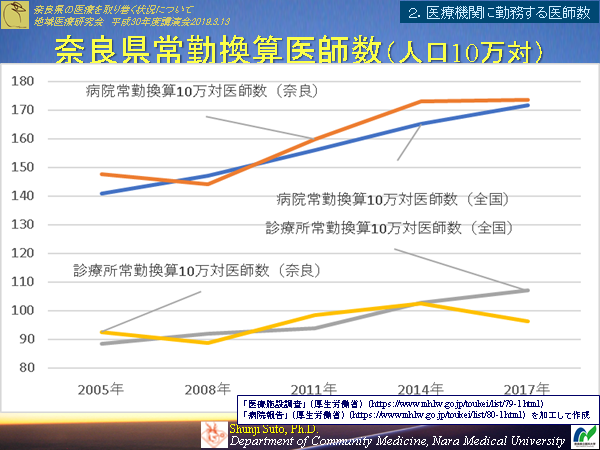
�i�ޗnj��̈�Â���芪���ɂ����@���j
�ϗ�(�f�[�^)�̕���
�ϗʂ͗l�X�Ȃ��̂����邪�����̐������Ƃ�܂Ƃߕ��ނ��邱�Ƃ��o����B���ꂼ����ړx�ƌĂсA4�ɕ��ނ���̂���ʓI�ł���
�P���ގړx�i���`�ړx�j
�Q�����ړx
�R�Ԋu�ړx
�S��ړx�i���j
�P�C�Q�����I�ϗʁi�萫�I�j
�R�C�S��ʓI�ϗʁi��ʓI�j
�����Ƃ��Ă͏�ʌ݊���������
�S���R���Q���P
���ȏ��͊Ԋu�ړx�y�є�ړx�Ɋւ��ē��v�������ʂ���Ӗ��͖����ƂȂ��Ă��邪�A���ӂ͕K�v
�|�C���g�͐��w�I�ɂ͐����������Ƃ��Ă��Ӗ��I�ɐ��������ǂ���
�x�����z�\
���ꂼ��̃f�[�^�i�ϗʁj�̐��i�o���p�x�j���܂Ƃ߂������ϗʂ����`�ړx�̎��͑������i����@�Ƃ��āB�A�����̑����o���Ȃ��ԍŌ�j
�����ړx�ȍ~�ł���Ώ��i���`�ړx�ł���r�̂��߂ɂ���@��j�邱�Ƃ͂���j
�x���@�@�E�E�E�o���p�x
���Γx���E�E�E���o���p�x��1�i100%�j�Ƃ����Ƃ��ɁA���ꂼ��̓x�������߂銄��
�ݐϓx���E�E�E��ʂ̕ϗʂ̓x�������킹���x��
�ݐϑ��Γx���E�E�E�ݐϓx���̑��Δ�
���ȏ�P11�́u���G�Ȓ����f�[�^�vTG�̓x�����z�\���쐬���Ă�������
���Q�l�� �g���O���Z���h�i�s�f�F�������b�j�\���b�̎听���A�얞�̎w�W�\�i���v���c�@�l �_�ސ쌧�\�h��w����j
http://www.yobouigaku-kanagawa.or.jp/kensa/kensati09.html
| �K�� | �K���l | �x�� | ���Γx�� | �ݐϓx�� | �ݐϑ��Γx�� |
|---|---|---|---|---|---|
| 75�`100 | 87.5 | ||||
| 100�`125 | |||||
| 125�`150 | |||||
| 150�`175 | |||||
| 175�`200 | |||||
| 200�`225 | |||||
| 225�`250 | |||||
| 250�`275 | |||||
| 275�`300 | |||||
| �v | ----- | 18 | 1.00 | ----- | ----- |
�x�����z�}
�x�����z���c�_�O���t�Ŏ����������ʓI�ϗʂ̏ꍇ�u�q�X�g�O�����v���c�_�̊Ԋu�͖����i�ʂ�����j
�_�O���t�̖ʐς����̓x���̗ʂ������B�����镔�������K������{�ɂ����ꍇ�x���͔����ŕ`��
��F
�i��1��@�I���G���e�[�V�����@�ޗnj�����ȑ�w�@�������v�w�Q�O�P�V�i��w����w�ȁj�@���j
�{���̉ۑ�
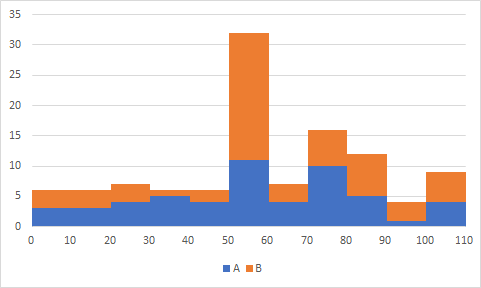
�P�j�z�z�����[�f�[�^���x�����z�\������������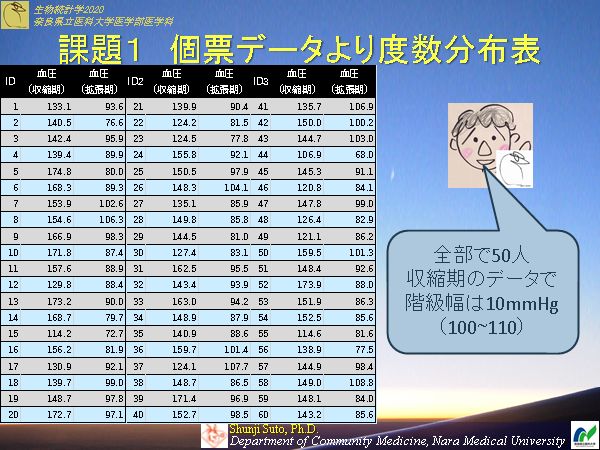
�Q�j���L�̓x�����z�\�̋�A,B,C�����߂�
| �K�� | �K���l | �x�� | ���Γx�� | �ݐϓx�� | �ݐϑ��Γx�� |
|---|---|---|---|---|---|
| 0.5�`1.0 | |||||
| 1.0�`1.5 | 6 | A | 0.325 | ||
| 1.5�`2.0 | 0.1 | 17 | |||
| 2.0�`2.5 | B | 0.65 | |||
| 2.5�`3.0 | 7 | ||||
| 3.0�`3.5 | 0.125 | C | |||
| 3.5�`4.0 | |||||
| �v | ----- | 1.00 | ----- | ----- |
�O�̏ꍇ�̓f�[�^�W�v�̒i�K�ŏ��O����̂Ō��J���Ɋ܂܂�܂���
�P�̏ꍇ�͌ʗ�͒��܂���
�Q�̏ꍇ�͎�����l�����ł��鋰��̂��镔���͍폜���Ē�
���ƌ�⑫
|
0.5�`1.0�@�͂��̎��Ƃł�0.5�ȏ�1.0�����@�œ��ꂵ�܂� �ȉ��̎Ԃ̃L���b�`�R�s�[���v���o���܂� ������CM�̃L���b�`�R�s�[�́u�F�B�ȏ���l�����v�g���^�̃T�C�m�X�R���o�[�`�u���Ƃ����N���}�iOPENcar���{�j https://www.opcar-lab.com/column/sinos_convertible-more-than-friends/ |
��3��@��\�l�E�U�z�x
���B�ڕW�R�|�P��\�l�̎Z�o�y�ѓ����ɂ��Đ����ł���
�R�|�Q�U�z�x�̎Z�o�y�ѓ����ɂ��Đ����ł���
���ȏ�P20-31
��\�l�ƎU�z�x�Ƒ傫��n�i���⎖�ې��j�������A���̏W�c���ǂ�Ȃ��̂��z���o����i�}���\�������j
��\�l
average�i���̏W�c�łƂ�܂Ƃ߂��f�[�^�𐔒l��ŕ\���Bexcel��average���ŎZ�p���ς��o�����A��\�l�̑�\�Ƃ������Ƃ�����Ɖ��߂��Ă��܂��j�Z�p����
mean�i�Z�p���ψȊO�ɂ����敽�ρi�ς��ėݏ捪���Ƃ�j�Ȃǂ�����܂��j1/n�E��xi
�p���[�g�̖@���i80-20�̖@���j
��\�l�Ȃ̂Ɏ��݂��Ȃ��ꍇ������@���@�W�c�̎w�W�i�d�S�j�ł����āA���ۂ��\����l���̂��̂������Ă���Ƃ͌���Ȃ�
��蓹
���ԋ��^���ԓ��v2015�i���Œ��jhttp://www.e-stat.go.jp/SG1/estat/GL08020103.do?_toGL08020103_&listID=000001159883&requestSender=dsearch
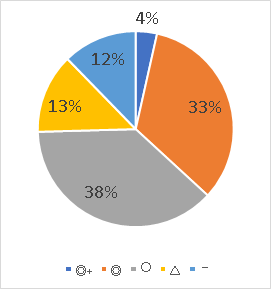
��9�\�@�Ǝ�ʋy�ы��^�K���ʂ̋��^�����Ґ��E���^�z ��� ���[�����c�Ȑ�
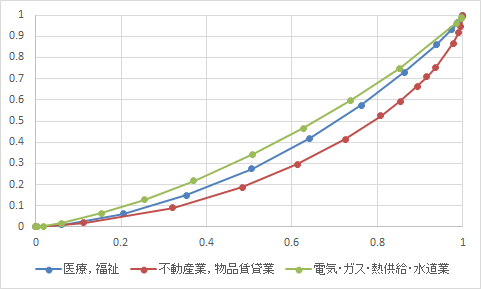
�W�j�W���͈�ÁC����0.358�@�s���Y�ƁC���i����0.439�@�d�C�E�K�X�E�M�����E������0.230
���Ȃ݂ɓޗnj��̈�t�݂̘b�ŋȐ���`���Ɓi�s�����P�ʁj
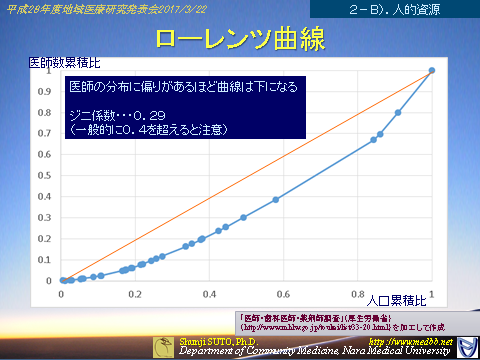
�i�f�[�^���͂���l����n���Ẩۑ��@���j
�����Ƃ��n��ʈ�t���݂̘b�������������ׂĂ����������킯�ł��Ȃ��ł����A�͈͂����߂Ă����قǕ݂͐�����킯�ł�����E�E�E
���\�[�X�̒n���I�ȕ���[���ɂ��邱�Ƃ��̂��͖̂ړI�ł͂Ȃ������ɋ߂Â���i�ł����āA�ɂȂ�ׂ��肪�łȂ��悤�Ȕz�����ł���d�g�݂Ƃ̃p�b�P�[�W�ƍl���Ă���܂�
���d����
�d�݂Â�����������1/n�E��mixi
���p�@�x�����z�\����ɂ������ϒl�̌v�Z�@
���i�K���l�~�x���j�^�ϑ���
�����l
median�i�ʖ���Q�l���ʐ��j�ʓI�ϗʂ������ړx�ŏ���������\�l
���Ԃɕ��ׂ��Ƃ��^�̏��ʂɂ����̂̒l
�̐��������̎��͐^��2�̐��l�̕��ϒl
�X�L�[�W�����v�̔�^�_�͒����l�I�ȃm���ŎZ�p���ς��Ă���
�X�L�[�W�����v��m�낤�I�I���[������i�W�����v��O�~���N�j
https://www.meg-snow.com/jump/rule/rule.html
�ŕp�l
mode�i���s�C�͂��j�Ⴄ�Ӗ��Ő��̗��_�i�������j�̐��E
�ʓI�ϗʂ𖼋`�ړx�ŏ���������\�l
���`�ړx�ł킩�邱�Ƃ͈ꏏ���Ⴄ��
�K�����ɓx�����J�E���g
��ԑ����Ƃ���̊K���l
��ʂ����_�̎��͕��L�i���ς��Ƃ�Ɓ@�����I���D���I�H��ԂɂȂ�j
�U�z�x
dispersion�ő�l�ƍŏ��l���g��
�ő�l�ƍŏ��l���킩����̏W�c�̃o���c�L���킩���ő�lmaximum excel max��
�ŏ��lminimum excel min��
�͈�
RangeR=�ő�l�|�ŏ��l
����
�@�O��l���Ђ炤
�@�Z�o���p��
�l���ʐ����g��
Quartile���������i�����j�ɕ��ׂďW�c��4����
�l���ʔ͈�
IQR(interquartile range)IQR=Q3-Q1
�l���ʕ�
QD(Quartile Deviation)QD=IQR/2
�͈͂͏W�c���O���猩���o���c�L���C���[�W
���͏W�c�̓����̂���l����̃o���c�L���C���[�W
���ϒl���g��
mean��
Deviation���Ƃ��Ƃ͕W���ƂȂ鐔�l����̃Y���i��j���Ӗ�������̂������v�̐��E�ł͏W�c�̕��ϒl����̃Y��������
���̕��ς��Ƃ�ΏW�c���̊e�X�̃Y�����Ղ肪�킩��@���@���v�͏�ɂO�@�̂ɕ��ς���ɂO
���U
varianceV�@excel����VAR
�����悵�����̂̕���
�W����
Standard Deviation�L���͕W�{�W����s�@��W������
s=��V
�i�̂�V��s^2���^2�ŕ\������j
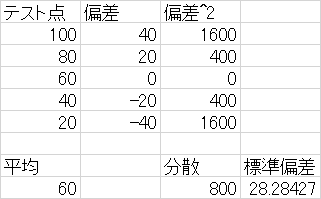
�{���̉ۑ�
�P�j��T�̉ۑ�P�̎��k�������̕��ϒl�����߂��Q�j��T�̉ۑ�P�̎��k�������̓x�����z�\���畽�ϒl�����߂�
�R�j�i�Z�p���ρj�Ɓi�x�����z�\���狁�߂����ρj�͖w�ǂ̃P�[�X�ň�v���Ȃ��D�����鍷�͗��_��ŏ��łO�����A�ő�łǂ̒��x�قȂ邩��������
�S�j���ϒl��3.3�C�����l��3.5�C�ŕp�l��1.5�ƂȂ�悤�ȉ��̓x�����z�\�̋iA)�C(B)�C�iC)�����߂�
| �K�� | �K���l | �x�� | ���Γx�� | �ݐϓx�� | �ݐϑ��Γx�� |
|---|---|---|---|---|---|
| 0.0�`1.0 | 0.5 | 3 | |||
| 1.0�`2.0 | 1.5 | 5 | |||
| 2.0�`3.0 | 2.5 | (A) | |||
| 3.0�`4.0 | 3.5 | (B) | |||
| 4.0�`5.0 | 4.5 | (C) | |||
| 5.0�`6.0 | 5.5 | 3 | |||
| 6.0�`7.0 | 6.5 | 3 | |||
| �v | ----- | 25 | 1.00 | ----- | ----- |
���ƌ�⑫
�{���Љ���b
|
��4��@���ϒl�̐���
���B�ڕW�S�|�P�W�����ƕW���덷�̈Ⴂ������ł���
�S�|�Q�ꕪ�U�����m�̏ꍇ�ł��ꕽ�ς���Ԑ���ł���
���ȏ�P32-40,52-53,70-73,270-271
����
��W�c���璊�o�����W�{����ɕ�W�c�̕��z�������l�i�ꐔ�j�𐄑������_����Ƌ�Ԑ��肪����
�_����
��̒l�Ő����ꕽ�ς̐���l�͕W�{����
�ꕪ�U�̐���l�͕s�Ε��U
��T�̘b�@���ȏ�P22-23�Q��
��Ԑ���
�ꐔ������m���œ��镝������������l�{���̖ڕW��P70�̘b�𗝉����邱�ƁB�ꕽ�ς͈��Ȃ̂ɕW�{���ς͕W�{���ɈقȂ�̂ŕ�����������
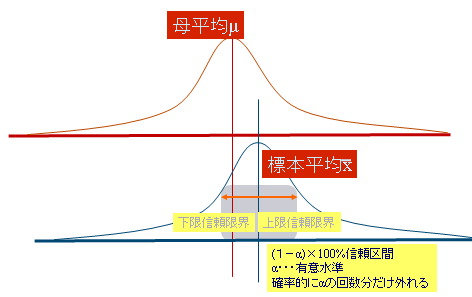
�W�{���ςɕ����������邱�ƂŁA���̘g���ɕꕽ�ς�����B�����ϒl�̃o��������W���덷�@SE=��/��n
�W�����ƕW���덷
�i���ȏ�P52�j�E�W�����͕W�{�̕��z�̃o���c�L�������������
�E�W���덷�͕�W�c���璊�o�����W�{�̕��ϒl�̃o���c�L�
SE=�Ё^��n
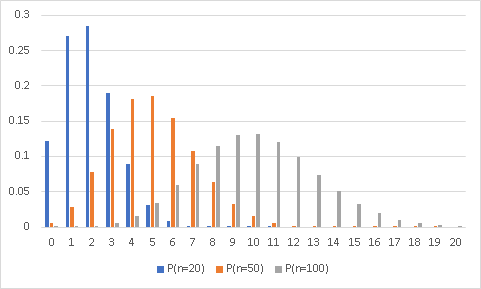
���K���z
���E�Ώ̂̒ޏ��z�i���ȏ�P32-40�j���ϒl�ɋ߂��قǏo������������������ɏ]���ĒႭ�Ȃ�i���Ƃ������j
���������������ŌJ��Ԃ��Ɛ��K���z�ɂȂ�Ƃ����b�����S�Ɍ��藝
�u�َ��ȏW�c�̌v���l���g�ݍ��킳�������z�͐��K���z�ƂȂ�Ȃ��v�i���ȏ�P33�j
���K���z���ۂ��`��̔��f��P28�@�c�x�@��x���Q��
���ȏ��ɂ͌���\�����Ă���܂����i�܂����ƂŌ���̘b�͈���Ă���܂���̂Łj�E�E�E������̋@���
���肷��Ƃ��ɂ́u���z�̐��K���v�Ɋւ��ăf�[�^�����傫����ΐ���Ȃ��Ȃ̂ŁiP6�j�A���܂�C�ɂ��Ȃ��Ă��E�E�E
���S�Ɍ��藝
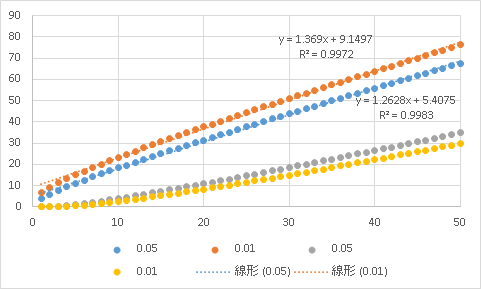
�W�{�̑傫�����\���ł���ΕW�{���ς̕��z�͐��K���z�@�����������肳��Ă���̂ł�����R�덷�̔����͐��K���z�ɏ]��
�@������𑝂₹�Α��₷�ق�
�^�x�Ɛ��x�̘b�i�덷�j�ɒu�������

���K���z�̘b�͐��x�̘b�B�E�ɍs���قǁi���x�������Ȃ�قǁj�L����
�������ϓ��Ƀo�����͂��ł����Ă����s�����Ȃ��Ƃ���Č����邱�Ƃ�����
0����49999�܂ł̗�����XY���W�������v���b�g�P����
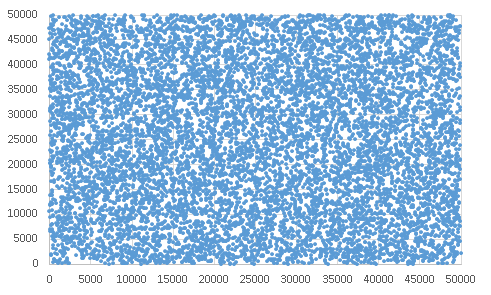
0����49999�܂ł̗�����XY���W�������v���b�g���
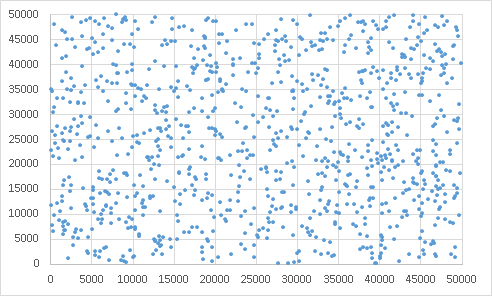
0����49999�܂ł̗�����XY���W�������v���b�g�S��
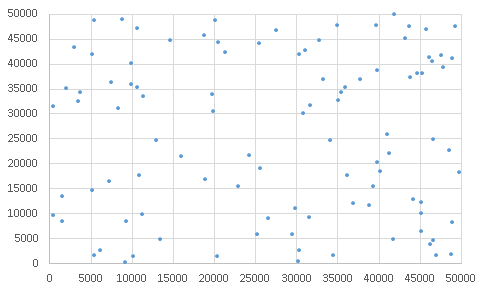
�W�����K���z
���ϒl���O�W�������P�i���U���P�j�ɂȂ�悤�ɒl��ϊ���������
���l�͕��ϒl��50�A�W�������P�O�ɂȂ�悤�ɒl��ϊ���������
���҂̊W
���l=50+10�~z
��W���������m�̏ꍇ�̋�Ԑ���
�i���ȏ�P70�j���K���z�\�łȂ�1.96�ɂȂ�̂��m�F
��W���������m�̏ꍇ�̋�Ԑ���
�i���ȏ�P70�j���K���z�͕ꕽ�ϒl�ƕ�W������������Ȃ��Ǝg���Ȃ���n�������ꍇ�W�{���ςƕW�{�W�����i�s�ΕW�����j�j�ŋߎ��ł��邪
n�����Ȃ��ꍇ�͋ߎ��ł��Ȃ���t���z(�W�{�̎��R�x�˂����킩���Ă���A��͌��蓝�v�ʂ����߂�Ίm�����킩��)
�����z
P64-66
���R�x�݂̂ł��܂�m�����z
���R�x�E�E�E�W�{�̒��Ŏ��R�ɐU�镑�����Ƃ�������Ă���̂̐�
�@�@�@�@�@�@���v�ʂ��ꐔ�̐���ƂȂ�ƁA���R�ɐU�镑���Ȃ��̂��o�Ă���i���܍��킹�j�iP73�j
�W�{���U�͕����a���̂̐��ŏ����邱�Ƃŋ��߂邪�ꕪ�U�̂قǂ悢����ł���s�Ε��U��n-1�i���R�x�j�ŏ�����
���K���z�Ƃ̊W���m�F
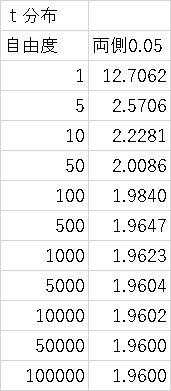
��P70���ēx�m�F
|
���̋��ȏ��ł͕�W���������m�����m���ɂ���Ă̂ݕ����Ă��܂����C�W�{�T�C�Y���傫����Ζ��m�ł����Ă����K���z���g���Đ��肵�Ă�����̂�����܂��D �Ⴆ��30�ȏ�ŕW�{�T�C�Y�͑傫���Ɣ��f����Ă���ꍇ������܂��D |
�����l�̊�͈͂ɂ������ȏ�P35����҂�Ώۂɑ��肵���f�[�^��95%�i�܂茒��҂ł����Ă�5%�͊O���j ���ϒl�̋�Ԑ���͕W���덷��p���邪�A������̏ꍇ�͕W�����B���z�Ɋւ��čl������K�v������B ���Q�l�� �u��͈́E�Տ����f�l�v�Տ������̃K�C�h���C�� JSLM2018�i���{�Տ�������w��j https://www.jslm.org/books/guideline/ |
�{���̉ۑ�i3,4�͔z�M�����A���P�[�g�j
1.�T�C�R����100��U�����Ƃ���o�ڂ̍��v��320�������D���ϒl��95%�M����Ԃ����߂�D�i��W�������߂�܂���ˁj2.P20�̐��f�[�^���ꕽ�ς�95%�M����Ԃ����߂�D
3.(�A���P�[�g)���ƃ��C�u�z�M�ɂ��ā@A:Teams�Ŏ��{���Ăق����@B:�c�C�L���X�Ŏ��{���Ăق����@C:�ǂ����Ŏ��{���Ă��ꏏ�ł�
4.(�A���P�[�g)�̃A���P�[�g�ɂ��Ă��ӌ������낵�����肢���܂��D
���ƌ�⑫
��5��@����̌���
���B�ڕW�T�|�P�m�����ǂ̂悤�ȈӖ������̂��̂���������
�T�|�Q��������̘_���\��������ł���
���ȏ�����P3-P7
���ȏ���O�́i01-02�jP46-51
���ȏ���\��Q3Q4�Q�lQ8�iP207,208,215,220�j
�m��
���鎖�ۂ��N���邱�Ƃ����҂����x�����i�����j���s�@�T�C�R����U���ĂR�̖ڂ��o��(y or n)
�m���@�T�C�R����U���ĂR�̖ڂ��o��(1/6)
�J��Ԃ����s���s���ƕp�x�����͂��̎��ۂ̊m�����������Ă���
������ΏۂƂ����ꍇ���s���J��Ԃ���H�������ȏꍇ���������������߂Â����J��Ԃ����ƌ���
�������߂��Ȃ��ƒP���ɔ�r�ł��Ȃ����i���ȏ�220�j
���s�̌��ʂ͎����Ő������B���Ƃ����Ă��ꂪ��ɐ������i�^�j�Ƃ͌���Ȃ�
���̎��s�ȍ~�ňقȂ錋�ʂ��ł�\����r���ł��Ȃ����i���Ɏ��s���J��Ԃ��Ȃ��ƂȂ炸�@�����o���Ȃ�
�i�̂ɈقȂ錻�ۂ̋N����m���ɂ�������臒l���߂āA�Ȃ��������Ƃɂ��Ĉ�ʐ����咣����X�^�C���j
���ۂ̋N����m�����������Ⴍ�Ă��A���ۂɋN����Ȃ��킯�ł͂Ȃ��B
�Q�l
�f�W�^���G�{�@�����ς̉J� �i�D�y���ݍ��Z�f�U�C���A�[�g�R�[�X�j
�~��܂ʼnJ�������̂Łu�J�������ΉJ���~��v�ƂȂ��Ă��܂�
�Q�l
�P��L��: �e�����`���i�j�R�j�R��S�ȁi���j�j
http://dic.nicovideo.jp/a/%E3%83%86%E3%83%AC%E6%9D%B1%E4%BC%9D%E8%AA%AC
�w���@�iP47�j
����̔ے�����肵�Ęb�������߂āA���̖������������ƂŖ��肪���藧�Ƃ���_�@���̂��邱�Ƃ��ؖ�����ɂ������āu�����������Ƃ��v���ؖ��ł��Ȃ����Ƃ������ɂ���
�i���i�Ⴂ�j���`����ɂ���Ԑ���Ŗ��炩�Ȃ悤�ɁC�m�����ł��l�͕ω�����j
�������D���̔��͌����@�ł͂Ȃ����S�Ƃ����l�����D
��������
���ȏ�P46-����O��݂����Ɍ��肷��̂ł͂Ȃ��A���肷�闝�R�E�m�M�����邩��m���߂�@�Ƃ���������
�菇�P�F���������Ă�i�A������H0����ёΗ�����H1�j
�w���@�Ɋ�Â��ؖ������Ă���B
�i�����Ȃ��������ؖ��ł��Ȃ��̂ŁA���̑Η��ł��鍷�����鉼�����̑�����j
�菇�Q�F���蓝�v�ʂ��v�Z����
���̎��ۂ̋N����m�����v�Z���Ă��邱�ƂɂȂ邪�A�p����m�����z�ɂ���Čv�Z�����قȂ�B
�i���f�[�^���m���̐��E�̃X�P�[���ɕϊ��j ���ȏ�P50�ł́i�R�j�̑O���̕���Z=�@�̕���������
�菇�R�F�L�Ӑ��������߂�
�m���I�ɕK�R�Ƌ��R��蕪���Ă���B��ʂɂT���ŕ����Ă��邪�P���̎�������
�菇�S�F�L�Ӑ����Ɣ�r���A���������p�̑�����
��j�A������H0�����p���Η�����H1�̑�
����
P49�̘b�͂�����
��������Б�����
P207�ꏏ�ȗL�Ӑ����Ŕ�r�����ꍇ�@�Б��͊��p�悪���݂��Ȃ����ƂƁC�����͊��p�悪�傫���Ȃ��Ă��܂��@���@�A�����������p����₷���Ȃ��
�L�Ӑ����͏��0.05�H
P208�L�Ӎ��͗L�Ӑ������ꏏ�ł�n=���傫���Ȃ�Ə��Ȃ����ł��D�ʂƔ��肳��Ă��܂��D
���G���[�@���G���[
���ȏ�P215����̉ߌ�
���G���[�̋N����m���i����ėL�Ӎ�������Ɣ���j���L�Ӑ���
�G���[���C�ɂ��Ȃ�����̓����A�s���̗ǂ����_�������邩������Ȃ��@���@�J�
�̂ɂ�݂����Ɍ��肷��̂ł͂Ȃ��A����܂ł̃X�g�[���[�����
����̉ߌ�i���G���[�j�E�E�E����Ĉꏏ�Ɣ��肷��m��
���G���[�̋N����m���i����ėL�Ӎ��������Ɣ���j�����o�ł��Ȃ����P�|���o�́iPower�j����
���o�́��P�|��
�T���v�������E�E�E���o�́��E�E�E����
��ʂɌ��o��0.8�`0.9�ňႢ�����ς�������ŃT���v���������肷��
���o�͂����オ��ƃ��G���[�̊m���͉����邪�C���v�I�L�Ӎ��ƗՏ��I�L�Ӎ��̘b���o�Ă���D
��������͗p�@����萳�����g���܂��傤
���B�x�m�F
�P�j��T�̉ۑ�P�̃T�C�R���̘b��100�s�����Ƃ���o�ڂ̑��a��385�������D�A������H0:�ʁ�3.5�@�Η�����H1:�ʁ�3.5�@�Ƃ��ā@�L�Ӑ���5%�����1%�Ō��肹���@�i�g�����T�C�R���͖{���̃T�C�R�����C�J�T�}�T�C�R�����j
���ƌ�⑫
��6��@�p�����g���b�N����
���B�ڕW�U�|�P�p�����g���b�N����̊拭��robustness������ł���
�U�|�Qt������s�����Ƃ��ł���
���ȏ�
��2��P44�@�v���ړx�Ɠ��v����������4��P57-69�@�֘A�Q�Q�̍��̌���
��5��P81-101�@�Ɨ��Q�Q�̍��̌���
��10��P204�@Q1�CQ2
�p�����g���b�N�ƃm���p�����g���b�N
���ȏ�P44���z�̌`��i�ꐔ�j�Ɉˑ����铝�v�ʁi���ϒl�@�W�����E�E�E�ʓI�ϗʁj
���z�̌`��i�ꐔ�j�Ɉˑ����Ȃ����v�ʁi���ʁ@�����l�@�p�[�Z���g�l�E�E�E���I�ϗʁj
���ȏ�P4-7,204
�p�����g���b�N����E�E�E�v���l�̕��z�����K���z�ł��邱�Ƃ�����
���K�m�����@�E�E�EQ-Q�v���b�g
�f�[�^���m���p�����g���b�N�Ƃ݂Ȃ��ď����ɒ����Ă�������p�[�Z���^�C�������߂āA�l���m�����z�i���K���z�j�ɑ�����Ċ��Ғl���Z�o���Ĕ�r����B
P11���G�Ȓ����f�[�^TG��p����
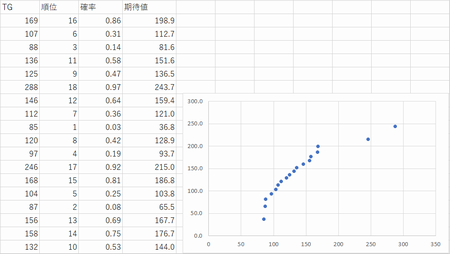
���Q�l�����K�m���v���b�g�̍����i���vWEB�@�Љ���T�[�r�X���v�����������j
https://software.ssri.co.jp/statweb2/tips/tips_8.html
�K�ȓ��v�����ɕK�v�ȍl����
P203-216Q2����@�ɂ���Ĕ��肪�قȂ�ꍇ
�@���f�[�^���o�Ă��猟��@��I������͓̂K�ł͂Ȃ�
Q5�L�Ӎ����肪���Ӗ��ȏꍇ
�@�����v�I�L�Ӎ��ƗՏ��I�L�Ӎ��̘b �@���ȏ��̌��ʗʂɑ���K�v�f�[�^�����ς��������̂��ȉ�
�@�e�Q10�f�[�^�Ō��肷���10kg���x�ƂȂ邪�A�����܂ő̏d���ω����Ă���ƂȂɂ��Ⴄ�o�������N�����Ă���C������
�@�e�Q1000�f�[�^���炢�Ō��肷���1kg���x�ŗL�ӂȌ��ʂƂȂ邪�A�{���ɈӖ�����̂��C�ɂȂ�
�@
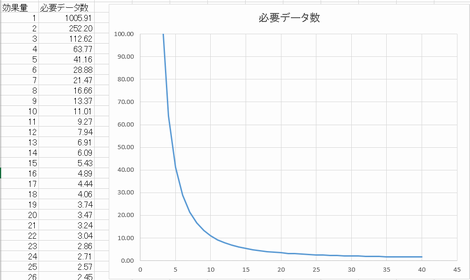
�@ �@���Q�l�����̎��Â͗Տ��I�ɗL�v���iPEDro�j
�@https://www.pedro.org.au/japanese/tutorial/is-the-therapy-clinically-useful/
�@���Q�l�����v�I�L�Ӑ���P�l�Ɋւ���ASA����
�@http://biometrics.gr.jp/news/all/ASA.pdf
�@�ȉ��������܂���
�@1. P�l�̓f�[�^�Ɠ���̓��v���f��������������x�����߂��w�W�̂ЂƂ�
�@2. P�l�́A���ׂĂ��鉼�����������m���𑪂���̂ł͂Ȃ�
�@3. �Ȋw�I�Ȍ��_�́AP�l������l�������ǂ����ɂ̂݊�Â��ׂ��ł͂Ȃ�
�@4. �K���Ȑ����̂��߂ɂ́A���ׂĂ���铧�������K�v
�@5. P�l�́A���ʂ̑傫���⌋�ʂ̏d�v�����Ӗ����Ȃ�
�@6. P�l�́A���ꂾ���ł͉����Ɋւ���G�r�f���X�̂悢�w�W�Ƃ͂Ȃ�Ȃ�
�E�f�[�^���傫���ꍇ�͋�Ԑ���̂ق����Ӗ�����B
���ȏ�P6�e�[�u���i�K�p�v���ɂ��g�������j
1�W�{t����E�E�E��2�W�{t����E�E�E�Q�Q�̓����U��
�̈Ӗ��́A�f�[�^���������Ƃ���Ȃ̂Ŗ��ɂȂ�Ȃ�
�Q�Q�̓����U���Ɋւ��ẮA�����O��Ƃ��Č��肪���藧���Ă���̂Łi�ȉ��ɏЉ��i�X�`���[�f���g�́jt�����
���_�A�����U�ł͂Ȃ��ꍇ�ɗp���錟��i�E�F���`��t����j������̂ł����A��������ŏ�����g���������ǂ��Ƃ����b������܂��B
�m���p�����p�����g���b�N�̘b�Ɠ��l�ł����A�ǂ���ł�낤�Ƃ��L�Ӎ����o�Ă邮�炢���m�Ȃ��̂����z�ł͂���܂���
2�Q�̍��̌���
1�W�{t����i�֘A�Q�Q�j
���ȏ�P58P60���8�����Ȃ���
�֘A����Q�Q�i�y�A�j�E�E�E��̌Q���Q�肵�Ă���
�O��̍�������
t�l�i�W�������ꂽ���蓝�v�ʁj�E�E�E�Q�Q�̃y�A�̍��̕��ς�W���덷�Ő��K����������
�A�������͑O��̍����[��
���蓝�v�ʂƗL�Ӑ�������t�l���r����B
2�W�{t����i�Ɨ��Q�Q�j
���ȏ�P82�`�@P84���12�@P87���13������̏ꍇ�́A���ȏ��I�ɂ�F����iP86)�œ����U���m�F���Ă���̎菇�ɂȂ�B
��W�{�Ƃ̈Ⴂ�͕��U���Q�킠�邱�Ɓi��W�{�̓y�A�̍����Ƃ�̂ň�j
���̂��ߍ�������
t�l�E�E�E���ꂼ��̌Q�̕��ς̍���W���덷�Ő��K����������
F���z�E�E�E���Q���z�̎��ɂ��b�����܂�
�@
���B�x�m�F
�P�jP76���10��t����Łi�L�Ӑ���5%�y��1%�Łj�j �Q�jP60���8�𖬔��i�O�j��^�Q�i6�l�j�C�����i��j�𓊗^�Q�i6�l�j�ƕʁX�̔팱�҂̑���l�Ƃ����ꍇA�܂Ɍ��ʂ�����Ƃ����邩���肹��D�i�L�Ӑ���5%�����1%�Łj�����U�i2�Q�̕��U���قȂ�Ƃ͌����Ȃ��j�Ƃ���D
�⑫
|
���o�X�g�l�X�Ƃ͉����H�iHM's webpage�j https://tenure5.vbl.okayama-u.ac.jp/~hisaom/HMwiki/index.php?%E3%83%AD%E3%83%90%E3%82%B9%E3%83%88%E3 %83%8D%E3%82%B9%E3%81%A8%E3%81%AF%E3%81%AA%E3%81%AB%E3%81%8B%EF%BC%9F |
��7��@�m���p�����g���b�N����
���B�ڕW�V�|�P�p�����g���b�N����ƃm���p�����g���b�N����̈Ⴂ������ł���
�V�|�Q�m���p�����g���b�N������s�����肷�邱�Ƃ��o����
��W�{Wilcoxon����
�E�B���R�N�\���̕����t���ʘa�������ȏ��iP6)�E�E�E���z�^�C�v���ړx�C���U�̐���Ȃ�
���ȏ��iP74�j
�P�F�y�A�̃f�[�^�̍�d�����߂�
�Q�Fd�̐�Βl��肻�ꂼ��̍��id�j�̏��ʁi�����j�����߂�
�@�@�����ʂ̘b�E�E�E���ȏ�P76�Q��
�R�F���蓝�v��T�́{�C�|�ʂɏ��ʂ𑫂������̂ŏ�������
T0=min(T1,T2)
�L�ӊm���ɂ��Ă͒��ڌv�Z�o���邪�iP75�j���X�ƌv�Z���Ă����̂͑��
n��25�܂ł�Wilcoxon����\���g���Ă��������iP274)
N�������Ȃ��Ɓi�̕����j����ۗ��ɂ����Ȃ�Ȃ�
���ȏ�P78�Q�Ƃ̂���
n��25�͐��K���z�ɋߎ��ƌ��Ȃ���z�l�����߂���@�Ō���
���ϒl
���蓝�v��T�̕��ϒlT1=n(n+1)/2-T2
T2=n(n+1)/2-T1
(��k=n(n+1)/2)
T1+T2=n(n+1)-T1-T2
2*(T1+T2)=n(n+1)
��T=(T1+T2)/2=n(n+1)/4
�W���덷
��T=��(n(n+1)(2n+1)/24)���蓝�v��
Z=(T-��T)/��T�A���
P137�Q��P76(���10)�Ő������܂��D
Mann-Whitney����
��W�{�ɂȂ�Ƃ�₱�����Ȃ�̂̓p�����g���b�N����Ɠ���P102-113�Q��
���蓝�v��
���Q�̌X�ɂ��āA����������Q�ő傫���̐��̑��a�����߂Č��蓝�v�ʂƂ��Ă���
�P�F����Q�iA�j�̒l���ꂼ�ꂪ��������̌Q�iB�j�ɓ������Ƃ����Ƃ��ɁiA�́j���̒l�����iB�̌Q�̂Ȃ��Łj�l���傫�������J�E���g����B�iA�Q�́j�S�Ăɂ��čs���a���Ƃ�B�i����-1�̘b�j
�Q�FA��B�����ւ��ĂP�F�Ɠ��l�̌v�Z�����邩�A������B�Q�̘a�����ߏ������������蓝�v��U�Ƃ���
�@�@�����ʂ̘b�E�E�E���ȏ�P103�Q��
��������W�{���������Ȃ�Ɛ��K���z�̘b���o�Ă���
���ϒl
��U=n1n2/2�W���덷
��U=��n1n2(n1+n2+1)/12)���蓝�v��
Z=(U-��U)/��U���B�x�m�F
�V�|�P�jP63���K�R�ɂ��ăm���p�����g���b�N������s���A�p�����g���b�N����̌��ʂƔ�r����B�V�|�Q�jP86���P�T�ɂ��ăm���p�����g���b�N������s���A�p�����g���b�N����̌��ʂƔ�r����B
���ƌ�⑫
�{���̗]�k |
��8��@�v���l�f�[�^�̌���
���B�ڕW�W�|�P���z�Ɛ��K���z�̊W������ł���
�W�|�Q�J�C��敪�z�Ɛ��K���z�̊W������ł���
���ȏ���7��P125-151
�v�ʒl�ƌv���l
�v�ʒl�E�E�E�ʂ𑪒��v���l�E�E�E�p�x�𑪒�i���`�ړx�j
�ʓI�ϗʂ͕p�x�̑�����o����
�ǂ̂悤�ȃf�[�^�ɂ��g����̂ŁC�F�X�ȂƂ���ŏo�Ă���
���z�i���Z�ŏK���Ă܂���ˁj
�W�{�̑傫��=n���ۂ̋N����m��=p
r=�o���x��
np=n�s���J��Ԃ����Ƃ��Ɏ��ۂ̋N����i���ғx���j
���Q�Q�iP128)�ŏq�ׂĂ��锭�����͊��ԗL�a���i�܂芄���j�̂��ƁD
|
��Ɨ��Ɗ����̈Ⴂ�ɂ��� ��E�E�E�قȂ���̂��r�i���P�ʂɂȂ�ꍇ�����邪�j ���E�E�E�䂾�����ԂƔ�r�i�P�ʂ�/sec�@/min�@/hr�@�ƂȂ�j �����E�E�S�̂ƈꕔ�i�������́j���r�i���P�ʁj �ȉ��Q�l�ɂ��Ă������� ��13��@��Ó��v�i�U�j�|��Ɨ��Ɗ����i���ی���Ñ�w�@��Ï��w�Q�O�P�U�j http://www.medbb.net/education/ohsumedinfo2016/#13 |
�{���̗]�k |
��9��@�Ɨ����Q�Ԃ̔�r
���B�ڕW�X�|�PF���z�ƃJ�C��敪�z�̊W������ł���
�X�|�Q���U���͂Ƒ��d����̈Ⴂ������ł���
���ȏ�
��5��P94-97
��8��P153-172
��10��P217-219
F���z
�J�C��敪�z�Ɠ��������U�Ɋւ���m�����z���ꂼ��̌Q�̃J�C���l�̔䁁���U�̔�E�E�E�e�l�i�e�̓t�B�b�V���[�̂e�j
F���z�ƃJ�C��敪�z�̊W
��^2(��)=�ˁ~F�i��,���j
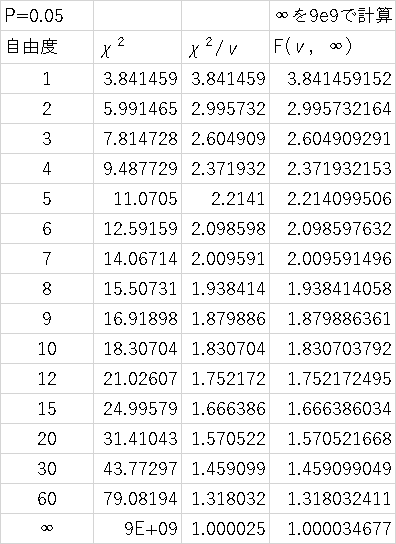
�����U�̌���iF����j�iP94�j
�����U���̌���E�E�E���U������߂�F�l��蔻���u2�Q�̕��U�͈قȂ�Ƃ͌����Ȃ��v�E�E�E�A�����������p�ł��Ȃ��i�ۗ��j
�@
������r
�S�Q���ꊇ���Ĕ�r�ꌳ�z�u���U���́iP155�j
3�ȏ�̕W�{�@�Q�ԕ��U�ƌQ�����U�̕��U���Q�ԕ��U�E�E�E�Q�ʂ̕��ςƌQ�ʂ̕��ς̕��ςŋ��߂�D���R�x�͌Q��k-1
�Q�����U�E�E�E���ꂼ��̒l�ɑ��đ�����Q�̕��ς��g���ċ��߂�D���R�x�͑��W�{��n-�Q��k
�Q�ԕ��U�ƌQ�����U�̔���Ƃ�
Kruskal-Wallis����
���ȏ�P164P166���33�̃f�[�^�ŋɒ[�l�̘b
������r���č������������瑽�d��r����Ƃ����̂́A�����q�ׂ������ɂ�邪�E�E�E����@�I�ɂ��̂悤�ɕ��͂���P�[�X�͑��X
���d����
���ȏ�P217�|�C���g�Ƃ��ẮA���ꂼ��̌��肪�Ɨ����������ɂ��ƂÂ������̂ƍl���ėǂ����ۂ��B�ǂ��̂ł���Α��d����ɂȂ�Ȃ�
��A�̂��̂ł���ΑΗ��������l�����Ƃ��ɗL�Ӑ������T���ƌ����Ȃ���T���ɂȂ��Ă��Ȃ��̂ł́H
���d�Ɍ��肷�邱�Ƃłǂꂩ������A�������͊��p�ł���̂ŗႦ��3�Q�������肾�ƗL�Ӑ���0.05�ő��d����i6�ʂ�j����ƗL�Ӑ�����0.265�ɂȂ��Ă��܂��B�i����悭�Ȃ��j
�L�ӊm����@
Bonferrini�̏ꍇ��6�ʂ茟�肷��̂ł���A�ꌟ�肠����̗L�Ӑ�������0.05/6=0.0083�ƂȂ�B�S�̂ł�1-(1-0.00833)^6=1-0.95103=0.0490Sidak��̏ꍇ�͓��l��1-(1-0.05)^(1/6)=0.008512�@1-(1-0.008512)^6=1-0.95=0.0500
���Q�ɂȂ�قnj��肠����̗L�Ӑ����������遨�����o�ɂ���
���d��r�@
�p�����g���b�N�@Tukey�@�E�E�E�e�y�A�ɑ��镽�ϒl�̍��̌���
Dunnett����E�E�E��̑ΏیQ�Ƃ̑Δ�
�m���p�����g���b�N�@
Dunn�@
���B�x�m�F
�X�|�P�j158���31�ɂ���Kruskall-Wallis�����p���Ĕ��肹���X�|�Q�j����זE�����x�����ɂ��4�Q�ɂ킯�Ĕ|�{���s���f�[�^�𑪒肵���D�W�{���́CA=4,B=3,C=5,D=8�ł������D�Q�Ԃ̕������aSA��60�@�Q���̕������aSE��40�������ꍇ�ꌳ�z�u���U���́@�L�Ӑ���5%�Ō��肹��
�X�|�R�j�j���ʂɌ����̊Ǘ��p�����𑪒肵���B���ꂼ�ꑍ������œ�W�{t������s�����B�L�ӊm����Bonferroni��@��p���ėL�Ӑ����T���Ŕ��肵�L�ӂȑg�ݍ��킹�����ׂċL��
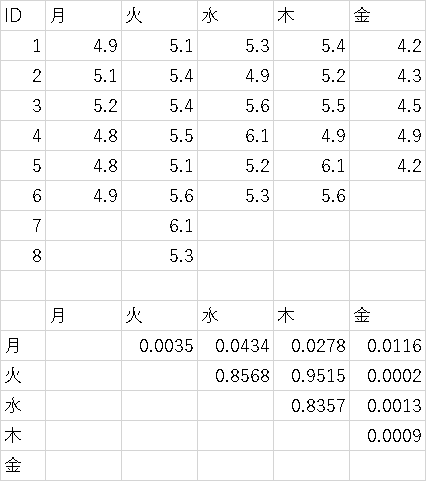
�⑫
�����̗]�k
��10��@���W���E��A����
���B�ڕW�P�O�|�P���W��������E�v�Z���邱�Ƃ��o����
�P�O�|�Q��A�������ǂ̂悤�Ȃ��̂������E�v�Z���邱�Ƃ��o����
����
�i���ȏ�P174�j correlative���֊W������E�E�E�֘A������
���֊W�������E�E�E�֘A���Ȃ�
�����̉e�����邩�Ȃ���
����
cause and effect�����ƌ���
���ʊW������E�E�E�e��������
���ʊW�������E�E�E�e�����Ȃ�
�֘A������i���ւ�����j���e�����y�ڂ��W�i���ʊW������j�ƍl����i�l�������Ȃ�j
��
�������z���|�x����E�E�E�E���֊W��
�^�o�R���z���l�ɃR�[�q�[�����ސl�������̂́E�E�E�iyahoo�m�b�܁j
http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1293675642
���̊W���g����
�R�[�q�[�����ށ|�x����E�E�E���֊W��
�ł��R�[�q�[���x����̌����Ƃ͂�����Ȃ�
�R�[�q�[�����҂ɔx���������R�́H�����K���Ƃ̊֘A������
�A�����J�Ŗ�50���l��Ώۂɂ�����������
from International journal of epidemiology
http://medley.life/news/item/5589521b660815fe00d5ec8e
�R�[�q�[�Ɣx����̑��֊W�Ɋ��荞��ł���i�ǂ���Ƃ����֊W������j��ԁ���)
���荞��ł��邻�ꁁ�𗍈��q�E�E�E����
�R�[�q�[�Ɣx����Ɉ��ʊW�������Ƃ����Ȃ炻�̊W�͋^������
�{���Ɓi���v�w�j�͈�Ìn�ΏۂŁu�����Â��y�ڂ��e���₻�̗v���Ɋւ���@�����������������@��T������w�╪��v
�i��ナ�n�r���e�[�V�������w�Z�@���v�w�Q�O�P�T�i���w�Ö@�w�ȁj���j
�m�肽���̂́u�e���v�ł��邩��ړI��������Ȃ��悤��
���}
X����Y���Ɉ�̑Ώۂɗ^�����邻�ꂼ��̒l���v���b�g�i��F�g���Ƒ̏d�j�Ƃ肠�����}�ɂ���ƊW�������I�ɂ킩��i�ꍇ�����遨�𗍌��ی��ݍ�p�ɒ��Ӂj
���W��
-1����1�܂ł̒l���Ƃ�i���ȏ�P174�j�{�̏ꍇ���̑��ց@�|�̏ꍇ���̑���
X�����������Y����������E�E�E1
X�����������Y�͌�������E�E�E-1
X���������悤���������悤��Y�͊W�Ȃ��E�E�E0
���W����0�o�Ȃ���Α��ւ́u����v���P�������x�͐�����0���痣���قNj����Ȃ�
��ʂɁ`0.2�ł���Α��ւ͂Ȃ��A0.7�`�ł���������ւ̖ڈ��Ƃ���Ă�B
�i���̋��ȏ���r�\�����Ă��܂��D���ւ̋����ɂ���Č���̌��ʂ����܂邯�ǁCn�̐��ɂ��@P278�\�W�j
X���Ō����Ƃ��̃o���c�L���Y���Ō����Ƃ��̃o���c�L������Ɍv�Z���Ă�
�o���c�L���U�z�x�E�E�E���U�E�E�E���̓��̕���
�����U������Ώۂ�X���̕���Y���̕����悶�����̂��x�[�X
����
��{�����̂Ƃ���͕������a�̘b�ɂȂ��Ă��邪�W�{���U�̏ꍇ���ӂ�n�Ŋ���Ȃ��Ƃ����Ȃ�
����ƁE�E�E���̕��ρ|���ς̓��@�Ƃ������Y�����̂���������o����
�@�@
| X�̕� | Y�̕� | �悶������ |
|---|---|---|
| �{ | �{ | �{ |
| �{ | �| | �| |
| �| | �{ | �| |
| �| | �| | �{ |
�����U��X��Y���̃o���c�L����������Ă���̂ł��̂܂܂̐������Ɖ��߂��ɂ�����X��Y�̕W�����ŏ�����i���K���j�����W��
�����Ŗ����ꍇ�͕ϊ��i�Ⴆ�Αΐ��ϊ��j���Ă���v�Z���Ă��悢�i�ΐ��O���t�j
�ΐ��O���t�̗�i���ᎆ�l�b�g�j
http://houganshi.net/taisuu.php
��A����
X���̒l��Y���̒l�𐔎��iy=ax+b�j�Ŏ����������������Ƃ��ɂ��ꂼ��̓_����̍��i�c���j��2�悵�đ��������́i�����a�j���ł����������̐�������A����
����W��
���W�����悷��Ƌ��߂��������ɂ���Đ����ł��銄���������B�i��^���Ƃ��j
�܂荂��������قǐ����Ő����o���邱�ƂɂȂ�
���B�x�m�F
�v���lX,Y�̊W�ׂ�Ɖ��\�̂悤�ɂȂ����P�O�|�P�j��A����y=a+bx�����߂�
�P�O�|�Q�j���W��r�����߂�
�P�O�|�R�j�L�Ӑ����T������тP���ő��ւ����邩���肹��
| ID | �v���l�� | �v���l�� | ���Q | ���Q | ���� |
|---|---|---|---|---|---|
| 1 | 2 | 50 | |||
| 2 | 2 | 40 | |||
| 3 | 2 | 30 | |||
| 4 | 4 | 60 | |||
| 5 | 2 | 20 | |||
| 6 | 4 | 50 | |||
| 7 | 8 | 50 | |||
| 8 | 8 | 60 | |||
| 9 | 8 | 70 | |||
| 10 | 10 | 70 | |||
| ���v | 50 | 500 |
���ƌ�⑫
�{���̗]�k |
��11��@���ϗʉ��
���B�ڕW�P�P�|�P���ϗʉ�͂̕K�v���ɂ��Đ����ł���
�P�P�|�Q�d��A���͂ɂ����Ăǂ̂悤�ɕϐ����I��Ă��邩�����ł���
���ϗʉ�͂ɂ���
���ȏ�P5�����̕ϗʂ�p���āE�E�E�T���I
�\���E�E�E�i�d��A���́j
�v���E�E�E�O�I����Ȃ��i�听�����́j
�u�W���肻���ȃf�[�^���W�߂����ǂǂ�������܂Ƃ܂�̂��v�Ƃ����Y�݂��������Ă����Ƃ����������₷��
�d��A����
���ȏ�P223�i��A�����̘b���v���o�����P��A���́j
��A�E�E�E���ɖ߂�E�E�E���炩�i�藝��W�j�Ɋ�Â��߂��Ă���
�P��A����
���ȏ�P195��A�W���E�E�EY=a+bX��b
����W���i�ȑO�̎��ƎQ�Ɓj
�d��A����
Y=a+b1X1+b2x2+�E�E�E �ړI�ϐ��E�E�EY�����ϐ��E�E�EXi
�Ή�A�W���E�E�Ebi
�W���Ή�A�W���@��*�@�ړI�ϐ��Ɛ����ϐ��̊W��W���������Ƃ��̕Ή�A�W���E�E�E
�ړI�ϐ��͗ʓI
�����ϐ��͗ʓI�ł����I�i0,1�j�ł�
�P��A�Ɠ������ŏ����@�ŋ��߂�
����W���E�E�E�����ϐ��𑝂₷�ƒl�͏㏸ ���R�x�����ς���W���E�E�E1-(1-R2)(n-1�j/�in-k-1�j n=�W�{���@k=�Ɨ��ϐ�
VIF�@���U�g��v��
���d��������������w�W
���d�������E�E�E�Ɨ��ϐ������̓Ɨ��ϐ��Ƒ��ւ�����E�E�E�Ή�A�W���̕W���덷����
VIF=(1-Ri2)-1
Ri2�F���̓Ɨ��ϐ��ŏd��A�������Ƃ��̌���W��
�ڈ��Ƃ��Ă�10�ȉ��ł�����̂܂�
�ȉ���SPSS�̏o�́i�f�[�^�͋��ȏ�P11�́u���G�Ȓ����f�[�^�v�j��BMI���]���ϐ��@����ȊO�iID�@���ʏ����j��Ɨ��ϐ��Ƃ����ꍇ
�ϐ������@��
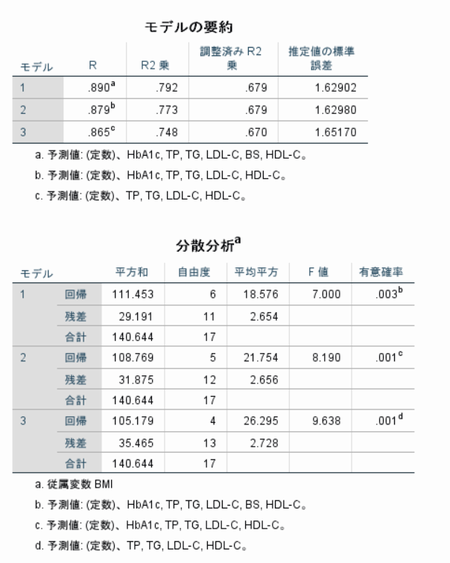
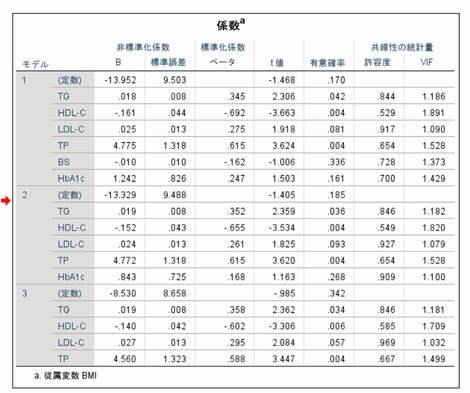
�G�N�Z���̏ꍇ(2013)
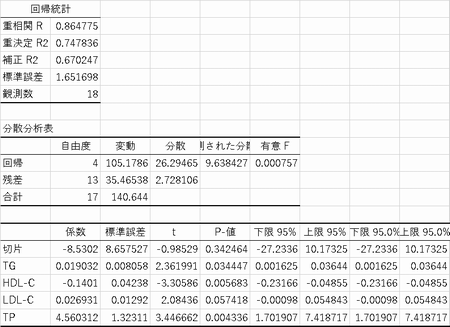
���B�x�m�F
�P�j���Ǝ����Ɏ������f�[�^���d��A���͂ɂ�蓾��ꂽ��������BMI�l�𐄒肹����12��@���Ί댯�x
���B�ڕW�P�Q�|�P���Ί댯�x�������w�W�ɂǂ̂悤�Ȃ��̂����邩�����ł���@
�P�Q�|�Q�Ǘ�Ώƌ����ł͑��Ί댯���I�b�Y��ŎZ�o���闝�R������ł���
���̎��Ƃł͑��Ί댯�x=Relative Risk �͈�ʓI�ȗp��ł���A���̎Z�o�w�W�̈�ɑ��Ί댯�����X�N��iRisk Ratio�j������Ɛ������܂�
��ʓI�ɂ͂�����ւ�̌��t�S�`���S�`���ł��B
�ώ@����(Observational study)
���f�����iCross-sectional study�j���I�Ǝ������ɕ]��
���Ԏ����Ȃ��ꍇ�������i��O�͐��ʂȂǁj���ʊW�܂ł͕s���ɂȂ��Ă��܂��₷��
�R�z�[�g�����iCohort study�j
�Ώۂɔ��I���Ă���l�X�ƔI�Q��ݒ�A�ǐՒ������Ă����X�^�C��
�ʏ�O���������A�������ɂ݂��ړI�R�z�[�g�����Ƃ����̂�����B�i��X�ł����I�Q�Ɋւ�������ꍇ�j
�Ǘ�Ώƌ����iCase-control study�j
�����ԁi�Ⴆ�Εa�C�ɜ늳���Ă���j�Q�ƁA�늳���Ă��Ȃ��Q��ݒ�A���Ԃ�k���Ē������Ă����X�^�C��
�������ɂ����s���Ȃ��i�O�������Ɣ��I�������̏������������Ȃ�j
�����I�����i��������j�iintervention study�j
�R�z�[�g�����̏ꍇ�A���I�Q�i����Q�j�������҂�����t����@���@�팱�҂ɑ���ϗ��I�z�����̗v����ׂɊ���t���邱�Ƃ��o����ꍇ�͌𗍈��q�𐧌�ł���i���Ƃ����҂����j
�ϗ��I�ɍl����Ɣ����Q�̕����s���v�ɂȂ��Ă��܂��\���������̂ŁA�z�����������f�U�C�������߂���
�����p�f�[�^
| ���a���� | ���a�� | �v | |
|---|---|---|---|
| ���I�L | A | B | A+B |
| ���I�� | C | D | C+D |
| �v | A+C | B+D |
���Ί댯
Risk Ratio(RR)�u���X�N��v�ƌ����������킩��悢�i�Ǝv�����j
���I�i����j�̗L�鎞�Ɩ��̎��̊댯�������w�W�̔�
�댯�������w�W�ɂ͜늳�����L�a����玀�S�����
A�`D:���a�����p�x�i�p�x�ȊO�ɜ늳�����L�a���E�E�E�j
���I�L�Q�̔��ǃ��X�N��A/(A+B)
���I���Q�̔��ǃ��X�N��C/(C+D)
���X�N�䁁A/(A+B)�^C/(C+D)
�����A�����p�x���Ⴏ���A+B��B�@C+D��D
�@���X�N���A/B�^C/D��AD/BC
�I�b�Y��
Odds Ratio(OR)�댯�Ȏ��ۂ��N�����ꍇ�ƋN���Ȃ������ꍇ�̎w�W�̔�i���I�b�Y�j�ɂ��Ĕ��I�i����j�̗L�����ɋ��ߔ���Ƃ�������
���ǗL�Q�̔��I�I�b�Y��A/C
���ǖ��Q�̔��I�I�b�Y��B/D
�I�b�Y�䁁A/C�^B/D
�@�@�@�@��AD/BC
��L�̂悤�ɔ��Ǖp�x���Ⴏ��I�b�Y��ƃ��X�N��̋ߎ��l�ƂȂ�
���B�x�m�F
�P�j���Ί댯�x���Z�o�����R�z�[�g����
| �s�������� | �s�����Ȃ� | �v | |
|---|---|---|---|
| ���I�Q | 100 | 1900 | 2000 |
| �I�Q | 50 | 1950 | 2000 |
| �v | 150 | 3850 | 4000 |
| �s�������� | �s�������� | �v | |
|---|---|---|---|
| ���I������ | 50 | 30 | 80 |
| ���I�� | 50 | 70 | 120 |
| �v | 100 | 100 |
���ƌ�⑫
|
�\�I�ƌ��ʂ̊W�͂킩�邪�C����܂ł̌o�߂͂ǂ�����́H���������ԕ��� |
��13��@���x�E���ٓx�EROC�Ȑ�
���B�ڕW�P�R�|�P���ʓ����l�̌v�Z���o����
�P�R�|�Q�]�����ʂ��ROC�Ȑ����쐬���]����J�b�g�I�t�l�̌������o����
�����@�̐f�f�I�L�p����]������b
�L�a���̉e������w�W�A�Ȃ��w�W�����Ă�������
�u���v�ł͂��邪���ۂɂ͊����B���_�L�a���Ƃ������i���ԗL�a���͎��_�L�a���Ɋ��Ԓ��̜늳�����������́j
�i��8��Ŕ�E���E�����̘b�����܂������j
���x�Ɠ��ٓx
���ȏ��iP116�j���x��P(�z��|�c) �@�����Q�ɂ�����^�z���̊���
�U�z������P(�z��|�cc) ���Q�ɂ�����U�z���̊���
���ٓx���P�|�U�z���� ���Q�ɂ�����^�A���̊���
�\���l
�L�a���̉e������
�@�z���I������P(�c|�z��)
�@�A���I������P(�cc|�A��)
�����@�̕]���w�W
�@�ޓx�䁁���x/�U�z�����@
�@�I�b�Y�䁁���ȏ��Q�Ɓ@�����̗L�p��
�@AUC��ROC�Ȑ���`���ĎZ�o�@�����̕��ʔ\
���ł��z���Ɣ��f���錟���͊��x���U�z�������P�ɂȂ�
�i�Ȃ�ł�����ł��A����܂�!�I�@�̃m���j
ROC�Ȑ�
���ȏ��iP119�j���ʓx�̕���
���x�ƋU�z�����i�P�|���ٓx�j��p���ċȐ���`��
���21�ŇE���J�b�g�I�t�l�Ƃ����Ƃ��̗z���I������7/9�@�A���I����=8/11
���B�x�m�F
�P�R�|�P�j2��ނ̌����@A,B���{�s�����Ƃ���ȉ��̌��ʂ��D
AUC�����߂ǂ���̌������D��Ă��邩�]������
�Ȃ��J�b�g�I�t�l��12.0~15.5�܂�0.5���݂Őݒ肵�]���̂���
A�@
| �����Q | 14.3 | 15.2 | 13.8 | 14.1 | 13.9 | 12.6 | 14.2 | 14.6 | 13.1 | 13.7 |
| ���Q | 13.2 | 14.1 | 13.8 | 13.6 | 12.9 | 12.4 | 12.1 | 12.3 | 12.3 | 12.8 |
| �����Q | 14.3 | 15.2 | 13.8 | 14.1 | 13.9 | 12.6 | 14.2 | 14.6 | 13.1 | 13.7 |
| ���Q | 13.2 | 14.3 | 13.8 | 12.9 | 14.4 | 14.4 | 12.1 | 15.3 | 12.3 | 12.8 |
���ƌ�⑫
�{���̗]�k |
��14��@�������ԕ���
���B�ڕW�P�S�|�P�J�v�����}�C���[�@�ɂ�鐶���Ȑ��̍쐬���o����
�P�S�|�Q���O�����N����ɂ�鐶�����̍��̌�����s�����Ƃ��o����
�������ԕ��͎͂��Ö@���̕]���Ɏ��Ԏ����܂߂�����
�C�x���g�����܂ł̎��Ԃɂ�镪��
������
�������ɂ͌v�Z�����������d�Z�@�̕��y�ɂ��Kaplan-Meier�@�ł��e�ՂɌv�Z�o���鎞��
�����������͔�̓���Ȍ`�ԂŒP�ʎ��Ԃ�����̃C�x���g����\�킷
�i��12��̎��ƂŔ䗦�������グ�܂����j
Kaplan-Meier�ŋ��߂��C�x���g�����i�����j����1-�C�x���g�����i���S�j���́A���ł͖������_�C�x���g�i���S�j�����Ȃ̂Œ���
���Q�l��
���҂̐������i�n�悪��o�^�S�����c��j
http://www.jacr.info/about/survival.html
���ږ@�͊����B���r�ł��肪����ƍ���
�����ی������@�������B���r�ł���ɂ��Ă͂P�^�Q���ώ@���ԂɊ܂߂Ă��邪�C�x���g�����i���S�j�҂̊ώ@���Ԃ��l�����Ă��Ȃ��̂ŗ��ł͖����i�l�����Ă�����l�N������i���j�ɂȂ�j
�J�v�����}�C���[�@�ɂ��C�x���g�������̌v�Z
�[�f�[�^| ����ID | �f�f�� | �ώ@�I������ | ����ID | �f�f�� | �ώ@�I������ | ����ID | �f�f�� | �ώ@�I������ | ����ID | �f�f�� | �ώ@�I������ | ����ID | �f�f�� | �ώ@�I������ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | b | 3 | 11 | a | 8 | 21 | b | 9 | 31 | b | 24+ | 41 | a | 3+ |
| 2 | b | 5 | 12 | b | 14 | 22 | b | 18 | 32 | a | 12 | 42 | b | 8 |
| 3 | b | 6 | 13 | b | 9 | 23 | a | 12+ | 33 | a | 3+ | 43 | b | 24+ |
| 4 | b | 14 | 14 | a | 1 | 24 | a | 3 | 34 | b | 13 | 44 | a | 5+ |
| 5 | a | 7+ | 15 | a | 2 | 25 | b | 17+ | 35 | b | 17 | 45 | b | 14 |
| 6 | a | 14 | 16 | a | 3 | 26 | a | 7 | 36 | a | 3 | |||
| 7 | a | 17 | 17 | a | 13 | 27 | a | 8 | 37 | b | 15 | |||
| 8 | b | 21 | 18 | b | 21 | 28 | a | 12 | 38 | b | 13 | |||
| 9 | b | 21 | 19 | b | 16 | 29 | b | 12+ | 39 | a | 21 | |||
| 10 | b | 16 | 20 | b | 24+ | 30 | a | 1 | 40 | b | 18 |
�������̌v�Z
����a| �f�f����̌��� | ���J�n���̐����� | ���S�� | ���r�ł��萔 | ���S���� | �������� | �ݐϐ����� |
|---|---|---|---|---|---|---|
| 1 | 20 | 2 | 0 | 0.100 | 0.900 | 0.900 |
| 2 | 18 | 1 | 0 | 0.056 | 0.944 | 0.850 |
| 3 | 17 | 3 | 2 | 0.176 | 0.824 | 0.700 |
| 5 | 12 | 0 | 1 | 0.700 | ||
| 7 | 11 | 1 | 1 | 0.091 | 0.909 | 0.636 |
| 8 | 9 | 2 | 0 | 0.222 | 0.778 | 0.495 |
| 12 | 7 | 2 | 1 | 0.286 | 0.714 | 0.354 |
| 13 | 4 | 1 | 0 | 0.250 | 0.750 | 0.265 |
| 14 | 3 | 1 | 0 | 0.333 | 0.667 | 0.177 |
| 17 | 2 | 1 | 0 | 0.500 | 0.500 | 0.088 |
| 21 | 1 | 1 | 0 | 1.000 | 0.000 | 0.000 |
| �f�f����̌��� | ���J�n���̐����� | ���S�� | ���r�ł��萔 | ���S���� | �������� | �ݐϐ����� |
|---|---|---|---|---|---|---|
| 3 | 25 | 1 | 0 | 0.040 | 0.960 | 0.960 |
| 5 | 24 | 1 | 0 | 0.042 | 0.958 | 0.920 |
| 6 | 23 | 1 | 0 | 0.043 | 0.957 | 0.880 |
| 8 | 22 | 1 | 0 | 0.045 | 0.955 | 0.840 |
| 9 | 21 | 2 | 0 | 0.095 | 0.905 | 0.760 |
| 12 | 19 | 0 | 1 | 0.760 | ||
| 13 | 18 | 2 | 0 | 0.111 | 0.889 | 0.676 |
| 14 | 16 | 3 | 0 | 0.188 | 0.813 | 0.549 |
| 15 | 13 | 1 | 0 | 0.077 | 0.923 | 0.507 |
| 16 | 12 | 2 | 0 | 0.167 | 0.833 | 0.422 |
| 17 | 10 | 1 | 1 | 0.100 | 0.900 | 0.380 |
| 18 | 8 | 2 | 0 | 0.250 | 0.750 | 0.285 |
| 21 | 6 | 3 | 0 | 0.500 | 0.500 | 0.143 |
| 24 | 3 | 0 | 3 | 0.143 |
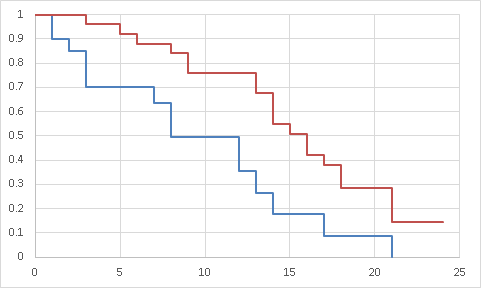
����a�F��
����b�F�Ԑ�
���O�����N����
�J�C��敪�z�ɂ�錟����s���i���ғx���Ɣ�r���ăo���c�L�����邩�ۂ��j
�C�x���g�������̃N���X�\�i�J�b�R���͊��ғx���j
�P����| ���S�� | ������ | ���v | |
| �Ǘ�a | 2(0.889) | 18(19.111) | 20 |
| �Ǘ�b | 0(1.111) | 25(24.889) | 25 |
| ���v | 2 | 43 | 45 |
| ���S�� | ������ | ���v | |
| �Ǘ�a | 1(0.419) | 17(16.581) | 18 |
| �Ǘ�b | 0(0.581) | 25(24.419) | 25 |
| ���v | 1 | 42 | 43 |
�ώ@�x���y�ъ��ғx��
| �f�f����̌��� | a�ώ@�x�� | a�ł��萔 | a���l�� | a���ғx�� | b�ώ@�x�� | b�ł��萔 | b���l�� | b���ғx�� |
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 0 | 20 | 0.889 | 0 | 0 | 25 | 1.111 |
| 2 | 1 | 0 | 18 | 0.419 | 0 | 0 | 25 | 0.581 |
| 3 | 3 | 2 | 17 | 1.619 | 1 | 0 | 25 | 2.381 |
| 5 | 0 | 1 | 12 | 0.333 | 1 | 0 | 24 | 0.667 |
| 6 | 0 | 0 | 11 | 0.324 | 1 | 0 | 23 | 0.676 |
| 7 | 1 | 1 | 11 | 0.333 | 0 | 0 | 22 | 0.667 |
| 8 | 2 | 0 | 9 | 0.871 | 1 | 0 | 22 | 2.129 |
| 9 | 0 | 0 | 7 | 0.500 | 2 | 0 | 21 | 1.500 |
| 12 | 2 | 1 | 7 | 0.538 | 0 | 1 | 19 | 1.462 |
| 13 | 1 | 0 | 4 | 0.545 | 2 | 0 | 18 | 2.455 |
| 14 | 1 | 0 | 3 | 0.632 | 3 | 0 | 16 | 3.368 |
| 15 | 0 | 0 | 2 | 0.133 | 1 | 0 | 13 | 0.867 |
| 16 | 0 | 0 | 2 | 0.286 | 2 | 0 | 12 | 1.714 |
| 17 | 1 | 0 | 2 | 0.333 | 1 | 1 | 10 | 1.667 |
| 18 | 0 | 0 | 1 | 0.222 | 2 | 0 | 8 | 1.778 |
| 21 | 1 | 0 | 1 | 0.571 | 3 | 0 | 6 | 3.429 |
����͓�̌Q�̔�r�E�E�E���R�xk��n-1=1
�n1��a�ώ@�x���̑��a=15
�d1��a���ғx���̑��a=8.549
�n2��b�ώ@�x���̑��a=20
�d2��b���ғx���̑��a=26.451
���蓝�v�ʃ�^2��6.441
��^2�i1,0.95�j=3.8415
�̂ɋA�����������p���Η��������̑�����ia,b�̍Ĕ����ɍ�������j
���B�x�m�F
�P�S�|�P�j���̃f�[�^����J�v�����}�C���[�@�ɂ�萶���m���𐄒肵�����Ȑ���`���C����AB�ɂ��Ⴂ�����邩���肹��
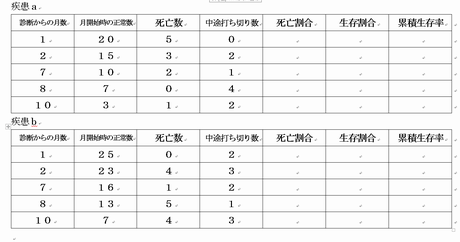
���ƌ�⑫
��15��@�܂Ƃ�
���B�ڕW�P�T�|�P���Ƃŏo������S�ĉ�����
�P�T�|�Q���C������v�����Ȋw�C����ӗ~������